 |
Операторы физических величин
|
|
|
|
Понятие волновой функции
Согласно гипотезе Луи де Бройля свободному движению любой частицы можно поставить в соответствие плоскую волну

где  - радиус-вектор произвольной точки пространства; t - время. Частота волны ω и волновой вектор
- радиус-вектор произвольной точки пространства; t - время. Частота волны ω и волновой вектор  связаны с энергией и импульсом частицы теми же соотношениями, что и для квантов света:
связаны с энергией и импульсом частицы теми же соотношениями, что и для квантов света:

где  - постоянная Планка.
- постоянная Планка.
Подставляя ω и  из (2) в (1), получаем выражение для волны де Бройля свободной частицы:
из (2) в (1), получаем выражение для волны де Бройля свободной частицы:

С другой стороны, атомизм частицы заключается в том, что она всегда действует как целое. Поэтому частица не может представлять собой образование из волн де Бройля.
Квантовая механика исходит из статистического толкования волн де Бройля, согласно которому
интенсивность волны де Бройля в какой-либо точке пропорциональна вероятности обнаружить частицу в этом месте пространства.
Состояние квантовой системы описывается волновой функцией ψ, которая в общем случае является комплексной функцией радиус-вектора  и времени t:
и времени t:  .
.
Физический смыслволновой функции заключается в том, что
вероятность нахождения частицы в момент времени в объеме  определяется формулой:
определяется формулой:

где  /в декартовой системе координат/.
/в декартовой системе координат/.
Так как нахождение частицы в пространстве - событие достоверное, то должно выполняться соотношение

где  - объем всего пространства.
- объем всего пространства.
Выражение (5) называется условием нормировки. Если интеграл от  сходится, то волновая функция всегда может быть нормирована соответствующим выбором постоянного коэффициента при ψ.
сходится, то волновая функция всегда может быть нормирована соответствующим выбором постоянного коэффициента при ψ.
Из условия (5) видно, что нормированная функция ψ определена с точностью до множителя, модуль которого равен единице, т. е. с точностью до множителя  , где α - любая действительная, константа. Эта неоднозначность не отражается на физических результатах, так как математически все физические величины определяются выражениями, содержащими произведение ψ на комплексно сопряженную функцию ψ * например- (4).
, где α - любая действительная, константа. Эта неоднозначность не отражается на физических результатах, так как математически все физические величины определяются выражениями, содержащими произведение ψ на комплексно сопряженную функцию ψ * например- (4).
|
|
|
Следующим положением, лежащим в основе квантовой механики, является принцип суперпозиции, который формулируется следующим образом:
Если квантовая система может находиться в состояниях, которые описываются волновыми функциями ψ1 и ψ2, то она может находиться и в состояниях, описываемых произвольной линейной комбинацией этих функций:

где C1, С2 - любые, не зависящие от времени комплексные числа.
Из принципа суперпозиции следует, что уравнение, описывающее изменение волновой функции в пространстве и во времени, должно бытьлинейно относительно  .
.
Операторы физических величин
В общем случае под оператором  понимается правило,по которому с каждой из рассматриваемого класса функций U (
понимается правило,по которому с каждой из рассматриваемого класса функций U ( ) сопоставляется другая функция - V (
) сопоставляется другая функция - V ( ). Это правило символически записывается в виде умножения U(
). Это правило символически записывается в виде умножения U( ) на
) на  :
:

Под  может подразумеваться, например, умножение на
может подразумеваться, например, умножение на  , дифференцирование по координатам
, дифференцирование по координатам  , извлечение корня
, извлечение корня  и т.п.
и т.п.
Из всех возможных операторов для изображения физических величин в квантовой механике используется лишь класс так называемых линейных самосопряженных операторов, так как только они могут соответствовать физическим величинам.
Оператор  , называется линейным, если он обладает следующим свойством:
, называется линейным, если он обладает следующим свойством:
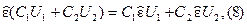
где U1, U2 - произвольные функции; С1, С2 - произвольные постоянные.
Необходимость этого свойства непосредственно вытекает из принципа суперпозиции; применение оператора не должно нарушать этот принцип.
Оператор  называется самосопряженным, или эрмитовым, если
называется самосопряженным, или эрмитовым, если

где интеграл берется по всей области возможного изменения  .
.
Значение введения операторов в квантовую механику заключаетсяв том, что все связи между физическими величинами могут быть выражены на языке операторов.
|
|
|
Основная идея применения операторов заключается в том, что с каждой физической величиной  /динамической переменной/ в квантовой механике сопоставляется изображающий ее линейный /чтобы выполнялся принцип суперпозиции/ и самосопряженный /чтобы значения были вещественны/ оператор
/динамической переменной/ в квантовой механике сопоставляется изображающий ее линейный /чтобы выполнялся принцип суперпозиции/ и самосопряженный /чтобы значения были вещественны/ оператор  .
.
Связь между операторами и измеряемыми динамическими переменными устанавливается с помощью выражения для среднего значения величины  , описываемой волновой функцией
, описываемой волновой функцией  :
:

Так как оператор  эрмитовый, это выражение может быть записано иначе:
эрмитовый, это выражение может быть записано иначе:

Используя правило (10), запишем выражение для отклонения от среднего значения в данном состоянии  :
:  и введем соответствующий эрмитов оператор:
и введем соответствующий эрмитов оператор:

Теперь можно записать выражение для среднего квадратичного отклонения:


которое, используя самосопряженность оператора  приведём к виду
приведём к виду

С помощью этого соотношения вычисляется среднее квадратичное отклонение физической величины в произвольном состоянии.
Чтобы найти такие состояния, при которых  имеет определенные значения, приравняем правую часть выражения (l4) нулю:
имеет определенные значения, приравняем правую часть выражения (l4) нулю:


Поскольку под интегралом стоит положительная величина, то из (15) следует  .
.
Модуль комплексного числа равен нулю, только когда само число равно нулю: 
Учитывая определение оператора  (12) и то, что в рассматриваемом состоянии
(12) и то, что в рассматриваемом состоянии  имеет определенное значение
имеет определенное значение  , окончательно находим
, окончательно находим 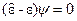 , или
, или  (16)
(16)
Так как  - оператор, соответствующий физической величине
- оператор, соответствующий физической величине  , то (16) представляет собой линейное уравнение для нахождения волновой функций
, то (16) представляет собой линейное уравнение для нахождения волновой функций  состояния, в котором эта величина имеет значение
состояния, в котором эта величина имеет значение  .
.
В квантовой механике оператор  часто является дифференциальным, т.е. содержит операцию дифференцирования. В этом случае (16) - линейное однородное дифференциальное уравнение.
часто является дифференциальным, т.е. содержит операцию дифференцирования. В этом случае (16) - линейное однородное дифференциальное уравнение.
В общем случае такое уравнение имеет нетривиальное /т.е. отличное от нуля/ решение только при некоторых определённых значениях Е, которые являются параметрами (16). Эти значения параметра  называются собственными значениями оператора
называются собственными значениями оператора  . Соответствующиеим решения (16)
. Соответствующиеим решения (16)  называются собственными функциями оператора
называются собственными функциями оператора  .
.
Параметры n, нумерующие собственные значения и собственные функции, называются квантовыми числами.
|
|
|
Совокупность собственных значений оператора называется его спектром.
Если оператор имеет дискретные собственные значения, такой спектр называется дискретным. В этом случае говорят, что величина имеет квантованные значения.
Если собственные значения пробегают непрерывный ряд значений, такой спектр его значений называется непрерывным.
Существуют такие состояния физической системы, которые описываются различными собственными функциями некоторого оператора, но соответствуют одному и тому же собственному значению. Такие состояния системы называются вырожденными, а число независимых собственных функций, соответствующих одному и тому же значению оператора, - краткостью вырождения.
Итак, мы определили, что
в состоянии, описываемом собственной функцией  оператора
оператора  , физическая величина имеет значение, равное собственному значению этого оператора.
, физическая величина имеет значение, равное собственному значению этого оператора.
В этом и заключается физическая интерпретация математического формализма квантовой механики.
Явный вид некоторых операторов не релятивистской квантовой механики приведен в таблице.
| Физическая величина | Оператор | ||
Координата 
| 
| ||
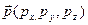
| 
| ||
Кинетическая энергия 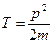
| 
| ||
Потенциальная энергия 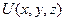
| 
| ||
Полная энергия 
| 
|
|
|
|


