 |
Свойства собственных функций операторов
|
|
|
|
Собственные функции операторов квантовой механики обладают следующими общими свойствами.
1. Если оператор  имеет дискретный спектр собственных значений
имеет дискретный спектр собственных значений  , то собственные функции этого оператора
, то собственные функции этого оператора  удовлетворяют уравнению
удовлетворяют уравнению

Уравнение, комплексно сопряжённое (18) для квантового числа m,

Умножаем (18) и (19) слева на  и
и  соответственно, интегрируем по всей области пространства и вычитаем из первого второе. В результате получаем
соответственно, интегрируем по всей области пространства и вычитаем из первого второе. В результате получаем 
Отсюда следует 
при n 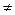 m - условие ортогональности собственных функций, соответствующих разным собственным значениям оператора.
m - условие ортогональности собственных функций, соответствующих разным собственным значениям оператора.
Физический смысл ортогональности собственных функций заключается в том, что
при измерении физической величины с достоверностью получается значение  в состоянии
в состоянии  и
и  - в состоянии
- в состоянии  .
.
Кроме того, в соответствии с (15) функции дискретного спектра всегда могут быть нормированы на единицу:

Соотношения (20) и (21) могут быть объединены:

гдесимвол Кронекера  определяется следующим образом:
определяется следующим образом:

| { | 1, если n = m; | (23) |
0, если n 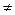 m. m.
|
Набор функций  удовлетворяющий условию (22), называется системой ортонормированных функций, т.е. ортогональных и нормированных.
удовлетворяющий условию (22), называется системой ортонормированных функций, т.е. ортогональных и нормированных.
2. Второе свойство собственных функций операторов заключается в том, что их совокупность образует полную систему функций. Это значит, что
любая функция  , определенная в той же области переменных, что и собственные функции
, определенная в той же области переменных, что и собственные функции  , может быть представлена в виде ряда
, может быть представлена в виде ряда

где суммирование выполняется по всем значениям квантового числаn.
Чтобы найти коэффициенты разложения  , умножим(24) слева на
, умножим(24) слева на  и проинтегрируем по всему пространству:
и проинтегрируем по всему пространству:

Меняя индексы m на n, получаем выражение для коэффициентов разложения:

Умножим(24) на комплексно сопряженное выражение
|
|
|

и проинтегрируем по всему пространству:

или 
Соотношение (27) - критерий того, что система функций  нормирована на единицу. Таким образом, в соответствии с (4)
нормирована на единицу. Таким образом, в соответствии с (4)
вероятность нахождения физической величины в состоянии со значением  равна квадрату модуля коэффициента
равна квадрату модуля коэффициента  в разложении (24), т.е. определяется интенсивностью
в разложении (24), т.е. определяется интенсивностью  , с которой собственное состояние
, с которой собственное состояние  представлено в состоянии
представлено в состоянии  .
.
Уравнение Шрёдингера
Основное уравнение квантовой механики - уравнение Шредингера, определяющее изменение волновой функции, т.е. состояния системы, в пространстве и времени:

где  - оператор Гамильтона системы; i - мнимая единица.
- оператор Гамильтона системы; i - мнимая единица.
Это уравнение - основное уравнение динамики в квантовой механике, поскольку позволяет найти волновые функции в любой момент времена, если известны вид оператора  и начальные условия.
и начальные условия.
Гамильтониан  /в отсутствие магнитного поля/ имеет вид (17) в уравнение Шредингера (28) может быть записано явно:
/в отсутствие магнитного поля/ имеет вид (17) в уравнение Шредингера (28) может быть записано явно:

В случае стационарного, т.е. не изменяющегося во времени, внешнего поля  гамильтониан не зависит от времени
гамильтониан не зависит от времени  . В этом случае в (29) переменные могут быть разделены:
. В этом случае в (29) переменные могут быть разделены:

Подставляя решения в виде (30) в (29) и обозначая постоянную разделения E, находим

Отсюда следуют два уравнения для T и 


Первое уравнение решается сразу:  , a второе является уравнением для собственных функций гамильтониана
, a второе является уравнением для собственных функций гамильтониана  . Таким образом, если система имеет дискретный спектр энергии, то решение (30) имеет вид
. Таким образом, если система имеет дискретный спектр энергии, то решение (30) имеет вид

т.е. гармонически зависит от времени с частотой  :
:

где  - собственное значение гамильтониана
- собственное значение гамильтониана  .
.
Волновые функции  , являющиеся решениями уравнения (32), соответствуют состояниям системы, в которых энергия имеет определенные значения. Такие состояния системы называются стационарными,а (32) поэтому называется стационарным уравнением Шредингера.
, являющиеся решениями уравнения (32), соответствуют состояниям системы, в которых энергия имеет определенные значения. Такие состояния системы называются стационарными,а (32) поэтому называется стационарным уравнением Шредингера.
Его явный вид

Стационарные уровни энергии  нумеруются, как правило, в порядке возрастания их абсолютного значения.
нумеруются, как правило, в порядке возрастания их абсолютного значения.
|
|
|
Стационарное состояние с наименьшим из всех возможных значений энергии называется основным.
Волновые функции, являющиеся решениями уравнения Шредингера (29), должны обладать следующими свойствами:
1. Волновые функции должны быть однозначны, непрерывны и конечны во всей области пространства. Эти требования должны также выполняться, когда потенциал U имеет поверхности разрыва. Необходимость однозначности и конечности волновой функции достаточно очевидна из ее физического смысла /см. (4) и (5)/: вероятность местонахождения частицы должна быть величиной конечной и однозначной. Кроме того, так как волновая функция является решением дифференциального уравнения вида (29), то она должна быть неразрывна, а также иметь однозначную, непрерывную и конечную первую производную.
2. Если существуют области пространства, где  , то в них везде
, то в них везде  . Частица, очевидно, не может находиться внутри этих областей. Непрерывность
. Частица, очевидно, не может находиться внутри этих областей. Непрерывность  требует, чтобы на границе этой области
требует, чтобы на границе этой области  . Производные от
. Производные от  на границе могут иметь разрыв.
на границе могут иметь разрыв.
|
|
|


