Задача №4 «Определение оптимальной стоимости величины транспортной партии груза и продолжительности производственного цикла.

 

Задание. Предприятие за время производственного цикла выпускает i=1…n видов продукции (на каждое назначение доставляет один вид продукции). Каждый i-й потребитель получает продукцию строго по норме в количестве Qi. За время производственного цикла Тп предприятие изготовляет продукцию и формирует транспортные партии q_i на все назначения.

Процессы производства, накопления продукции на транспортную партию (заказ) и ее отправление синхронизированы. Такой высокий уровень согласования между производством и транспортом отвечает главному принципу логистики – доставка груза «точно в срок» и значительному сокращению запасов готовой продукции. Данная модель является не единственной, описывающей рассматриваемые процессы. Характер производства, накопления и потребления готовой продукции равномерный.

Необходимо:

- определить оптимальные значения параметров q_i*,Тп*;

- построить и проанализировать графики зависимостей продолжительности производственного цикла от параметров указанных в задании.

 

Исходные данные:

Таблица 4

Производственная мощность предприятия по выпуску i-го вида продукции	Q1
Q2
Q3
Тариф на поставку транспортной партии i-му потребителю	f1
f2
f3
Стоимость хранения единицы i-го изделия	Cx1
Cx2	2,5
Cx3	1,6
Затраты предприятия	Cз
Построить зависимость Тп* от параметров	Q2,f1

 

Решение. В основу решения производственно-транспортной задачи положен принцип системного подхода. Он находит свое отражение во взаимодействии всех элементов логической цепи (ЛЦ): производства, транспорта и потребления, что, как известно, отвечает основополагающей концепции логистики.

При рассмотрении работы производственно-транспортной системы необходимо согласовать производственные (продолжительность производственного цикла предприятия) и транспортные (величина транспортной партии груза) параметры таким образом, чтобы затраты всей ЛЦ были минимальными. Таким образом, необходимо определить такие значения параметровq* и Тп*, которые бы дали минимум целевой функции затрат R(q_i,Тп). Функция R(q_i,Тп) выражает приведенные расходы по изготовлению, хранению, транспортировке и потреблению готовой продукции. Приведенные затраты зависящие от параметра Тп описываются выражением:

 

(15)

 

где ∑Сх_i – стоимость хранения единицы груза (изделия) при

накоплении на транспортную партию;

∑Спр – затраты предприятия отнесенные к производственному

циклу по выпуску транспортных партий заказов;

∑Ст_i – затраты по транспортировке груза.

 

Функция затрат при более полном описании слагаемых выражения (15) примет вид:

 

(16)

 

где Qп – производственная мощность предприятия, ед;

сх_i – стоимость хранения единицы груза (изделия) при накоплении

на транспортную партию, ден.ед.;

f_i – расходы на доставку партии груза i-му потребителю, ден.ед.;

Тп – продолжительность производственного цикла предприятия по

выпуску i-тых видов продукции, сут;

с_з – затраты предприятия отнесенные к производственному циклу

по выпуску i-тых транспортных партий заказов, ден.ед.

По условию задачи, соблюдая принцип логистики, величину затрат необходимо минимизировать: R(Тп)→min.

Условие минимизации затрат при определении оптимального значения Т*п выполняется путем решения уравнения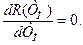

Решая данное уравнение, после преобразований получим:

 

(17)

 

 

 

Величину оптимальной транспортной партии определяем из соотношения:

 

qi* = Qi∙Тп* (18)

 

q₁ = 0,51∙300 = 153

q₂ = 0,51∙425 = 216,75=216,8

q₃ = 0,51∙185 = 94,35=94,4

 

Q2	Тп		f1	Тп
	0,510			0,510
	0,454			0,520
	0,411			0,529
	0,377			0,539
	0,349			0,547
	0,328			0,555
	0,308			0,564

 

Тп

 

 

Q₂

Тп

 

f₁

 

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: