 |
Тема 1 : Предел. Непрерывность. Частные производные
|
|
|
|
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
1.1. Определение функции нескольких переменных
Остановимся, в основном, на случае функции двух переменных. Определения и полученные результаты легко распространить и на случай большего числа переменных.
Рассмотрим плоскость О ху - множество всех точек 
.
Определение 1. Множество всех точек , координаты которых удовлетворяют неравенству 
, называется 
-окрест-ностью точки 
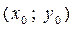и обозначается 
.
Определение 2. Областью D называется множество точек, обладающих свойствами:
1. Любая точка 
принадлежит ей и вместе с некоторой 
- окрестностью (свойство открытости);
2. Любые точки 
и 
можно соединить непрерывной линией, целиком принадлежащей D (свойство связности).
Линия, ограничивающая данную область, называется границей. Если к области отнести и точки границы, то такая область называется замкнутой.
D
М 1 М 2
Определение 3. Если каждой паре значений двух независимых переменных из некоторой области D соответствует по некоторому правилу или закону определённое значение величины z, то z называется функцией двух переменных в области D, и пишут 
.
Аналогично, как и для функции одной переменной определяется многозначная функция нескольких переменных.
Пример 1. Закон Ома: 
- функция двух переменных.
Пример 2. Работа постоянной силы на прямолинейном перемещении: 
- функция трёх переменных.
Определение 4. Множество значений , при которых определена , называется областью определения функции.
Пример 3. Найти область определения функций:
1. 
, т.е. областью определения данной функции является круг 
.
2. 
, т.е. область определения - первая и третья координатные четверти без координатных осей.
|
|
|
Геометрически функцию двух переменных можно представить как поверхность, уравнение которой 
. Например, уравнение функции 
геометрически представляет параболоид.
1.2. Предел и непрерывность функции двух переменных
Точка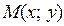 
стремится к точке 
, если расстояние между этими точками стремится к нулю, т.е. 
. Это очевидно эквивалентно: 
.
Определение 5. Число А называется пределом функции при стремлении точки 
, если 
, для всех точек из которой выполняется неравенство 
, и пишут
или 
.
Аналогично устанавливается понятие о бесконечном пределе функции. В случае, когда 
или 
, неравенство заменяется неравенствами вида: 
или 
соответственно, где М - произвольное положительное число, и пишут
или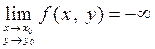 
.
Определение 6. Функция имеет пределом число А при 
и 
если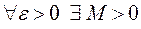 
, что 
при 
и пишут
.
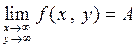Определение 7. Функция называется непрерывной в точке М 0, если имеет место равенство
.
Если в некоторой точке условие непрерывности не выполняется, такая точка называется точкой разрыва.
Пример 4. Исследовать на непрерывность функцию 
в точке 
Рассмотрим значения функции вдоль прямых 
при
.
Таким образом, функция принимает разные значения в зависимости от значения k. Точка 
является точкой разрыва.
Замечание. Свойства непрерывной функции двух переменных аналогичны соответствующим свойствам функции одной переменной.
1.3. Частные производные функции двух переменных
Дадим независимой переменной х приращение 
, тогда функция 
получит приращение, которое называется частным приращением z по х и обозначается
.
Аналогично определяется частное приращение z по у:
.
Если же приращение получают одновременно х и у, то приращение
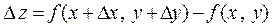
называется полным.
Определение 8. Частной производной от функции по х называется предел
,
или другие обозначения: 
.
Аналогично, 
,
или 
.
Из этих определений следует, что правила вычисления частных производных совпадают с правилами для функции одного переменного. При этом, например, если мы вычисляем производную 
, то в процессе дифференцирования считаем, что 
|
|
|
Пример 5. Найти и 
, если 
1.4. Полный дифференциал функции двух переменных
Как известно, полное приращение функции определяется по формуле 
. Пусть имеет непрерывные частные производные, т.е. является дифференцируемой. Полное приращение представим в виде
.
К каждой разности применим теорему Лагранжа
,
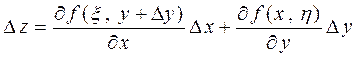где 
.
Так как в силу непрерывности существуют пределы:
; 
,
то по теореме о пределе функции получим
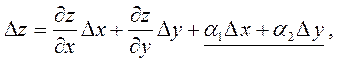
где 
.
Это означает, что подчеркнутое слагаемое является б.м.в. при 
и тогда
,
где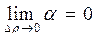 
.
Таким образом, получаем еще одно эквивалентное определение дифференцируемой функции двух переменных.
Определение 8. Функция называется дифференцируемой в точке, если её приращение можно представить в виде суммы двух слагаемых, линейных относительно 
и 
и величины бесконечно малой. высшего порядка относительно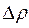 
, т.е.
При этом линейная часть 
называется полным дифференциалом и обозначается
Так как приращения независимых переменных называются их дифференциалами, то окончательно
а 
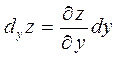- частные дифференциалы.
1.5. Производная сложной функции
Пусть задана функция 
, где 
. В этом случае z является сложной функцией аргументов х и у. Пусть все эти функции имеют непрерывные частные производные.
Дадим переменной х приращение , тогда
где 
.
Разделим данное равенство на 
и перейдём к пределу при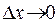 
Отсюда следует 
.
Аналогично получим 
.
Пример 6. Найти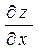 
и , если 
|
|
|
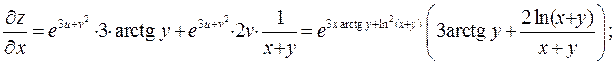
