 |
Лекция № 33. Тема 2 : Частные производные.
|
|
|
|
Производная по направлению. Градиент
2.1. Полная производная
Пусть дана функция 
, где 
. Тогда, обобщая формулу для случая производной функции двух переменных, получаем
. (1)
Формула (1) называется формулой полной производной.
Пример 1. Найти полную производную функции 
, если 
.
.
2.2. Частные производные функции, заданной неявно
Требуется найти частные производные 
и 
, если 
, где 
. Воспользуемся правилом дифференцирования сложной функции для случая трёх переменных
.
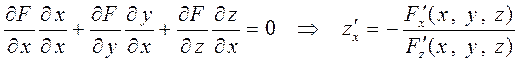Аналогично находим 
.
Замечание 1. Отсюда следует ранее рассмотренный случай для функции одной переменной: Если 
, где 
.
Пример 2. Найти частные производные функции, заданной неявно
.
2.3. Частные производные высших порядков
Рассмотрим функцию 
. Если частные производные 
и 
являются дифференцируемыми функциями, то от них можно снова находить частные производные. Частные производные второго порядка определяются следующим образом
Последние две производные называются смешанными производными второго порядка.
Аналогично определяются производные высших порядков. Например,
- означает, что функция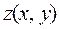 
сначала дифференцируется т раз по х, а затем п - т раз по у.
Пример 3. Найти смешанные производные второго порядка функции 
.
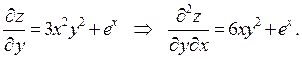
Получено равенство двух смешанных производных второго порядка. Зависит ли в общем случае результат дифференцирования от порядка дифференцирования?
Теорема. Если функция 
и ее частные производные 
определены в некоторой окрестности точки М и 
непрерывны, то в этой окрестности смешанные производные равны
.
2.4. Производная по направлению
Рассмотрим функцию трёх переменных , заданную в некоторой пространственной области z 
|
|
|
V и точку 
. V
Проведём из точки М вектор , 
направляющие косинусы которого M
. На векторе 
возьмём точку 
, y
тогда 
-
расстояние между точками М и М 1. x
Приращение функции будет иметь вид
,
где 
. Если разделить это равенство на 
и перейти к пределу при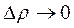 
, то получим
. (1)
Формула (1) представляет собой производную функции 
по направлению вектора .
Замечание 2. Частные производные – это частный случай производных по направлению векторов: 
.
Замечание 3. На плоскости производная по направлению имеет вид
.
Пример 4. Найти производную по направлению в точке 
от функции 
по направлению вектора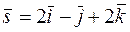 
.
Вычислим частные производные в точке М:
Определим направляющие косинусы вектора :
.
Тогда 
.
2.5. Градиент функции
Рассмотрим функцию трёх переменных.
Определение 1. Совокупность точек, удовлетворяющих уравнению 
, где 
, образует поверхность, которая называется поверхностью уровня.
Пример 5. Найти поверхности уровня функции 
.
Замечание 4. Для функции двух переменных имеем уравнения линии уровня 
.
Определение 2. Вектор 
называется гради-ентом функции 
.
Замечание 5. Для функции двух переменных градиент имеет вид 
.
Основные свойства градиента:
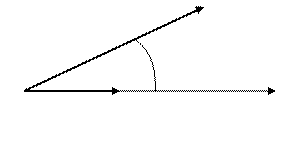1. Производная по направлению 
равна проекции 
на , т.е. 
.
Так как единичным вектором 
для вектора будет вектор
, 
то
что и требовалось доказать.
2. Производная по направлению в данной точке имеет наибольшее значение, если направление вектора совпадает с направлением градиента.
Это следует из свойства 1, так как 
будет при 
.
3. Производная по направлению, перпендикулярному градиенту, равна нулю. Это свойство также следует из свойства 1, так как
4. Градиент направлен перпендикулярно к поверхности уровня.
Пример 6. Найти градиент функции 
в точке 
.
Находим частные производные:
Тогда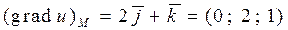 
.
Лекция № 34
2.6. Касательная и нормаль к поверхности
|
|
|
Пусть поверхность задана уравнением . Это уравнение можно рассматривать как уравнение поверхности уровня функции 
при 
, и тогда нормаль
на основании свойств градиента
получаем уравнение нормали
в точке 
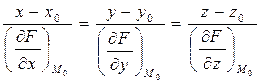Р
и уравнение касательной плоскости Р
Замечание 1. Если поверхность задана уравнением 
, то её можно представить в виде
и тогда уравнение нормали
а уравнение касательной плоскости
.
Пример 1. Составить уравнения касательной плоскости и нормали к сфере 
в точке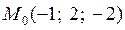 
.
Вычислим частные производные в этой точке:
Тогда получаем уравнение нормали
,
а уравнение касательной плоскости –
или 
.
Тема 3*: Векторная функция скалярного аргумента
3.1. Векторная функция. Предел. Непрерывность
Аналогично, как и для плоской линии, пространственная линия может быть задана параметрическими уравнениями вида
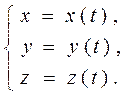
Например, 
– уравнения прямой в пространстве, а 
, где 
- уравнения винтовой линии (спираль).
Замечание 2. В механике под параметром t подразумевается время.
Рассмотрим радиус-вектор 
, координаты которого являются функциями параметра t
. (1)
Каждому значению параметра t по формуле (1) соответствует определённый вектор 
, т.е. является функцией скалярного аргумента t. Таким образом, векторная функция скалярного аргумента записывается в виде 
. z
Определение. Линия, описанная годограф
концом вектора 
, называется
годографом векторной функции
. 
Предел и непрерывность векторной 
y
функции определяется через скалярные х
функции 
.
Если существуют пределы:
то 
, где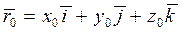 
.
Аналогично определяется непрерывность векторной функции через непрерывность функций .
3.2. Производная векторной функции
Дадим приращение аргументу t. В результате векторная функция получит приращение
Рассмотрим отношение 
. Если функции являются дифференцируемыми, то
. (2)
Формула (2) определяет производную векторной функции скалярного аргумента. Модуль этого вектора равен
.
Выясним геометрический смысл производной.
М 
М 1
О 
Из рисунка видно, что при 
, т.е. производная имеет направление касательной. Нормалей к пространственной кривой в данной точке можно провести бесконечное множество – все они лежат в плоскости, которая называется нормальной плоскостью. Исходя из геометрического смысла производной, получаем уравнение касательной
|
|
|
и уравнение нормальной плоскости
.
Замечание 3. Из определения производной следует, что правила её нахождения такие же, как и для скалярной функции одного переменного.
Аналогично, как и для плоской линии, вводится понятие её кривизны.
Формула для вычисления кривизны пространственной линии имеет вид
.
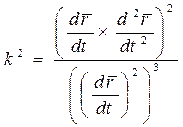Пример 2. Показать, что если 
то 
Действительно, так как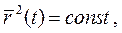 
то дифференцируя, получаем 
, ч.т.д.
Пример 3. Составить уравнение касательной, нормальной плоскости и вычислить кривизну винтовой линии в точке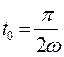 
.
Вычислим значения функций и их производных в соответствующей точке:
Составим уравнение касательной
и нормальной плоскости
Найдём векторное произведение векторов 
Тогда
.
|
|
|
