 |
Скорость перемещения ионов в электрическом поле.
|
|
|
|
Скорость перемещения ионов в электрическом поле.
Между плотностью потока ионов, движущихся под действием элетрического поля, и скоростью движения каждой частицы существует очень простая зависимость. Чтобы её получить, обратимся к рис. 8.

Рис. 8. Связь между величиной плотности потока J и скоростью движения каждой частицы v.
Поскольку каждую секунду через площадь S проходит Ф = vSС киломолей частиц (С-молярная концентрация), то поток Ф = vSС, а плотность потока равна: J = vС.
Предположим через некую плоскость S ионы движутся в направлении X под действием электрического поля. За одну секунду каждый ион проходит расстояние 1v, м, где v . скорость перемещения иона, м/с. Отложив это расстояние влево от плоскости S, мы получим объём 1vS, в котором содержится 1vSn частиц, или 1vSС киломолей вещества. Это количество вещества и переносится за секунду через плоскость S. Таким образом, поток равен:
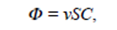 (7)
(7)
а плотность потока равна произведению скорости перемещения частиц на их молярную концентрацию:
 (8)
(8)
Смысл этого уравнения тоже довольно прост: поток пропорционален концентрации ионов и их скорости движения в электрическом поле.
 (9)
(9)
Мы получили основное уравнение элетрофореза, справедливое как для ионов, «случайно прыгающих» в мембране, так и для макроскопических тел, плавно плывущих в электрическом поле. Его смысл уж совсем очевиден: скорость движения частиц в электрическом поле пропорциональна приложенной к ней силе и величине, которую называют (электрофоретической) подвижностью.
Между электрофоретической подвижностью и коэффициентом диффузии существует прямая пропорциональность
 (10)
(10)
Введение величины электрофоретической подвижности позволяет несколько упростить выражения в уравнении электрофореза:
|
|
|
 (11)
(11)
а вместе с тем изменить форму написания основного электродиффузионного уравнения:
 (12)
(12)
Это уравнение известно под названием уравнения Нернста-Планка.
Закон Фика для диффузии молекул в сплошной среде:
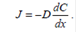 (13)
(13)
Сравнение этого уравнения с уравнением Фика для диффузии (13) и уравнением электрофореза (7) показывает, что суммарный поток в случае электродиффузии складывается алгебраически из диффузионного и электрофоретического потоков; иными словами,
диффузионное и электрофоретическое движение ионов происходят независимо друг от друга.
Уравнение Теорелла
Электродиффузионное уравнение показывает, что два градиента являются движущей силой потока ионов: градиент концентрации и градиент потенциала. Эти две величины: концентрация и потенциал, . являются главными составляющими энергии иона в среде, в том числе в липидной фазе мембраны, или, другими словами. составляющими электрохимического
потенциала. Из сказанного ясно, что градиент электрохимического потенциаладолжен определять величину потока ионов. Чтобы убедиться в том, что это действительно так, продифференцируем величину μ (электрохимический потенциал иона) по координате х в
направлении движения:
 (13-16)
(13-16)
основное уравнение электродиффузии:
 (17-18)
(17-18)
Это уравнение Теорелла.
Его смысл достаточно ясен и интуитивно понятен: поток равен
произведению концентрации ионов, подвижности ионов и обратному градиенту электрохимического потенциала. Последнюю величину с полным основанием можно назвать движущей силой потока. В заключение добавим, что хотя мы вывели уравнеие для частного случая однородной среды, они справедливо и в том случае, если среда неоднородна, т. е.
имеется ненулевой градиент химического сродства (dμ 0/dt ≠ 0).
|
|
|
|
|
|


