Эластичность спроса по цене.

ластичность – безразмерная величина, значение которой не зависит от ­того, в каких единицах мы измеряем цены, объем или другие величины.

Эластичность спроса (E_d) – это чувствительность спроса к изменению одной из его переменных, определяемая как отношение процентного изменения величины спроса к процентному изменению переменной.

Различают эластичность спроса по цене, эластичность спроса доходу и перекрестную эластичность.

Эластичность спроса по цене (Е^p_d) – это чувствительность спроса к изменению цены, определяемая как отношение процентного изменения величины спроса к процентному изменению цены.

На рис. 22 представлены две кривые спроса, в первом случае изменения цены с 7 до 4 руб. не привело к резкому увеличению спроса (Е_d=0,3), во втором случае спрос резко возрос (Е_d=1,22).

 

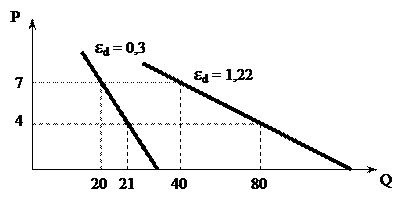
Рисунок 22 – Эластичность спроса по цене

Неэластичный спрос – это спрос, объем которого изменяется незначительно при изменении цены.

Эластичный спрос – это спрос на товар, объем которого изменяется существенно при изменении цены.

Итак, эластичность спроса по цене (E^p_d) показывает степень воздействия изменения цены на изменение количества продукции, на которую предъявлен спрос.

Эластичность определяется как отношение процентного изменения объема спроса к процентному изменению цены.

Коэффициент эластичности спроса по цене, как правило, является отрицательной величиной, так как с ростом цены объем спроса падает, но в экономической теории принято пользоваться абсолютным значением этого показателя, поэтому знак «минус» порой не ставят, но при расчетах принимают во внимание.

Коэффициент эластичности показывает, на сколько процентов меняется объем спроса на товар в результате изменения его цены на 1%.

Например, Е^р_d = -2. Это означает, что снижение цены (рост) на 1% приводит к росту (снижению) объема спроса на 2%.

Эластичности взаимно обратных функций являются взаимообратными величинами:

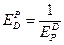
где E^P_d – коэффициент эластичности спроса по цене,

Е^d_P – коэффициент эластичности цены по спросу.

Поясним вышеизложенное на примере.

Пусть эластичность спроса по цене равна -0,6 (снижение цены на 1% приведет к росту объема спроса на 0,6%). Определим коэффициент эластичности цены по спросу:

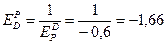– это означает, что рост объема спроса на 1% приведет к кипению цены на 1,66%

Эластичность линейной функции спроса изменяется от 0 до -∞.

Различают пять типов эластичности:

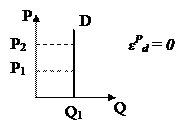
1) Совершенно эластичный спрос – объем спроса не изменяется при любом изменении цены, например, спрос на продукты питания (). Это типично для мгновенного равновесия. В этом случае функция спроса представлена в виде – Q^D=a.

2) Неэластичный спрос – значение ценовой эластичности меньше единицы и изменяется в пределах 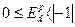. Объем спроса в процентах изменяется медленнее, чем изменяется цена в процентах, т.е. при изменении цены на 1% величина спроса изменяется менее чем на 1%. Эта ситуация характерна для мгновенного равновесия, кривая спроса будет представлена уравнением – Q^D=a – Р.

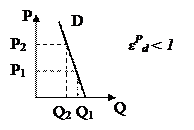
3) Единичная эластичность – при изменении цены величина проса меняется на ту же величину, т.е. при изменении цены на 1% величина спроса меняется на 1% ().

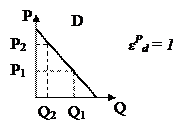
4) Эластичный спрос – значение ценовой эластичности больше единицы и изменяется в пределах 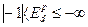. Объем спроса в процентах изменяется быстрее, чем изменяется цена в процентах, т.е. при изменении цены на 1% величина спроса изменяется более чем на 1% (). Это характерно для длительного равновесия и кривая представлена следующим образом – Q^D=a – Р∙b.

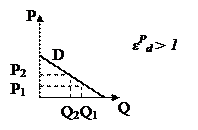
5) Бесконечно эластичный спрос – объем спроса может меняться до бесконечности при незначительном изменении цены, например, повышение спроса при повышении дохода ().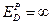

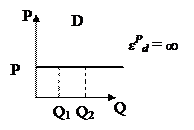
На степень эластичности спроса влияет целый ряд факторов:

1) наличие заменителей: чем больше товаров-субститутов, тек эластичней спрос на данный товар;

2) удельный вес товара в бюджете потребителя: чем выше удельный вес, тем выше ценовая эластичность;

3) размер дохода;

4) вид товара: является ли товар предметом роскоши (спрос и такие товары эластичен) или предметом первой необходимости (спрос на них неэластичен);

5) размер запаса: чем больше запас, тем более эластичен спрос;

6) рассматриваемый период: в краткосрочном периоде благо неэластично, в долгосрочном – эластично. Например, в краткосрочном периоде потребление электроэнергии неэластично, так как мы можем быстро отказаться от имеющихся электроприборов, а в долгосрочном – довольно эластично, поскольку мы будем заменять электроемкие приборы более экономичными.

Различают точечную и дуговую эластичность – при небольших изменениях цены или объема спроса или в случае вычисления эластичности в конкретной ситуации (точке) используется формула точечной эластичности, а при значительных – дуговой эластичности

Дуговая эластичность – это показатель средней реакции объема спроса на изменение цены товара на некотором отрезке D₁D₂ (рис. 22). Ее определяют с учетом средней точки.

 

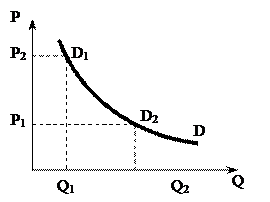
Рисунок 22 – Графическая интерпретация дуговой эластичности спроса

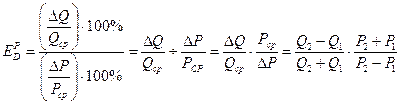
Точечная эластичность – характеризует относительное изменение одного фактора, например, объем спроса, при бесконечно малом изменении другого, напрмер, цены.

Для ее расчета используют следующие формулы:

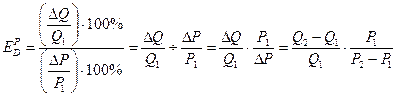
или, взяв производную от функции спроса:

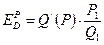
где 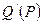– производная функции спроса по цене,

P₁ – цена в конкрет­ной точке,

Q₁ – объем спроса в конкретной точке.

Точечную эластичность можно определить и графическим способом, если провести касательную к кривой спроса в искомой точке. Наклон кривой спроса в любой точке определяется значением тангенса угла касательной с осью ОХ (рис. 23). Ошибочно считают, что значение точечной эластичности обратно пропорционально тангенсу угла наклона α, в формуле точечной эластичности только значение (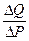) обратно пропорционально тангенсу угла наклона α.

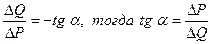
Рисунок 23 – Графическая интерпретация точечной эластичности

Наклон кривой спроса будет постоянным на всем ее протяжении идентифицирован в виде ценового коэффициента b (кривая спроса задается линейной функцией Q^D=a – Р∙b) который является величиной обратной наклону кривой спроса, т.е.

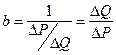
Подставим это выражение в классическую формулу точечной эластичности и получим:

⇐ Предыдущая45678910111213Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: