 |
Элементы теории вероятностей
|
|
|
|
РАЗДЕЛ 3
ИНТЕГРАЛЬНОЕ ИЧИСЛЕНИЕ
1.С ГЕОМЕТРИЧЕСКОЙ ТОЧКИ ЗРЕНИЯ НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ-ЭТО:
1. семейство кривых;
2. скорость изменения функции;
3. площадь криволинейной трапеции;
4. тангенс угла наклона касательной к графику функции в этой точке.
2.ИНТЕГРИРОВАНИЕ МЕТОДОМ ЗАМЕНЫ ПЕРЕМЕННОЙ ПРЕДПОЛАГАЕТ:
1. замену подынтегрального выражения на произведение;
2. замену интеграла от сложной функции на произведение двух интегралов;
3. ввод промежуточной переменной интегрирования.
4. замену подынтегрального выражения на сумму;
3.ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА ОПРЕДЕЛЯЕТ:
1. значение неопределенного интеграла;
2. значение определенного интеграла;
3. значение производной;
4. значение дифференциала.
4.ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ ИСПОЛЬЗУЕТСЯ ДЛЯ ВЫЧИСЛЕНИЯ:
1. скорости роста популяции;
2. площади криволинейной трапеции;
3. скорости изменения температуры в системе;
4. скорости движения тела.
5.ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЕМ НАЗЫВАЮТ УРАВНЕНИЕ ВИДА:
1.  ;
;
2.  ;
;
3.  ;
;
4.  .
.
6.ПОРЯДОК ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ-ЭТО:
1. наименьший порядок производной функции;
2. наивысший порядок степени аргумента;
3. наивысший порядок производной функции;
4. наименьший порядок степени аргумента.
7.ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ-ЭТО УРАВНЕНИЕ, СОДЕРЖАЩЕЕ:
1. независимую переменную и ее степень любого порядка;
2. независимую переменную, функцию и ее степень любого порядка;
3. функцию и независимую переменную;
4. функцию, независимую переменную и производную функции любого порядка.
8.ЧАСТНОЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ПОЛУЧАЮТ ПРИ:
1. подстановке конкретного значения постоянной C в уравнение;
|
|
|
2. подстановке заданных начальных значений х0 и y0 в уравнение;
3. подстановке в общее решение заданных начальных значений х0 и y0;
4. подстановке общего решения в уравнение.
9.ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЕМ С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ НАЗЫВАЮТ УРАВНЕНИЕ ВИДА:
1.  ;
;
2. 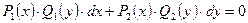 ;
;
3.  .
.
4. 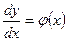 ;
;
РАЗДЕЛ 4.
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
1.СОБЫТИЯ НАЗЫВАЮТ СОВМЕСТИМЫМИ, ЕСЛИ:
1. наступление одного из событий не исключает появление другого,
2. наступление одного из них сопровождается наступлением другого,
3. в условиях опыта произойдут только эти события и никакие другие.
4. верны все варианты
2.СОБЫТИЯ НАЗЫВАЮТ ЕДИНСТВЕННО ВОЗМОЖНЫМИ:
1. если в условиях данного опыта произойдут только эти события и никакие другие,
2. если наступление одного из событий исключает появление другого,
3. если события не могут произойти одновременно в условиях данного опыта.
4. верны все варианты
3.ПОД ПРОТИВОПОЛОЖНЫМИ СОБЫТИЯМИ ПОНИМАЮТ:
1. два единственно возможных события образующих полную группу.
2. если наступление одного из событий исключает появление другого,
3. события, которые в результате опыта могут наступить, но могут и не наступить, при условии что эти события образуют полную группу.
4. верны все варианты
4.ВЕРОЯТНОСТЬЮ СОБЫТИЯ НАЗЫВАЕТСЯ:
1. отношение числа благоприятных исходов к общему числу возможных исходов
2. численная мера степени объективной возможности не появления этого события,
3. событие, если оно обязательно произойдет в условиях данного опыта.
4. верны все варианты
5.ВЕРОЯТНОСТЬ НАСТУПЛЕНИЯ СОБЫТИЙ, ОБРАЗУЮЩИХ ПОЛНУЮ ГРУППУ
РАВНА:
1.нулю
2.единице
3.разности между единицей и вероятностью наступления события А.
4. 0,5
6.ВЕРОЯТНОСТЬ ДОСТОВЕРНОГО СОБЫТИЯ РАВНА:
1. нулю
2. единице
3. разности между единицей и вероятностью наступлению события А.
4. 0.5
7.КЛАССИЧЕСКАЯ ВЕРОЯТНОСТЬ СОБЫТИЯ ЧИСЛЕННО РАВНА:
|
|
|
1. Р(А)= 
2. Р(А)=1-Р( )
)
3. Р(А)=lim  , при n
, при n 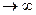
4. Р(А)=lim  ,
,
8.СТАТИСТИЧЕСКАЯ ВЕРОЯТНОСТЬ СОБЫТИЯ ЧИСЛЕННО РАВНА:
1. Р(А)=lim  , при n
, при n 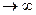
2. Р(А)=1-Р( )
)
3. Р(А)= 
4. Р(С)=Р(А)*Р(В)
9.СУММОЙ ДВУХ СОБЫТИЙ А И В ЯВЛЯЕТСЯ СОБЫТИЕ С, КОТОРОЕ ЗАКЛЮЧАЕТСЯ:
1. в появлении либо события А, либо события В,
2. в одновременном появлении событий А и В,
3. в исключении события А и события В.
4. верны все варианты
10.ПРОИЗВЕДЕНИЕМ ДВУХ СОБЫТИЙ А И В ЯВЛЯЕТСЯ СОБЫТИЕ С, КОТОРОЕ ЗАКЛЮЧАЕТСЯ:
1.в исключении события А и события В,
2.в появлении либо события А, либо события В,
3.в одновременном появлении события А и события В.
4. верны все варианты
11.ВЕРОЯТНОСТЬ СУММЫ ДВУХ СОВМЕСТИМЫХ СОБЫТИЙ РАВНА:
1. Р(А+В)=Р(А)+Р(В)
2. Р(А+В)=Р(А)+Р(В)-Р(АВ)
3. Р(А+В)=Р(А)+Р(В)+Р(АВ)
4. Р(А+В)=Р(А)*Р(В)
12.ВЕРОЯТНОСТЬ СУММЫ ДВУХ НЕСОВМЕСТИМЫХ СОБЫТИЙ РАВНА:
1. Р(А+В)=Р(А)+Р(В)-Р(АВ)
2. Р(А+В)=Р(А)+Р(В)+Р(АВ)
3. Р(А+В)=Р(А)+Р(В)
4. Р(А+В)=Р(А)*Р(В)
13.ВЕРОЯТНОСТЬ ПРОИЗВЕДЕНИЯ ДВУХ НЕЗАВИСИМЫХ СОБЫТИЙ РАВНА:
1. Р(А*В)=Р(А)*Р(В)
2. Р(А*В)=Р(А)*Р(В/А)
3. Р(А*В)=Р(А)*Р(В)*Р(В/А)
4. Р(А*В)=Р(А)+Р(В)
14.ВЕРОЯТНОСТЬ ПРОИЗВЕДЕНИЯ ДВУХ ЗАВИСИМЫХ СОБЫТИЙ РАВНА:
1. Р(А*В)=Р(А)*Р(В)*Р(В/А)
2. Р(А*В)=Р(А)*Р(В)
3. Р(А*В)=Р(А)*Р(В/А)
4. Р(А*В)=Р(А)+Р(В)
15.ФОРМУЛА БАЙЕСА ПОЗВОЛЯЕТ ОПРЕДЕЛИТЬ:
1.доопотные вероятности,
2.послеопотные вероятности гипотез
3.полную вероятность.
4. вероятность события
16.ЗНАМЕНАТЕЛЬ В ФОРМУЛЕ БАЙЕСА ЭТО:
1.доопотные вероятности,
2.послеопотные вероятности,
3.полная вероятность.
4. классическая вероятность
РАЗДЕЛ 5
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ.
1.ДИСКРЕТНОЙ НАЗЫВАЮТ ТАКУЮ СЛУЧАЙНУЮ ВЕЛИЧИНУ:
1. которая принимает некоторые значения из некоторого интервала,
2. которая принимает только отдельные числовые значения в определенном интервале,
3. значения которой можно просчитать.
4. нет правильного ответа
2.НЕПРЕРЫВНОЙ НАЗЫВАЮТ ТАКУЮ СЛУЧАЙНУЮ ВЕЛИЧИНУ:
1. которая принимает некоторые значения из некоторого интервала,
2. значения которой лежат в определенном интервале,
3. значения которой можно просчитать.
4. нет правильного ответа
3.ДИСПЕРСИЯ ХАРАКТЕРИЗУЕТ:
1.среднее значение случайной величины,
2.степень рассеяния случайной величины.
3.функцию распределения случайной величины.
|
|
|
4. нет правильного ответа
4.РАЗМЕРНОСТЬ ДИСПЕРСИИ ХАРАКТЕРИЗУЕТСЯ:
1. линейными единицами,
2. квадратными единицами,
3. безразмерными единицами.
4. нет правильного ответа
5.ДИСПЕРСИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ РАССЧИТЫВАЕТСЯ ПО ФОРМУЛЕ:

3. 
4. нет правильного ответа
6.ДИСПЕРСИЯ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ РАССЧИТЫВАЕТСЯ ПО ФОРМУЛЕ:
1. 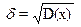
2. 
3. 
4. нет правильного ответа
РАЗДЕЛ 6
|
|
|


