 |
Законы распределения случайных величин
|
|
|
|
1.ДИСКРЕТНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА ПОДЧИНЯЕТСЯ:
1. распределению Пуассона,
2. нормальному распределению,
3. биноминальному распределению.
4. биноминальному распределению и распределению Пуассона,
2.БИНОМИНАЛЬНОЕ РАСПРЕДЕЛЕНИЕ ПРИМЕНЯЕТСЯ:
1.в случае редких событий,
2.если вероятность единичного события больше 0.1,
3.если заданное значение случайной непрерывной величины находится
в определенном интервале.
4. нет правильного ответа
3.РАСПРЕДЕЛЕНИЕ ПУАССОНА ПРИМЕНЯЕТСЯ ПРИ РАСЧЕТЕ ВЕРОЯТНОСТИ ТОГО, ЧТО ПРИ n ИСПЫТАНИЯХ НУЖНОЕ НАМ СОБЫТИЕ ПРОИЗОШЛО m РАЗ:
1. если вероятность единичного события больше 0.1
2. в случае редких событий,
3. если заданное значение непрерывной случайной величины лежит в
определенном интервале.
4. нет правильного ответа
4.В СЛУЧАЕ РЕДКИХ СОБЫТИЙ ПРИМЕНЯЕТСЯ:
1. биноминальное распределение,
2. нормальное распределение,
3. распределение Пуассона.
4. нет правильного ответа
5.ТЕМАТИЧЕСКИМ ОЖИДАНИЕМ СЛУЧАЙНОЙ ВЕЛИЧИНЫ НАЗЫВАЕТСЯ:
1. сумма произведений всех возможных значений случайной величины на их вероятности,
2. корень квадратной из дисперсии,
3. совокупность всех значений этой величины с соответствующими вероятностями.
4. нет правильного ответа
6.МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ РАССЧИТЫВАЕТСЯ ПО ФОРМУЛЕ:
1. 
2. 
3. 
4. нет правильного ответа
7.МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ НЕПРЕРЫВНОЙСЛУЧАЙНОЙ ВЕЛИЧИНЫ РАССЧИТЫВАЕТСЯ ПО ФОРМУЛЕ:
1. 
2. 
3. 
4. нет правильного ответа
8.БЕРИТЕ ФОРМУЛУ, СООТВЕТСТВУЮЩУЮ СРЕДНЕКВАДРАТИЧЕСКОМУ ОТКЛОНЕНИЮ:
1. 
2. 
3. 
4. нет правильного ответа
МОДУЛЬ 2.
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
|
|
|
РАЗДЕЛ 1.
БИОЛОГИЧЕСКАЯ СТАТИСТИКА
4. ГИСТОГРАММА ЭТО ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ ЗАВИСИМОСТИ:
1. значений функций распределения от значений случайной величины
2. функции плотности вероятности распределения от случайной величины
3. дисперсии от значений случайной величины
4. нет правильного ответа
2. ОСНОВНАЯ ЦЕЛЬ ТРЕТЬЕГО ЭТАПА СТАТИСТИЧЕСКОЙ РАБОТЫ ЗАКЛЮЧАЕТСЯ В:
1. расчете необходимого объема выборки,
2. оценке параметров генеральной совокупности по данным полученным на выборке,
3. обработке данных, полученных на выборке.
4. нет правильного ответа
4. РАЗМАХ ВЫБОРКИ ОПРЕДЕЛЯЕТСЯ ПО ФОРМУЛЕ:
1. 
2. 
3. Xmax-Xmin
4. 
4. НЕОБХОДИМЫЙ ОБЪЕМ ВЫБОРКИ ВЫЧИСЛЯЕТСЯ ПО ФОРМУЛЕ:
1. 
2. 
3. 
4. 
4. НОРМИРОВАННОЕ ОТКЛОНЕНИЕ ЗАВИСИТ:
1. от доверительной вероятности
2. от точности эксперимента
3. от среднего значения выборки
4. от объема выборки и доверительной вероятности
5. от объема выборки
6. КОЭФФИЦИЕНТ СТЬЮДЕНТА НАХОДЯТ ИЗ ТАБЛИЦЫ ПО ЗНАЧЕНИЯМ:
1.доверительной вероятности и среднего значения,
2.уровня значимости и среднеквадратического отклонения,
3 .доверительной вероятности и объема выборки,
4.доверительной вероятности и уровня значимости.
7.ЗАВИСИМОСТЬ НАЗЫВАЕТСЯ ФУНКЦИОННАЛЬНОЙ, ЕСЛИ:
1.одному значению одной переменной величины соответствует множество значений другой,
1. одному значению одной переменной величины соответствует одно значение другой,
2. одному значению одной переменной величины соответствует два значений другой.
8.ОДНОМУ ЗНАЧЕНИЮ ОДНОЙ ПЕРЕМЕННОЙ СООТВЕТСТВУЕТ МНОЖЕСТВО ЗНАЧЕНИЙ ДРУГОЙ, ТО ТАКАЯ ЗАВИСИМОСТЬ ЯВЛЯЕТСЯ:
1.функциональной зависимостью,
2.обратнопропорциональной,
3.корреляционной,
4.прямопропорциональной.
9.ОТКЛОНЕНИЕ ВАРИАНТ ОТ ИХ СРЕДНЕЙ АРИФМЕТИЧЕСКОЙ, ВЫРАЖЕННОЙ В ДОЛЯХ СРЕДНЕКВАДРАТИЧЕСКОГО ОТКЛОНЕНИЯ ЯВЛЯЕТСЯ:
|
|
|
1.коэффициентом корреляции,
2.коэффициентом Стьюдента,
3.стандартным отклонениям,
4.нормированным отклонением,
5.дисперсией.
10.КОЭФФИЦИЕНТ КОРЕЛЯЦИИ УСТАНАВЛИВАЕТ:
1.количественное изменение одной величины от изменения другой,
2.меру тесноты связи между переменными величинами.
3.разность между значением случайной величины и средним арифметическим.
4. нет правильного ответа
11.КОЭФФИЦИЕНТ КОРЕЛЯЦИИ РАНГОВ ПРИМЕНЯЮТ В СЛУЧАЕ, ЕСЛИ ВАРИАНТЫ:
1.отрицательные
2.положительные
3.дробные
4. имеют большую дисперсию
12.МЕТОД РЕГРЕССИИ ПОЗВОЛЯЕТ УСТАНОВИТЬ:
1.зависимость между изменчивостью признаков,
2.меру тесноты связи двух переменных,
3.количественное изменение одной величины по мере изменения другой.
4. нет правильного ответа
13.РЕГРЕССИЯ ВЫРАЖАЕТСЯ:
1.графиком рассеяния,
2.коэффициентом корреляции,
3.уравнением регрессии.
14.ЛИНЕЙНЫЙ КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ ОПРЕДЕЛЯЕТСЯ ПО ФОРМУЛЕ:

15.КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ РАНГОВ ОПРЕДЕЯЕТСЯ ПО ФОРМУЛЕ:

16.УРАВНЕНИЕ ЛИНЕЙНОЙ РЕГРЕССИИ ЭТО:
1. y = ax2+bx+c
2. y = ax+b
3. y = 
4. y = e ax
17.НЕПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ СЛУЖАТ ДЛЯ ПРОВЕРКИ ГИПОТЕЗ О ПАРАМЕТРАХ СОВОКУПНОСТЕЙ:
1.распределяемых по закону Пуассона,
2.имеющих биномиальное распределение,
3.независимо от формы распределения,
4.распределяемых по нормальному закону.
18. t-КРИТЕРИЙ СТЬЮДЕНТА ИСПОЛЬЗУЮТ ДЛЯ:
1.оценки дисперсий,
2.сравнительной оценки средних величин,
3.сравнения частот теоретических и эмпирических.
19. КРИТЕРИЙ ФИШЕРА ИСПОЛЬЗУЮТ ДЛЯ:
1.оценки дисперсий,
2.сравнительной оценки средних,
3.сравнения частот теоретических и эмпирических.
20. НУЛЕВАЯ ГИНОТЕЗА ПРИ ИСПОЛЬЗОВАНИИ КРИТЕРИЯ ФИШЕРА ОТВЕРГАЕТСЯПРИ УСЛОВИИ:
1.Fф=Fст
2. Fф<Fст
3.Fф≥Fст
4.Fф>Fст
21. СУЩНОСТЬ НУЛЕВОЙ ГИПОТЕЗЫ СВОДИТСЯ К ПРЕДПОЛОЖЕНИЮ:
1.разница между генеральными параметрами сравниваемых групп не равна нулю,
2.разница между генеральными параметрами сравниваемых групп равна нулю,
3.различия, наблюдаемых между выборочными характеристиками носят не случайный, а исключительно систематический характер.
22. ПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ СЛУЖАТ ДЛЯ ПРОВЕРКИ ГИПОТЕЗ О ПАРАМЕТРАХ СОВОКУПНОСТЕЙ:
|
|
|
1.распределяемых по закону Пуассона,
2.имеющих биномиальное распределение,
3.распределяемых по любому закону,
4.распределяемых по нормальному закону.
23. t-КРИТЕРИЙ СТЬЮДЕНТА ВЫРАЖАЕТСЯ ФОРМУЛОЙ:
1. 
3. 
4. 
5. 
24. НУЛЕВАЯ ГИПОТЕЗА ПРИ ПРИМЕНЕНИИ t-КРИТЕРИЯ СТЬЮДАНТА ДЛЯСРАВНИТЕЛЬНОЙ ОЦЕНКИ СРЕДНИХ ОТВЕРГАЕТСЯ, ЕСЛИ:
1. tф>tст
2. tф<tст
3. tф≤tст
4. tф=tст
5. tф≥ tст
25. ПРИ ПРИМЕНЕНИНИИ F-КРИТЕРИЯ ФИШЕРА НУЛЕВАЯ ГИПОТЕЗА СОХРАНЯЕТСЯ, ЕСЛИ:
1. Fф>Fст
2. Fф<Fст
3. Fф≥Fст
4. Fф≤Fст
5. Fф= Fст
26. НУЛЕВАЯ ГИПОТЕЗА, Т.Е. ПРЕДПОЛОЖЕНИЕ ОБ ОТСУТСТВИИ РАЗНОСТИ ДВУХ НЕЗАВИСИМЫХ ВЫБОРОК СОХРАНЯЕТСЯ ПРИ ИСПОЛЬЗОВАНИИ КРИТЕРИЯ ВАН-ДЕР-ВАРДЕНА, ЕСЛИ:
1. Xф≥Xст
2. Xф≤Xст
3. Xф=Xст
4. Xф<Xст
5. Xф>Xст
27. F-КРИТЕРИЙ ФИШЕРА ЧИСЛЕННО РАВЕН ОТНОШЕНИЮ:
1.меньшей дисперсии к большей,
2.большей дисперсии к меньшей,
3.равных дисперсии.
4. нет правильного ответа
28. F-КРИТЕРИЙ ФИШЕРА ВЫРАЖАЕТСЯ ФОРМУЛОЙ:
1. 
2. 
3. 
4. 
5. 
29. КРИТЕРИЙ ВАН-ДЕР-ВАРДЕНА ОТНОСИТСЯ К ЧИСЛУ:
1.параметрических критериев,
2.ранговых критериев.
3. непараметрических критериев
4. ранговых и непараметрических критериев
30. КРИТЕРИЙ ВАН-ДЕР-ВАРДЕНА ВЫРАЖАЕТСЯ ФОРМУЛОЙ:
1. 
2. 
3. 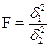
4. 
5. 
31. КРИТЕРИЙ ХИ-КВАДРАТ ПРИМЕНЯЕТСЯ В СЛУЧАЕ, ЕСЛИ ДАННАЯ СОВОКУПНОСТЬ РАСПРЕДЕЛЕНА ПО:
1.нормальному закону,
2.закону Пуассона,
3.биномиальному закону,
4.по любому из перечисленных законов.
32. ПРИ ОЦЕНКЕ ЭМПИРИЧЕСКИХ РАСПРЕДЕЛЕНИЙ ПОДЧИНЯЮЩИХСЯ НОРМАЛЬНОМУ ЗАКОНУ ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ РАВНО:
1.К=N-3
2.К=N-2
3.К=N+3
4.К=N+2
33. НУЛЕВАЯ ГИПОТЕЗА, Т.Е. ПРЕДПОЛОЖЕНИЕ О ПРАВИЛЬНОСТИ ВЫБРАН-
НОГО ЗАКОНА РАСПРЕДЕЛЕНИЯ ДАННОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ С ПОМОЩЬЮ КРИТЕРИЯ ХИ-КВАДРАТ ПОДТВЕРЖДАЕТСЯ, ЕСЛИ:
1.Xф2=Xст2
2.Xф2≥Xст2
3. Xф2<Xст2
4.Xф2>Xст2
5.Xф2≤Xст2
34. КРИТЕРИЙ ХИ-КВАДРАТ ВЫРАЖАЕТСЯ ФОРМУЛОЙ:
1. 
2. 
3. 
4. 
5. 
35. ДЛЯ УСТАНОВЛЕНИЯ ДОСТОВЕРНОСТИ ВЛИЯНИЯ РЕГУЛИРУЕМОГО ФАКТОРА НА РЕЗУЛЬТАТИВНЫЙ ПРИЗНАК В ДИСПЕРСИОННОМ АНАЛИЗЕ ИСПОЛЬЗУЮТ КРИТЕРИИ ФИШЕРА, РАВНЫЙ ОТНОШЕНИЮ:
|
|
|
1.общей дисперсии к дисперсии факториальной,
2.факториальной дисперсии к дисперсии остаточной,
3.дисперсии факториальной к общей дисперсии,
общей дисперсии к дисперсии остаточной.
36. ДИСПЕРСИОННЫЙ АНАЛИЗ ПОЗВОЛЯЕТ УСТАНАВЛИВАТЬ:
1.только достоверность влияния регулируемых и нерегулируемых в опыте факторов на результативный признак,
2.силу влияния регулируемых и нерегулируемых в опыте векторов на результативный признак,
3.достоверность и силу влияния регулируемых и нерегулируемых в опыте факторов на результативный признак.
37. АБСОЛЮТНЫЙ ПРИРОСТ ПОКАЗЫВАЕТ:
1.во сколько раз уровень данного периода больше или меньше базисного,
2.на сколько процентов один уровень больше или меньше базисного,
3.на сколько единиц уровень одного периода больше или меньше предыдущего.
38. КОЭФФИЦИЕНТ РОСТА ПОКАЗЫВАЕТ:
1.во сколько раз уровень данного периода больше или меньше базисного,
2.на сколько процентов один уровень больше или меньше базисного,
3.на сколько единиц уровень одного периода больше или меньше предыдущего.
39. АБСОЛЮТНЫЙ ПРИРОСТ РАСЧИТЫВАЕТСЯ ПО ФОРМУЛЕ:
1.k = 
2.k’=  ·100%
·100%
3.y = at+b
4.∆y = yi-yi-1
5.k’’=k’-100%
40. КОЭФФИЦИЕНТ РОСТА РАСЧИТЫВАЕТСЯ ПО ФОРМУЛЕ:
1.y = at+b
2.k’=  ·100%
·100%
3.∆y = yi-yi-1
4.k’’=k’-100%
5.k = 
41. ТЕМП ПРИРОСТА РАСЧИТЫВАЕТСЯ ПО ФОРМУЛЕ:
1.k’=  ·100%
·100%
2.∆y = yi-yi-1
3.k’’=k’-100%
4.k = 
42. ТЕМП РОСТА РАСЧИТЫВАЕТСЯ ПО ФОРМУЛЕ:
1.k’=  ·100%
·100%
2.∆y = yi-yi-1
3.k’’=k’-100%
4.k = 
43. ОТНОСИТЕЛЬНЫЙ ПОКАЗАТЕЛЬ, ПОКАЗЫВАЮЩИЙ НА СКОЛЬКО ПРОЦЕНТОВ ОДИН УРОВЕНЬ БОЛЬШЕ ИЛИ МЕНЬШЕ БАЗИСНОГО ЭТО:
1.абсолютный прирост,
2.коэффициент роста,
3.темп прироста,
4.темп роста.
44. МЕТОД УДЛИНЕНИЯ ПЕРИОДОВ ЗАКЛЮЧАЕТСЯ В:
1.построение графика зависимости данной исследуемой величины от времени,
2.вычисление средней величины объединенных периодов, которые затем наносят на график,
3.вычисление значений по формуле y = at+b,
4.вычисление последовательной серии сплетающихся средних, которые затем наносятся на график.
45. ПРОЦЕСС РАСЧЕТА ТЕОРЕТИЧЕСКИ ОЖИДАЕМЫХ ВЕЛИЧИН НОСИТ НАЗВАНИЕ:
1.сравнивание динамических рядов,
2.выравнивание временных рядов,
3.удлинение временных рядов,
4.корреляция временных рядов.
46. О ДОСТОВЕРНОСТИ ВЛИЯНИЯ ДАННОГО ФАКТОРА В ДИСПЕРСИОННОМ АНАЛИЗЕ НА ИЗМЕНЧИВОСТЬ ПРОИЗНАКА СУДЯТ:
1.по критерию Стьюдента,
2.по критерию Фишера,
3.по критерию хи-квадрат,
4.по критерию Ван-дер-Вандера.
РАЗДЕЛ 2
|
|
|


