 |
Изотермические реакторы периодического действия с постоянным объемом
|
|
|
|
Для реакторов идеального смешения период-го действия пост- объема основной з-н кинетики:
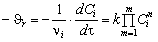
Для того, чтобы установ конкретный вид этого ур-я, кот будет описывать ход изуч-го хим процесса, и опред константы этого ур-я (К, Еа и порядок р-и), необх прибегнуть к экспер-му опред-ю Сi = f (τ) или хi = f (τ) и послед-му анализу.
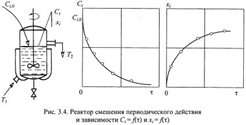
Известны 2 метода анализа экспер-х кинетич кривых: интегральный и дифференциальный.
1. Предлагают мех-м р-и и записывают соотв-е выр-я скорости:
. (3.23)
В уравнении (3.23) делят переменные.
. (3.24)
Интегрируя ур-е (3.24), получают
. (3.25)
Если интеграл левой части уря (3.25) трудно найти аналитически, то м исп-ть граф метод-опред площади под кривой от 1/Сп от Сi (рис. 3.5, а)
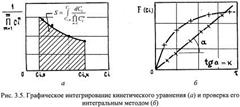
2. По экспер-м знач-м конц-ции компонентов опред-ют численное значение F (Ci) для различ моментов вр. Строят график зав-ти F (Ci) = f (τ). Если он явл прямой линией (рис. 3.5, б), то принятое ур-е согласуется с экспе-ми данными; если экспер-е точки не ложатся на прямую линию, необх испытать др- ур-я, пока не будет удовл соответ-е.
Интегр- метод удобен для анализа простых в кинетическом отношении х т. Рассмотрим несколько примеров.
Пример 1. Пусть в системе протекает реакция
А→Продукты.
Предположим, что по механизму эта реакция относится к реакциям первого порядка. Тогда
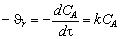. (3.26)
Разделяя переменные и интегрируя, получим
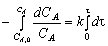(3.27)
или
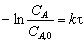. (3.28)
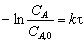. (3.28)
В химической технологии кинетическое уравнение, как было сказано ранее, обычно выражают через степень превращения. Так для периодических реакторов с постоянным объемом можно записать, что СА = СА ,0(1 – хА). Тогда уравнение (3.26) принимает вид:
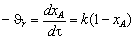(3.29)
Интегрируя это уравнение, получим
, (3.31)
т. е. результат, эквивалентный уравнению (3.28).
|
|
|
График зависимости –ln(1 – xA) или –ln CA / CA ,0 от τ для уравнений этого типа есть прямая линия, выходящая из начала координат (рис. 3.6, а).
Пример 2. Допустим, что в системе протекает реакция
А+В→ Продукты,
которая по механизму относится к реакциям второго порядка
. (3.32)
Заметив, что количества А и В, прореагировавшие за время τ, равны СА ,0 ХА = СВ ,0 ХВ, и для А, и для В можно написать уравнение (3.33), используя в качестве переменной ХА:
Обозначив через М = СВ ,0/ СА ,0 начальное соотношение реагентов, получим
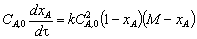. (3.34)
После разделения переменных находим:
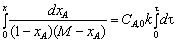. (3.35)
Раскладывая далее подынтегральную функцию на простые дроби, проводя интегрирование и необходимые преобразования, получим окончательный результат:
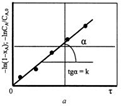
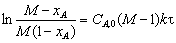, M ≠1. (3.36)
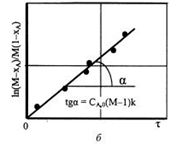
Из рис. 3.6, б следует, что для реакции второго порядка график зависимости ln(M – XA)/ M (1 – XA) от τ является прямой линией с тангенсом угла наклона СА ,0(М –1) k.
Замечание 1. Если СВ ,0 >> СА ,0, то СB почти не меняется и уравнение (3.32) приближается к уравнению (3.26) для реакций первого порядка
. (3.37)
В этом уравнении k набл = kCB – наблюдаемая константа скорости процесса. Таким образом, реакция второго порядка становится реакцией псевдопервого порядка.
Замечание 2. В особом случае, когда реагенты подаются в реактор с одинаковыми концентрациями, интегральное уравнение скорости (3.36) становится неопределенным и для его решения требуется выполнить предельный переход. Можно избежать этого затруднения, если вернуться к первоначальной форме кинетического уравнения и решить его для этого частного случая.
Так, для реакции второго порядка при одинаковых начальных концентрациях реагентов А и В или для реакции 2А → Продукты
дифференциальная форма кинетического уравнения принимает вид
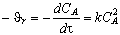(3.38)
или
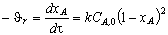. (3.39)
После интегрирования уравнений (3.38) и (3.39) получаем
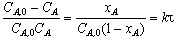. (3.40)
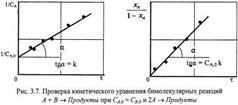
Таким образом, график зависимости 1/ CA от τ или ХА /(1 – XA) от τ представляет собой прямую линию (рис. 3.7).
|
|
|
Пример 3. Рассмотрим случай, когда вещество А разлагается или исчезает по двум различным направлениям, которые являются элементарными реакциями
Скорости исчезновения и образования компонентов реакции будут определяться уравнениями 
;
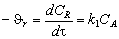; (3.42)
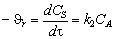. (3.43)
В таких реакциях, измеряя только какую-либо одну концентрацию СА, СR или СS, нельзя найти k 1 и k 2. Значения k 1 и k 2 можно найти, используя все три дифференциальные уравнения скорости.
. Значения k 1 и k 2 можно найти, используя все три дифференциальные уравнения скорости.
Уравнение (3.41) имеет первый порядок и может проинтегрироваться, что приводит к равенству
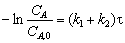. (3.44)
Если построить график этого у-я так, как на рис. 3.8, то тангенс угла наклона будет = k 1 + k 2. Разделив затем ур-е (3.42) на (3.43), получим
(3.45)
или после интегрирования находим, что
. (3.46)
Этот результат показан также на рис. 3.8. Таким образом, наклон прямой в координатах СR – CS дает отношение k 1/ k 2. Зная k 1/ k 2, а также k 1 + k 2, можно найти k 1 и k 2.
|
|
|
