 |
Текущая стоимость аннуитета
|
|
|
|
Основой всех расчетов, проводимых при обосновании и анализе инвестиционных проектов, является сопоставление затрат, которые необходимо осуществить в настоящее время, и тех денежных поступлений которые можно получить в будущем.
В решении этой проблемы помогает подход, предполагающий определение текущей (современной) стоимости аннуитета. На этой основе достаточно четко можно представить, насколько окупится сегодняшнее вложение средств завтрашними выгодами.
Понять смысл такого анализа будет легче, если мы рассмотрим в качестве примера инвестиционный проект, предполагающий получение 1 млн. руб. в конце каждого из 5 последующих лет. Приведенную стоимость (исходя из процентной ставки – нормы дисконта – на уровне 10 % годовых) для каждого из будущих притоков денег мы можем определить с помощью формулы (5.2) и приложения 3. Полученные результаты приведены в табл. 5.2.
Таблица 5.2
Расчет текущей стоимости аннуитета
| Годы | Денежные потоки (денежные поступления), млн. руб. | Текущая стоимость будущих денежных поступлений, млн. руб. |
1,00  =0,909 =0,909
| ||
1,00 
| ||
1,00 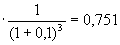
| ||
1,00  0,683 0,683
| ||
1,00 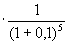 =0,621 =0,621
| ||
| Итого текущая стоимость 3,79 |
Графически тот же процесс изображен на рис. 5.2.

Рис. 5.2. Схема формирования текущей стоимости аннуитета
Логика такого пересчета будет неизменной для любого числа лет жизни объекта, созданного в результате инвестиций. Расчет был проведен по формуле (5.2) следующим образом:
 = j.
= j.
Отсюда общее уравнение расчета текущей стоимости аннуитета:
 =
=  , (5.5)
, (5.5)
где PMTt – будущие поступления денежных средств в конце периода t;
E – норма доходности по инвестициям;
K – число периодов, на протяжении которых в будущем поступят доходы от современных инвестиций.
|
|
|
В случае, если денежные поступления одинаковы в каждом периоде, формулу можно упростить и представить в следующем виде:
 =
=  , (5.6)
, (5.6)
где  - текущая (современная) стоимость аннуитета стоимостью в 1руб. в конце каждого из k периодов при ставке доходности на уровне E.
- текущая (современная) стоимость аннуитета стоимостью в 1руб. в конце каждого из k периодов при ставке доходности на уровне E.
Найти нужное значение с помощью формул (5.5) и (5.6) можно благодаря системам электронных таблиц или справочным таблицам (приложение 4). Если для решения этой задачи мы воспользовались справочной таблицей, содержащей значения аннуитета в 1 руб., то, по сути дела, нашли коэффициент приведения будущей стоимости к современной (коэффициент дисконтирования), и далее надо просто умножить этот коэффициент на реальные суммы аннуитета.
Пример 5.3. Предположим, что для приобретения нового оборудования необходимы денежные средства в сумме 100 тыс. руб., которые обеспечат ежегодное получение денежных поступлений после уплаты налогов в сумме 25 тыс. руб. в течение 6 лет без существенных ежегодных колебаний. Хотя оборудование после 6 лет эксплуатации не будет полностью изношено, тем не менее, вряд ли возможно предполагать, что на этот момент времени его стоимость будет превышать стоимость лома. Затраты на ликвидацию будут возмещены за счет выручки от продажи лома. Линейная амортизация за эти 6 лет (16 667 руб. за год) будет соответственно включена в сумму денежных поступлений 25 тыс. руб.
Чтобы оценить этот проект в самом первом приближении, достаточно прикинуть, покроет ли текущая (современная) стоимость будущих денежных поступлений те затраты, которые фирме придется осуществить сейчас. Реально это означает, что нам следует определить чистую текущую стоимость, которую фирма получит от реализации такого проекта.
При проведении расчетов будем исходить из ставки доходности (нормы дисконта) на уровне 10% годовых.
Результаты расчетов сведены в табл. 5.3.
|
|
|
Как показали расчеты, для данного проекта чистая текущая стоимость оказалась положительной. Иными словами, осуществление инвестиционного проекта привело к росту капитала фирмы на 8 850 руб. в современном исчислении. Следовательно, инвестиции оказались полезными и привели к росту ценности фирмы.
| Период времени (годы) | Инвестиции (руб.) | Денежные поступления | Текущая стоимость 1 руб. денежных потоков разных лет (коэффициенты дисконтирования при ставке 10%) | Текущая стоимость денежных потоков разных лет, руб. |
| 0 (сегодня) | 100 000 | 1 000 | -1 000 | |
| 25 000 | 0,909 | +22 725 | ||
| 25 000 | 0,826 | +20 650 | ||
| 25 000 | 0,751 | +18 775 | ||
| 25 000 | 0,683 | +17 075 | ||
| 25 000 | 0,621 | +15 525 | ||
| 25 000 | 0,564 | +14 100 | ||
| Чистая текущая стоимость проекта | +8 850 |
Таблица 5.3
Расчет текущей стоимости денежных потоков
5.
Ценность ренты
При оценке инвестиционных проектов, когда решается вопрос о предельно допустимой сумме вложений, полезно рассмотреть проблему с точки зрения альтернативного дохода, обеспечиваемого вложениями рентного типа.
Классическим примером такого рода альтернативного вложения средств является банковский бессрочный текущий (сберегательный) счет, процентный доход по которому полностью изымается сразу после его начисления. Такой вид инвестиций для противопоставления аннуитету называют перпетуитетом (perpetuity – вечность). В этом случае реально возникает ситуация, когда основная сумма вклада как бы «зарабатывает» деньги на предстоящий год, а срок жизни инвестиций неограничен. В этом случае годовой доход определяется по формуле
PMT = PV · E, (5.7)
где PV – основная сумма сбережений на банковском счете;
E – процентная ставка дохода, выплачиваемая банком по счетам данного типа.
Отсюда мы можем прийти к пониманию ценности инвестиций, обеспечивающих аналогичный приток денежных средств. Для этого формулу (5.7) представим в виде
 . (5.8)
. (5.8)
Использование этой формулы подводит нас к пониманию простой логики инвестиционного анализа. Ее суть хорошо рассматривается на простейшем примере. Предположим, что у нас есть счет в банке на 1 млн. руб. (PV) под 12% годовых. Это означает, что в начале января каждого года мы можем снять с этого счета начисленные проценты в сумме 120 тыс. руб. (PMT). Исходя из этого, с помощью формулы (5.8) мы можем теперь найти ту предельную величину инвестиций, которую (при ставке доходности 12% годовых) стоит вложить ради получения такого дохода. Она будет равна 120 000/0,12 = 1 000 000 руб.
|
|
|
|
|
|


