Силовой расчёт группы Ассура

Рассмотрим группу Ассура второго класса второго вида, состоящую из шатуна 2 и ползуна 3 (рис. 5.4,а) и входящую в состав, например, кривошипно-ползунного механизма, одного из самых простых четырёхзвенных механизмов.

Группа изображается в масштабе . На ползун 3 действует внешняя сила и сила инерции ползуна , на шатун действуют сила инерции , приложенная в точке S₂, и момент сил инерции . Крайними кинематическими парами группы Ассура являются вращательная пара в точке А и поступательная пара ползуна 3 со стойкой. Отбрасывая кривошип 1 и стойку 0, освобождаем группу Ассура от связей и вместо них прикладываем неизвестные реакции в точке А и в поступательной паре, проведя её линию действия через точку В перпендикулярно направляющей. Отброшенные звенья показаны на схеме штриховыми линиями.

Записываем уравнение равновесия всей группы в целом в векторной форме:

.

В правой части этого уравнения стоит нуль, указывающий на равновесие. В этом уравнении первый вектор известен по величине и по направлению, второй известен по направлению, третий известен по величине и по направлению, четвёртый неизвестен совсем. Уравнение в таком виде не может быть решено, так как в нём три неизвестных параметра, а необходимо только два. Для сокращения количества неизвестных разложим вектор на составляющие, одну из которых, , направим перпендикулярно шатуну 2 и назовём тангенциальной составляющей. Вторую, , направим вдоль шатуна и назовём нормальной составляющей. Данная операция соответствует равенству . Составляющая определяется из уравнения равновесия шатуна 2 в форме моментов сил относительно точки В:

,

из которого имеем 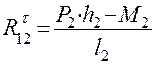. Размеры плеч в этих выражениях измеряются в миллиметрах () на схеме механизма и с помощью масштаба переводятся в натуральную величину. Причём плечо есть кратчайшее расстояние линии действия силы от точки B.

Если результат расчёта по приведённому выражению оказывается отрицательным, то в дальнейшем направление следует принять обратным по отношению к принятому на схеме. Составляющая и реакция определяются путём построения векторного многоугольника сил (рис. 5.4,б). Для определения реакции во вращательной паре В между шатуном и ползуном необходимо построить на основе уравнения равновесия план сил шатуна 2 отдельно от ползуна 3 (или ползуна 3 отдельно от шатуна 2). Например, уравнение равновесия шатуна 2 запишется так:

.

В этом уравнении первые два вектора известны полностью, третий вектор определится построением треугольника сил.

Силовой расчёт кривошипа

Как и в случае группы Ассура, необходимо прежде составить расчётную схему, приложив известные силы (рис. 5.5,а). В точке А прикладывается реакция со стороны отброшенного шатуна , которая равна и противоположна найденной выше реакции . В центре масс кривошипа прикладывается сила инерции, равная по величине и направленная к точке А (это соответствует постоянству угловой скорости кривошипа).

В точке О кривошипа действует реакция со стороны стойки, которую необходимо определить. Кроме того, к кривошипу необходимо приложить так называемый уравновешивающий момент , действующий на него со стороны машины-двигателя, приводящей в движение данную машину. Вместо уравновешивающего момента можно приложить уравновешивающую силу , задав точку её приложения, а направление выбрав произвольным. Выбор между уравновешивающими моментом и силой зависит от способа передачи движения от двигателя к технологической машине. Если этот способ в задаче не оговорен, то расчётчик (студент) делает выбор по своему усмотрению. Остановимся здесь на выборе уравновешивающего момента. Определим величину этого момента, составив уравнение равновесия кривошипа в форме моментов сил относительно точки О: , из которого ясно, что . Для нахождения реакции строится план сил согласно приведённому выше уравнению (рис. 5.5,б). Если приложить к кривошипу вместо уравновешивающего момента уравновешивающую силу, то она войдёт в векторное уравнение равновесия и повлияет на реакцию .