 |
Эвольвента окружности, её свойства и уравнение
|
|
|
|
Эвольвента – это траектория точки прямой линии (производящей прямой), перекатывающейся без скольжения по окружности.
Образование эвольвенты можно представить как траекторию, описываемую остриём карандаша, привязанного к концу нити, сматываемой с катушки, установленной своей осью перпендикулярно плоскости листа бумаги.
Свойства эвольвенты
1) Нормаль к эвольвенте является касательной к основной окружности.
2) Центры кривизны эвольвенты лежат на основной окружности, так что основная окружность представляет собой эволюту, т. е. геометрическое место центров кривизны эвольвенты.
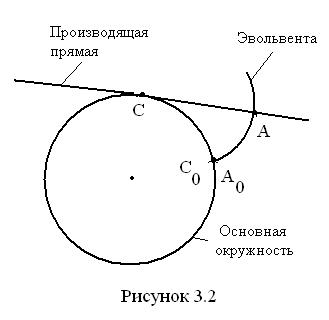3) Радиус кривизны эвольвенты в данной точке равен отрезку производящей прямой, заключённому между данной точкой эвольвенты и точкой касания производящей прямой с основной окружностью, ρА = AC. В точке начала эвольвенты её радиус кривизны равен нулю, ρA0 = 0.
4) Радиус кривизны эвольвенты в данной точке равен дуге основной окружности, заключённой между точкой начала эвольвенты и точкой касания этой прямой с основной окружностью, ρA = 
C0C.
5) Правая и левая ветви эвольвенты симметричны.
6) Все точки эвольвенты лежат снаружи от основной окружности.
Уравнение эвольвенты
Для получения уравнения эвольвенты обратимся к рис. 3.3. Положение произвольной точки Ay эвольвенты в полярной системе координат определяется двумя координатами относительно её начального радиус-вектора OA0 (или OC0): 
длиной радиус-вектора R y и углом θy. Радиус-вектор Ry определим из прямоугольного треугольника OAyCy:
Для определения полярного угла θ y сначала выразим длину дуги основной окружности через её радиус и центральный угол:
Выразим теперь противолежащий углу αy катет AyCy в ∆OAyCy:
|
|
|
На основании четвёртого свойства эвольвенты имеем
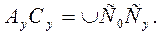
Подставляя в это равенство соответствующие выражения и решая его относительно θ y, получаем
.
В этих математических выражениях и на рис. 3.3 угол αy называется профильным углом эвольвенты. Разность между тангенсом какого-либо угла и самим углом называется эвольвентной функцией и обозначается тремя первыми буквами латинского названия эвольвенты involute, т. е. inv, так что окончательно уравнение имеет вид:
θy = invαy.
В математических справочниках приводятся таблицы эвольвентной функции, в которых аргумент αy изменяется от нуля до нескольких десятков градусов.
Элементы зубчатого колеса
Здесь рассматриваются те элементы колеса, которые относятся к его ободу, где располагаются зубья (рис. 3.4).
Шаг колеса p – это расстояние по делительной окружности между одноимёнными профилями двух соседних зубьев, p = π·m. Шаг включает два параметра – толщину зуба s и ширину впадины e. Если s = e, то имеем колесо с равноделённым шагом, в противном случае имеем колесо с неравноделённым шагом.
Делительная окружность (её радиус 
, в зацеплении двух колёс имеет индекс номера колеса):
– делит зуб на головку и ножку;
– модуль m на этой окружности имеет стандартное значение;
– радиус окружности имеет величину r = 0,5m 
;
– в точке на делительной окружности профильный угол эвольвенты αy = 20º и обозначается буквой α без индекса.
Основная окружность является базовой для образования эвольвенты (от неё начинается эвольвентная часть зуба). Радиус этой окружности получается из рассмотрения прямоугольного треугольника с углом при вершине O, равным α, и одним из катетов, равным b, и гипотенузой, равной : b = ·cos α.
Окружность вершин является габаритной окружностью колеса, её радиус определяется формулой
,
где 
– высота головки зуба, причём 
. Множитель перед модулем называется коэффициентом высоты головки зуба и равен по величине 1, т. е. 
.
|
|
|
Диаметр окружности вершин является диаметром заготовки для изготовления зубчатого колеса.
Окружность впадин ограничивает зуб у основания, её радиус равен
,
где 
– высота ножки зуба, определяемая равенством 
, второе слагаемое в скобках называется коэффициентом радиального зазора и имеет величину 
.
Контур зуба от основной окружности до окружности вершин очерчен эвольвентой, которая сопрягается с окружностью впадин переходной кривой (эквидистантой удлинённой эвольвенты).
|
|
|
