Чистовая и финишная обработка беговых дорожек конических (роликовых) подшипников качения

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ФОРМООБРАЗОВАНИЯ

ПОВЕРХНОСТЕЙ

2.1. Основы формообразования поверхностей деталей

Поверхность любой детали является комплексной, состоящей из элементарных поверхностей, которые в изделии могут быть сопрягаемыми, присоединяемыми, зацепляемыми, базовыми, свободными, открытыми и др.

Детали могут быть конструктивно простыми, но в зависимости от их габаритов, массы, состояния производства могут оказаться технологически сложными. Например, поверхность детали типа «тело вращения» имеет криволинейную образующую. К таким деталям относятся сферические, параболоидные, торообразные и т. п. Они конструктивно просты, технологически просты при изготовлении на оборудовании с ЧПУ, но в случае изготовления их на универсальном оборудовании без систем ЧПУ требуется проводить специальную технологическую подготовку, изготовлять технологическую оснастку: установочно-зажимные, контрольные приспособления, специальный режущий инструмент. В результате резко возрастает трудоемкость изготовления деталей и себестоимость производства.

Особенно сложно решаются вопросы формообразования: зубчатых поверхностей дисковыми, реечными и червячными инструментами, поверхностей режущих инструментов - фасонных дисковых и концевых фрез, абразивных кругов и червяков, резцов для строгания винтовых поверхностей, зуборезных гребенок, червячных фрезы, долбяков, шеверов, винтовых сверл и т. д.

В этой и последующих лекциях кратко рассмотрены теория и метод решения вопросов формообразования поверхностей деталей и поверхностей режущей части инструментов. Метод является единым для дисковых, реечных и червячных инструментов: он является общим для наружных и внутренних поверхностей любого профиля при любом положении инструмента относительно обрабатываемой детали, при обработке поверхностей по способу фасонной обработки (копирования) и по способу огибания (безцентроидного и центроидного – обкатки), при обработке единичной поверхности детали и при обработке зубчатой поверхности; метод является аналитическим и позволяет определять:

а) координаты профиля производящей поверхности инструмента по заданным параметрам поверхности детали и параметрам установки инструмента (прямая задача);

б) координаты профиля обработанной поверхности детали по заданным параметрам производящей поверхности и параметрам установки инструмента (обратная задача);

в) координаты переходных кривых и подрезов на профиле обработанной поверхности; границы и вид этих искажений профиля детали;

г) оптимальные параметры установки инструмента для получения наилучшего профиля инструмента с технологической и эксплуатационной точек зрения, а также для получения поверхности детали без переходных кривых и подрезов;

д) форму передних и задних поверхностей режущей части инструментов;

е) погрешности, вызванные заменой геометрически точной поверхности режущей части инструмента технологически удобными поверхностями;

ж) влияние допусков изготовления и установки инструментов на точность обработки поверхностей деталей;

3) отклонения профиля поверхностей, деталей, возникающих в результате переточек и правок инструментов;

и) профили резцов и шлифовальных кругов для затылования и заточки зубьев инструментов.

Метод предусматривает решение вопросов формообразования поверхностей деталей и формообразования поверхностей режущей части инструментов вплоть до расчета профиля и установки инструментов второго порядка. Это необходимо при проведении технологической подготовки производства, включая нормирование работ и расчет технологической себестоимости не только в производстве, но и для всего предпроизводственного периода.

Все аналитические расчеты и экспериментальные работы должны заканчиваться программой для реализации на ЭВМ соответствующего алгоритма, который представляет своеобразный механизм, связывающий через параметры установки инструмента параметры обрабатываемой детали с параметрами инструмента. С помощью такой программы можно решать не только однозначную задачу, но и широко производить анализ влияния каждого параметра инструмента на условия формообразования поверхностей для определения его оптимальных значений.

Исходным моментом при этом является знание технологических возможностей оборудования, имеющегося у производителя, или которое он в состоянии приобрести.

2.2 Движения инструмента относительно детали

Теоретическую форму обработанной поверхности детали без микронеровностей и других отклонений будем называть номинальной. Номинальная поверхность детали может быть определена двумя параметрами; например, криволинейные координатами и (рис. 2.1, а) и тогда в системе координат , связанной с деталью, уравнение номинальной поверхности в параметрическом виде будет

), (2.1)

где 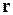-радиус-вектор, имеющий начало в точке О начала системы координат .

Будем считать, что нормаль к номинальной поверхности детали в данной ее точке А будет всегда обращена в сторону от материала детали. Тогда радиус кривизны кривой EF сечения номинальной поверхности любой плоскостью Q будет положительным, если вогнутость кривой EF обращена в сторону нормали к кривой EF (рис. 2.1,6).

а	б	в
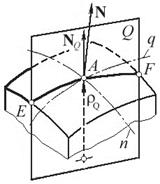
Рис. 2.1 Криволинейные координаты на номинальной поверхности детали

Криволинейные координаты на поверхности могут быть выбраны в широких пределах. Удобнее выбирать их в зависимости от способа образования номинальной поверхности инструментом. При обработке поверхности детали инструмент выполняет две функции: формообразования поверхности и срезания припуска. Обе функции инструмент осуществляет режущими кромками, совершая комплекс движений относительно детали. Режущая кромка инструмента геометрически представляет собой отрезок линии. На инструменте может быть одна режущая кромка или множество. Во втором случае режущие кромки располагается на поверхности, которую называют производящей (рис. 2.2). Таким образом, с геометрической точки зрения формообразование номинальной поверхности детали осуществляется или линией или поверхностью.

а	б	в
Рис. 2.2 – Производящие поверхности инструментов: а – цилиндрическая; б – тело вращения; в – винтовая; е и f – координатные линии

а	б
Рис. 2.3. Режущие кромки инструментов

Режущая кромка инструмента как линия определяется одним параметром . Уравнение режущей кромки в системе координат инструмента (рис. 2.3, а) может быть представлено в виде

(2.2)

Производящая поверхность инструмента определяется двумя параметрами - криволинейными координатами е и f (рис. 2.3, б). Уравнение производящей поверхности в системе координат инструмента может быть представлено в виде

(2.3)

Режущая кромка инструмента является жесткой линией, а производящая поверхность - жесткой поверхностью, т. е. во время работы инструмента они не меняет своей формы.

Режущий инструмент обрабатывает поверхность детали контактным способом, поэтому его движения для выполнения функции формообразования должны быть такими, чтобы производящая поверхность или режущая кромка, перемещаясь относительно детали, имели с ее номинальной поверхностью касание. С другой стороны, для выполнения функции срезания припуска движения инструмента должны быть такими, благодаря которым припуск на номинальной поверхности детали можно было разделить режущими кромками на отдельные слои, срезаемые по требуемому закону.

Положение инструмента относительно детали определяется положением системы координат инструмента относительно системы координат хуz детали. Это положение оно характеризуется шестью величинами: расстояниями , , параллельного переноса начала системы координат вдоль осей х, у, z и углами , , поворота системы координат хуz относительно осей , , .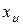

Закон движения инструмента относительно детали определяется видом зависимостей величин , , , , , от параметра движения. Если параметром движения является одно из перечисленных движений, например - ое, то при движении инструмента его линейные и угловые перемещения по координатам описываются зависимостями

2.4

Инструмент в процессе обработки детали совершает несколько движений и каждое из них имеет свое назначение.

а	б	в
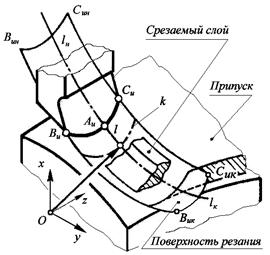
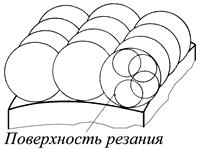
Рис. 2.4. Образование замкнутой поверхности резания: а – режущей кромкой при точении или фрезеровании; б – при торцовом точении; в – производящей поверхностью при шлифовании с радиальной подачей

а	б
Рис. 2.5 – Образование разомкнутой поверхности резания

Срезание припуска с номинальной поверхности детали осуществляется слоями. Движение инструмента, при котором его одна режущая кромка срезает один слой, называют движением резания или главным движением. Это движение инструмент осуществляет при изменении некоторого параметра в пределах от его начального значения до конечного . Совершая движения резания, режущая кромка инструмента описывает поверхность резания, уравнение которой в системе координат (рис. 2.4, 2.5) будет , где и — криволинейные координаты на поверхности. резания, причем - параметр формы режущей кромки.

Поверхность резания может быть замкнутой (см. рис. 2.4) и разомкнутой (см. рис 2.5).

При замкнутой поверхности резания режущая кромка инструмента, совершая движение резания при изменении параметра от до , придет в свое начальное положение. Это характерно для точения фасонным резцом и прорезания канавок. Замкнутая поверхность резания образуется и при шлифовании с радиальной подачей поверхностей вращения фасонно-заправленным кругом.

При разомкнутой поверхности резания после осуществления движения резания инструмент для возвращения режущей кромки из конечного положения в исходное положение должен совершить обратное, холостое движение, которое может быть осуществлено при изменении параметра от до . Такая поверхность резания образуется при точении с продольной или радиальной подачей, нарезании резьбы, долблении

На рис. 2.5, б показана обработка зубчатого венца на зубодолбежном станке с ЧПУ фирмы Лоренц (ФРГ), совмещенная с точением базовой поверхности ступицы.

Для срезания всего припуска инструмент должен совершить серию движений резания, благодаря которым его режущая кромка создает семейство поверхностей резания, где каждая последующая поверхность резания смещена относительно предыдущей (рис. 2.6). Движение инструмента, вызывающее такое смещение поверхностей резания, называется подачей, поэтому параметр подачи является параметром семейства поверхностей резания. Если инструмент образует номинальную поверхность производящей поверхностью, то его режущие кромки, находящиеся на последней и смещенные друг относительно друга по некоторому закону, опишут семейство поверхностей резания за одно движение резания. В этом случае подача как движение заменяется таким расположением на теле инструмента множества режущих кромок, при котором за одно движение резания многолезвийный инструмент осуществит ту же схему срезания припуска, что и однолезвийный инструмент за множество движений резания. К процессам, в которых кинематическая подача заменяется конструктивной подачей, относятся: протягивание – плоское, контурное, круговое; нарезание резьбы метчиком, плашкой, резьбонарезной головкой.

Рис. 2.6 – Семейство поверхностей резания

Инструмент может иметь несколько подач. Каждая подача вызывает образование семейства поверхностей. При большом числе подач режущая

а
б
в
г	д
Рис. 2.7 – Система семейств поверхностей резания, образуемая режущей кромкой инструмента

кромка инструмента может создать очень сложную систему семейств поверхностей резания. При любой такой системе для срезания припуска имеют значение все подачи, а для формообразования только те из них, которые будут осуществляться в период касания поверхности резания с номинальной поверхностью детали. Закон, по которому создана система одного или нескольких семейств поверхностей резания, определяет схема срезания припуска и схема формообразования.

Сложность схемы формообразования определяется количеством подач инструмента. Номинальная поверхность детали может совпадать с поверхностью резания (при формообразовании подача инструмента отсутствует) (рис. 2.7, а); быть огибающей поверхностью однопараметрического семейства поверхностей резания (при формообразовании инструмент имеет одну подачу) (рис. 2.7, б); быть огибающей поверхностью двухпараметрического семейства поверхностей резания (при формообразовании инструмент имеет две подачи) (рис. 2.7, в); быть огибающей поверхностью системы семейств поверхностей резания, построенных при наличии трех параметров семейств, трех подач (рис. 2.7, г); при наличии четырех параметров семейств, четырех подач (рис. 2.7, б) и т. д.

Таким образом, для срезания припуска и формообразования номинальной поверхности детали инструмент должен совершать движения резания и подачи. Однако при обработке детали кроме этих движений инструмент осуществляет дополнительно несколько так называемых транспортных движений: подход к детали и отход от нее; холостые, обратные движения; переход от одной элементарной поверхности к другой (например, при делении на зуб в случае обработки зубчатой детали); переход от одной детали к другой (при последовательной обработке партии или потока деталей) и др. Эти движения не влияют на условия срезания припуска и формообразование детали, но влияют на операционное время.

Движения резания и подачи могут осуществляться инструментом последовательно или одновременно. Принято называть простым движение резания, если оно осуществляется при изменении только одного параметра , и сложным, если это движение осуществляется при одновременном изменении параметра и одного или нескольких параметров подач. Простое движение осуществляется при строгании плоской поверхности на строгальном или долбежном станке. При этом совершается возвратно-поступательное движение, включающее рабочий ход - период резания и вспомогательный ход – отвод резца в исходное положение. Сложное движение осуществляется при протягивании, когда за один рабочий ход образуется количество поверхностей резания, равное количеству режущих зубьев. Подачей в этом случае является подъем на зуб.

Формы поверхностей резания при простом или сложном движениях резания будут несколько отличаться друг от друга и в соответствии с этим будут отличаться размеры срезаемых слоев, однако это отличие практически незначительно и поэтому при расчете схемы резания им можно пренебречь.

Для формообразования номинальной поверхности детали безразлично, какое движение резания совершает инструмент - простое или сложное. Поэтому при решении вопросов формообразования поверхностей деталей удобнее считать, что инструмент совершает только простые движения резания.

2.3 Схемы формообразования поверхностей инструментами

Функции инструмента - срезания припуска и формообразования обычно находятся в противоречии. Рациональная схема формообразования детали инструментом часто не соответствует рациональной схеме срезания припуска и наоборот. При проектировании режущего инструмента конструктор должен стремиться к тому, чтобы противоречие между этими схемами было решено оптимально. Условия для такого решения теоретически имеются и заключаются в следующем: а) хотя движения инструмента, необходимые для формообразования номинальной поверхности детали и, соответственно, для срезания припуска, тесно связаны с формой номинальной поверхности детали, в общем случае их связь неоднозначна, поэтому в зависимости от принятой схемы формообразования детали имеется большая или меньшая свобода выбора некоторых из них; б) режущая кромка инструмента в общем случае состоит из двух участков: формообразующего, точки которого в процессе работы инструмента приходят в соприкосновение с номинальной поверхностью детали, и неформообразующего. Форма последнего не связана с формой номинальной поверхности детали и может быть выбрана в зависимости от рационального резания. Кроме этого в конструкцию инструмента могут быть внесены режущие кромки, которые не имеют формообразующих участков (черновые режущие кромки) и поэтому их форма и расположение могут быть полностью выбраны только из условий получения желаемого закона срезания припуска. Если режущие кромки инструмента имеют только формообразующие участки, то схема срезания припуска является одновременно и схемой формообразования номинальной поверхности детали, так как в резании будут участвовать те же точки режущих кромок, что и при формообразовании.

Если режущие кромки инструмента кроме формообразующих имеет неформообразующие участки и, особенно, если инструмент содержит черновые, сплошь неформообразующие режущие кромки, то схема резания не совпадает со схемой формообразования и в результате соответствующего расположения режущих кромок на корпусе инструмента можно (в некоторой степени) при рациональной схеме формообразования можно биться и приемлемой схемы срезания припуска.

Для успешного решения указанного противоречия между функциями инструмента большое значение имеет схема формообразования номинальной поверхности детали, а именно: какие возможности имеет она в смысле свободы выбора формы режущей кромки, формы производящей поверхности и законов движений инструмента. Определим эти возможности схем формообразования.

Пусть номинальная поверхность детали является огибающей однопараметрического семейства поверхностей резания (см. рис. 2.7, б). Ее уравнение в системе координат , связанной с деталью, имеет вид

, (2.6)

где - параметр семейства, т. е. параметр подачи.

Номинальная поверхность задана уравнением (2.1), выберем на этой поверхности криволинейные координаты и таким образом, чтобы движение инструмента вдоль координатных линий осуществлялось при изменении параметра движения резания, а движение его вдоль координатных линий - при изменении параметра подачи .

Приравнивая уравнения (2.1) и (2.6), получим

. (2.7)

Из этого уравнения видно, что три параметра инструмента- k, l, s находятся в зависимости от двух координат номинальной поверхности детали и . Поэтому при проектировании инструмента вид, зависимости от и одного из параметров инструмента можно выбирать, а вид зависимостей остальных двух - рассчитать по уравнению (2.7). Например, выберем вид зависимости 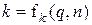и подставим это значение в уравнение (2.7). Получим

(2.8)

Учитывая условия выбора криволинейных координат и на номинальной поверхности детали, можно заключить, что при фиксированном значении параметр фиксируется и значение координаты . При фиксированных и уравнение (2.8) примет вид и будет выражать закон движения резания. Аналогично при фиксированном значении фиксируется и значение координаты . При фиксированных и 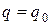уравнение (2.8) примет вид и будет выражать закон подачи инструмента. Если инструмент будет образовывать номинальную поверхность детали не режущей кромкой, а производящей поверхностью, то в уравнении (2.6) вместо одного параметра k будут два параметра - криволинейные координаты е и f производящей поверхности, и таким образом для этого инструмента число параметров, вид зависимостей которых от координат и можно выбрать, увеличивается на единицу.

По мере увеличения в схеме формообразования номинальной поверхности детали числа подач число параметров инструмента в правой части уравнения (3.6) увеличится, а следовательно, увеличится и число параметров, вид зависимости которых от координат и номинальной поверхности детали можно выбрать.

Выбор вида зависимости некоторого параметра -го движения от криволинейных координат и номинальной поверхности детали равносилен выбору вида зависимостей (2.4), которые определяют закон движения инструмента в системе координат .

Выбор вида зависимости криволинейных координат е и f производящей поверхности инструмента от криволинейных координат и равносилен выбору вида зависимости (2.3), т. е. выбору формы координатных линий е и f на производящей поверхности. Выбор вида зависимости параметра k формы режущей кромки от криволинейных координат и равносилен выбору вида зависимости (2.2), т. е. выбору формы режущей кромки.

Свобода в выборе формы режущей кромки, производящей поверхности или законов их движений облегчает создание оптимальной конструкции инструмента, как в технологическом, так и в эксплуатационном отношении. Однако кинематически сложные схемы формообразования не всегда отвечают требованиям высокой производительности обработки.

Существующие в настоящее время инструменты имеют сравнительно простые схемы формообразования и числа подачи, участвующие в формообразовании, в этих схемах в самых сложных случаях обработки не превышает трех. Часто поверхность резания совпадает с производящей поверхностью, поэтому максимальное число параметров инструмента, вид, зависимостей которых от координат и номинальной поверхности детали можно выбрать, для самых сложных случаев обработки не превышает двух-трех. Чаще же этот выбор ограничивается одним параметром, а в некоторых случаях такой выбор невозможен.

2.4.Формообразование номинальной поверхности детали режущей кромкой

Образование номинальной поверхности детали режущей кромкой инструмента осуществляется одним из следующих трех способов.

Рис. 2.8 – Обработка поверхности при двухпараметрическом огибании

1. Номинальная поверхность детали является огибающей двухпараметрического семейства поверхностей резания (параметры семейства — и подач). Ее две криволинейные координаты и зависят от четырех параметров инструмента — , , и . Вид, зависимости двух последних параметров от координат и выбирается при проектировании инструмента. Такой способ обработки имеет место при фрезеровании летучим резцом (фрезой с двусторонней режущей пластиной) рабочих поверхностей штампов для объемной штамповки (рис. 2.8): выбирается форма режущей кромки и закон движения резания; рассчитываются законы обеих подач (криволинейные координаты копиров или программа для ЧПУ, которые управляют инструментом). Летучий резец (фреза) вращается вокруг оси оправки. При этом в контакте с поверхностью детали при принятой глубине резания будет находиться участок режущей кромки , а кромка будет проходить в теле заготовки путь (см. рис. 2.6). Параметры и в зависимости от координат инструмента и формы поверхности, т. е. и будут переменными как в пространстве, так во времени. Подачи и определяются координатами криволинейной поверхности и , и рассчитываются исходя из параметров точности поверхности, например шероховатости, или параметров, определяемых динамикой процесса: жесткостью системы, стойкостью инструмента и др.

Рис. 2.9 – Твердосплавные неперетачиваемые пластины

В качестве режущего элемента инструментов, работающих по схеме двухпараметрического огибания, используются чаще всего неперетачиваемые пластины круглой формы с положительной геометрией передней и задней поверхностей (рис. 2.9).

а	в
б
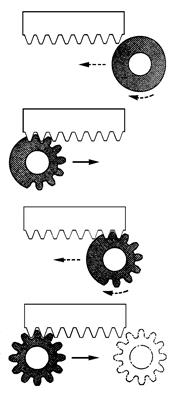
Рис. 2.10 – Зубонарезание гребенкой: а – прямозубого венца; б – косозубого венца; в – схема движений колеса в станочном зацеплении

2. Номинальная поверхность детали является огибающей однопараметрического семейства поверхностей резания (параметр семейства - параметр подачи). Две криволинейные координаты поверхности и зависят от трех параметров инструмента - , и Вид зависимости одного из параметров выбирается от и . Такой способ получения номинальной поверхности имеет место, например, при обработке зубчатых деталей зуборезной гребенкой (рис. 2.10).

Здесь выбирается закон подачи гребенки (величина радиуса начального цилиндра), а рассчитываются закон движения резания и форма режущей кромки гребенки.

3. Номинальная поверхность детали совпадает с поверхностью резания. Ее две криволинейные координаты и зависят от двух параметров инструмента и . Форма режущей кромки и закон движения предопределены формой криволинейных координат и . Такой способ формообразования имеет место, например, при затыловании фасонной фрезы затыловочным резцом (рис. 2.11).

Рис. 2.11 – Затылование червячной фрезы

Поверхность резания, описываемая режущей кромкой инструмента, в процессе обработки детали может менять свою форму, но может оставаться постоянной, «жесткой». В последнем случае ее можно уподобить производящей поверхности инструмента и при решении вопросов формообразования пользоваться расчетными зависимостями, выведенными для производящей поверхности. Например, при обработке зубчатых колес зуборезная гребенка, совершая возвратно-поступательные «долбящие» движения, своей режущей кромкой описывает поверхность резания, которая по форме является рейкой. Эта рейка положена в основу, как расчета самой гребенки, так и в основу решения вопросов формообразования гребенкой зубчатых деталей.

Режущие кромки, расположенные на производящей поверхности инструмента, при одном простом движении резания опишут семейство поверхностей резания. С точки зрения формообразования поверхность, огибающую это семейство поверхностей резания, можно рассматривать как поверхность, огибающую семейство производящих поверхностей, когда параметром семейства является параметр движения резания.

2.5. Формообразование номинальной поверхности детали режущей производящей поверхностью инструмента

Образование номинальной поверхности детали производящей поверхностью инструмента осуществляется одним из следующих способов.

1. Номинальная поверхность детали является огибающей семейства семейств поверхностей резания при трех подачах; производящая поверхность совпадает с поверхность резания. Криволинейные координаты и номинальной поверхности детали зависят от пяти параметров инструмента: формы координатных линий и производящей поверхности и параметров , , подач. Вид зависимостей от координат и трех параметров инструмента может быть выбран. Такой способ имеет место при обработке крупномодульных зубчатых колес фрезерной головкой, в которой группа дисковых фасонных фрез расположена так, что огибающая их поверхность является основным червяком, зацепляющимся с обрабатываемым зубчатым колесом. Режущий элемент (рис. 2.12, а) расположен на винтовой поверхности с параметром и перемещается с подачами и .

а	б	в
Рис. 2.12 – Формообразование с тремя подачами инструмента: а – элемент поверхности инструмента; б, в – направления подач инструмента

2. Номинальная поверхность детали является огибающей двухпараметрического семейства производящих поверхностей; параметры семейства - параметры и