 |
Алгоритм составления таблиц истинности
|
|
|
|
1. Найти количество строк в таблице: 2n, где n - количество переменных
2. Найти количество столбцов: количество переменных + количество логических операций.
3. Найти порядок выполнения логических операций.
4. Построить таблицу, указывая названия столбцов и возможные наборы значений исходных логических переменных.
пример:
Найти количество строк и столбцов таблицы истинности для логического высказывания: ((А 
В) → (В Ù С))↔ 
Решение:
Количество строк = 23=8
Количество столбцов = 3+5=8
Порядок действий:
1. А 
В
2. В Ù С
3. 1 → 2
4.
5. 3 ↔ 4
Составляем таблицу истинности:
| А | В | С | А В
| В Ù С | (А В) → (В Ù С)
|
| ((А  В) → (В Ù С))↔ 
|
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
Алгоритм упрощения формул с помощью равносильных преобразований
1. Заменить все "не базовые" операции (→, ↔, ⊕ и т.д.) на их выражения через базовые операции, Ù, 
.
2. Раскрыть инверсию сложных высказываний по законам де Моргана, чтобы операции инверсии остались только у отдельных переменных.
3. Использовать вынесение общего множителя за скобки, раскрыть скобки и другие законы алгебры логики, упростить выражение.
пример:
(А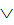 
В) Ù (
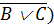Ù (АÙС) = (А 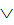В) Ù А Ù В Ù (АÙС) = (АÙА 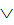ВÙА) Ù В Ù (А 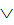С) = В Ù А Ù В Ù (А 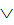С) = А Ù В Ù (А 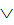С) = В Ù А Ù (А 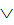С) = В Ù А.
В данном примере в последовательности были применены законы де Моргана: распределительный, исключение третьего, переместительный, повторение, и опять переместительный, а также закон поглощения.
Алгоритм перевода высказываний с естественного языка на формальный
|
|
|
1. Выделить и обозначить простые высказывания.
2. Найти логические связки и заменить их на соответствующие логические операции.
3. Записать логическую формулу сложного высказывания.
4. Сделать проверку на соответствие полученной формулы исходному высказыванию.
Алгоритм перевода высказывания с формального языка на естественный
1. Заменить логическую переменную простым высказыванием.
2. Логические операции заменить соответствующими логическими связками.
3. Составить предложение.
Используя перевод естественной речи на язык математической логики,
таблицы истинности, законы формальной логики в рассуждениях, а также теорию графов, можно решать текстовые задачи, встречающиеся в повседневной и профессиональной деятельности любого человека.
Высказывательная форма.
В математике часто встречаются предложения, содержащие одну или несколько переменных: х < 8, х + у = 10. Эти предложения не являются высказываниями, так как не имеет смысла вопрос, истинны они или ложны - это высказывательные формы.
пример: Предложение «Число х – двузначное» не является высказыванием, т.к. относительно него нельзя определить: истинно это предложение или ложно. Но при подстановке конкретных значений вместо переменной оно обращается в истинное или ложное высказывание. Например, при х=7 мы получим ложное высказывание «Число 7-двузначное», а при х=27 - истинное высказывание «Число 27-двузначное». Такое предложение называют предикатом или высказывательной формой.
Высказывание, которое содержит переменную, принимающую различные значения, причем подстановка любого из значений переменной превращает это предложение в высказывание, называется предикатом или высказывательной формой. Каждая высказывательная форма образует множество высказываний.
пример: при подстановке различных значений вместо переменной в высказывательную форму «х+2=10» получаем однотипные высказывания: 8+2=10, 7+2=10, 6+2=10 и др.
|
|
|
По числу переменных, входящих в высказывательную форму (предикат), их делят на одноместные, двухместные и т.д. и соответственно обозначают: А(х), В(х; у) и т.д.
пример: предложения «Число х - однозначное» и «х+4=10» являются одноместными высказывательными формами (предикатами), а предложения
«х > у» и «х + у =8» - двухместными высказывательными формами.
Для каждой высказывательной формы нужно указать множество значений, которые может принимать переменная (переменные), входящая в эту высказывательную форму.
Множество значений, которые может принимать переменная (переменные) высказывательной формы (предиката), называется областью определения высказывательной формы (предиката).
Область определения высказывательной формы будем обозначать через Х и предикаты будем записывать с указанием области определения: А(х), хÎХ; В(х; у), х, уÎХ и т.д. Запись А(х), х Î Х, читают: «Высказывательная форма (предикат) А(х) задана на множестве Х».
пример: 1. А(х): «Слово х - существительное», его областью определения будет множество слов русского языка.
2. В(х): «х+5=13», Х=R.
3. С(х): «Четырехугольник х - прямоугольник», Х - множество четырехугольников.
4. D(х; у): «х+у=7», Х=R или Х=N.
Среди всех возможных значений переменной из области определения выделяют те, которые обращают высказывательную форму в истинное высказывание.
Множество тех значений переменной из области определения высказывательной формы (предиката), при подстановке которых получаем истинные высказывания, называется множеством истинности высказывательной формы (предиката).
Множество истинности высказывательной формы (предиката) будем обозначать буквой Т. Тогда, согласно определению, ТÌХ (множество Т является подмножеством множества Х).
пример:
1. А(х): «Слово х - существительное», его множеством истинности является множество глаголов русского языка.
2. В(х): «х+8=13», Т={5}.
3. С(х): «Четырехугольник х - ромб», Т- множество ромбов.
4. D(х; у): «х+у=5». Множество истинности этого предиката может быть различным в зависимости от области определения. Если Х=R или Х=Z, то Т – множество пар чисел, сумма которых равна 5, причем это множество будет бесконечным. Если Х=N, то Т={(1;4), (2;3), (4;1), (3;2)}.
|
|
|
5. Q(х): «х<8», где хÎN, тогда Т={1;2;3;4;5;6;7}.
Высказывательную форму, заданную на конечном множестве, можно задавать таблицей, в первой строке которой указываются элементы области определения, а во второй – истинно или ложно высказывание, получаемое из высказывательной формы при подстановке этих элементов вместо переменной.
пример: пусть высказывательная форма А(х): «Число х - нечетно» задана на множестве Х={1; 2; 3; 4; 5; 6}. Так как высказывание «Число 2 - нечетно» ложно, то числу 2 будет соответствовать значение высказывательной формы «л» (ложь). Числу 1 соответствует истинное высказывание «Число 1- нечетно».
Следовательно, высказывательная форма обращается в высказывание при подстановке конкретных значений из области определения вместо каждой переменной, входящей в форму. Но высказывательную форму можно превратить в высказывание и другим способом.
|
|
|
