 |
Панель инструментов системы MATLAB.
|
|
|
|
MATLAB
Основы работы в MATLAB.
Рабочая среда MATLAB.
MATLAB – одна из самых мощных компьютерных систем, предназначенных для решения математических, инженерных и экономических задач. Входной язык системы MATLAB позволяет не только использовать встроенные команды, но и разрабатывать собственные визуальные приложения.
Окна системы MATLAB
Общение пользователя с системой MATLAB происходит посредством окон.
1. Command Window (Окно команд).
Окно Command Window является наиболее важным для пользователя. Посредством этого окна вводятся математические выражения, получаются результаты вычислений, а также выдаются сообщения, посылаемые системой. Математические выражения пишутся в командной строке после знака приглашения «>>». Например, наберем в командной строке 1+2
>> 1 + 2
Для выполнения действия нажмем клавишу «Enter».
В командном окне появится следующее
ans =
>> |
По умолчанию программа записывает результат в специальную переменную ans.
Выполним действие с использованием переменной и оператора присваивания «=». Для этого в командной строке набираем
>> z = 1.25 /3.11
z =
0.40193
Редактировать в Command Window можно только текущую командную строку. Для того чтобы отредактировать ранее введенную команду, необходимо установить курсор в строку ввода и воспользоваться клавишами «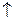
» или«
».
Командное окно можно закрыть кнопкой «
», а кнопка «» служит для отделения окна от интерфейса системы. Вернуться к стандартной форме окна можно с помощью меню:
Главное Меню → Desktop → Desktop Layout → Default.
(Главное Меню → Вид → Схема рабочего стола → По умолчанию).
Очистить командное окно можно с помощью меню:
Главное Меню → Edit → Clear Command Window.
|
|
|
(Главное Меню → Правка → Очистить командное окно).
2. Окно Workspace (Рабочая область).
Окно предоставляет пользователю список всех переменных, созданных в процессе работы. Можно выбрать любую переменную, просмотреть её содержимое или выполнить какие-либо другие действия. Для доступа нужно щелкнуть правой кнопкой мыши по имени переменной в списке.
3. Окно Current Folder (Текущий каталог).
Окно является аналогом известной программы Проводник. Окно служит для поиска, просмотра, открытия файлов и папок, осуществления смены текущей директории, установления пути к файлу и т.д.
4. Окно Command History (История команд).
Все команды, которые набираются в командной строке, автоматически образуют список, который выводится в окне Command History. Если появится необходимость повторить ранее выполненную команду, то она отыскивается в списке Command History, и, дважды щелкнув по ней левой кнопкой мыши, можно команду выполнить. Содержимое данного окна не теряется после выхода из системы и выключения компьютера. Удалить список команд можно только с помощью меню.
Главное меню системы MATLAB
Главное меню имеет стандартный вид и организацию, присущие многим программным продуктам. Главное меню MATLAB содержит следующие пункты:
File (Файл) – работа с файлами;
Edit (Правка) – редактирование;
Window (Окно) – связь с окнами системы;
Help (Справка) – связь со справочной системой MATLAB.
Панель инструментов системы MATLAB.
Кнопки панели инструментов имеют следующие назначения:
New file (Создать) – выводит окна редакторов файлов;
Open file (Открыть) – открывает окна загрузки файлов;
Cut (Вырезать) – вырезает выделенный фрагмент и помещает в буфер обмена;
Copy (Копировать) – копирует выделенный фрагмент в буфера обмена;
Paste (Вставить) – переносит выделенный фрагмент из буфера обмена в строку ввода;
Undo (Отменить) – отменяет результата предыдущей операции;
|
|
|
Redo (Повторить) – повторяет результат предыдущей операции;
Simulink – создает модель Simulink (расширения MATLAB);
Help (Помощь) – открывает окна справки.
Формат вывода результата вычислений
Числовые результаты могут быть представлены с плавающей точкой, (например 4.0193e-001, что означает 
), или с фиксированной точкой (например, 0.040193). Числа с плавающей точкой представлены в экспоненциальной форме
,
где 
– мантисса (целое или дробное число с десятичной точкой); 
– порядок (целое число).
Введем число 
в рабочую область.
При вводе вещественных чисел для отделения дробной части используется точка!
>> s = 0.3467819
В строке вывода появится число
s =
0.3468
Количество знаков в дробной части меньше, чем в строке ввода. Это происходит потому, что результат вычислений выводится в формате short (краткая запись числа), который определяется по умолчанию. Можно поменять формат на long (длинная запись числа), набрав команду
>> format long
>> s
s =
0.34678190000000
В списке Numerical Format также имеются форматы чисел
short e – краткая запись числа в формате с плавающей точкой;
long e – длинная запись числа в формате с плавающей точкой;
short g – вторая форма краткой записи числа в формате фиксированной точкой;
long g – вторая форма длинной записи числа в формате фиксированной точкой;
Информацию о форматах можно получить, набрав в командной строке
>> help format
Также формат отображения числовых данных можно установить в меню File (файл) пункт Preferences (предпочтения). Перейти на вкладку Command Window (окно команд). В опции Text display (отображение текста), в списке Numeric format (числовой формат) установить short g, в опции Numeric display (отображение чисел) установить compact. Эти форматы вывода соответствуют выводу чисел в универсальной форме из пяти значащих цифр и с подавлением пробела между строками.
Важно помнить, что, в каком бы формате не выводилось число, в памяти компьютера оно хранится со всеми введенными цифрами с погрешностью около 
(15 десятичных разрядов). Диапазон представления модуля действительного числа принадлежит интервалу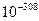 
до 
.
Основы работы в MATLAB.
Для выполнения простейших арифметических операций в MATLAB применяются операторы:
· сложение и вычитание +, –
· умножение и деление *, /
|
|
|
· возведение в степень ^
Для указания порядка выполнения арифметических операторов следует использовать круглые скобки.
Для определения переменной необходимо набрать её имя, символ «=» и значение переменной. Имя переменной не должно совпадать с именами встроенных переменных и функций. Система различает большие и малые буквы в именах переменных.
Некоторые специальные переменные:
ans – результат последней операции без знака присваивания;
eps – относительная погрешность при вычислениях с плавающей точкой;
realmax – наибольшее положительное число с плавающей точкой;
realmin – наименьшее положительное число с плавающей точкой;
pi – число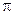 
;
i, j – мнимая единица;
Inf – бесконечность 
;
NaN – неопределенное значение.
Уничтожить одну или несколько переменных можно с помощью команды clear. Например,
>> x=3
x =
>> clear x
>> x
??? Не определенная функция или переменная 'x'.
Функции, используемые в MATLAB, можно разделить на встроенные и определенные пользователем.
Некоторые встроенные элементарные функции:
sin (x), cos (x), tan (x), cot (x) – синус, косинус, тангенс, котангенс числа x;
sec (x), csc (x) – секанс, косеканс числа x;
asin (x), acos (x), atan (x), acot (x) – арксинус, арккосинус, арктангенс, арккотангенс числа x;
exp (x) – экспонента числа x;
log (x) – натуральный логарифм числа x;
log10 (x) – десятичный логарифм числа x;
log2 (x) – логарифм по основанию 2 числа x;
pow2 (x) – возведение числа 2 в степень числа x;
sqrt (x)– квадратный корень из числа x;
abs (x) – модуль числа x;
round (x) – округление числа x до ближайшего целого;
fix (x) – округление числа x до ближайшего целого в сторону нуля;
floor (x) – округление числа x до ближайшего целого в сторону отрицательной бесконечности;
ceil (x) – округление числа x до ближайшего целого в сторону положительной бесконечности;
mod (x,y) – остаток от целочисленного деления x на y с учетом знака;
rem (x,y) – остаток от целочисленного деления x на y;
sign (x) – возвращение знака числа x.
Вычислим значение выражение
>> exp(–2.5)*log(11.3)^0.3 – sqrt((sin(2.45*pi)+cos(3.78*pi))/tan(3.3))
ans =
–3.2105
Затем вычислим значение похожего выражения:
|
|
|
Для этого необязательно снова набирать его в командной строке. Для вычисления этого выражения, надо проделать шаги:
- Нажать клавишу «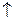», при этом в командной строке появиться ранее введенное выражение;
- внести необходимые изменения в операциях;
- нажать «Enter».
>> exp(–2.5)*log(11.3)^0.3 + ((sin(2.45*pi)+cos(3.78*pi))/tan(3.3))^2
ans =
121.2446
Если оператор не удается разместить в одной строке, то возможно продолжение его ввода в следующей строке, если в конце первой строки указать знак продолжения «…», например, предыдущий пример можно выполнить в виде
>> exp(–2.5)*log(11.3)^0.3 +...
((sin(2.45*pi)+cos(3.78*pi))/tan(3.3))^2
ans =
121.2446
Найти значение выражения
>> x = sin(1.3*pi)/log(3.4);
>> y = sqrt(tan(2.75)/ cot(2.3));
>> z = (x+y)/(x-y)
z =
-0.013967
Знак «;» в конце строки означает подавления вывода на экран промежуточных значений.
Используя переменные x и y, найдем значение выражения
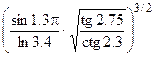
>> t = (x*y)^(3/2)
t =
-5.5344e-017 - 0.30128i
Большинство математических функций MATLAB предусматривает работу с комплексными аргументами.
Введем комплексное число 
:
>> z = 3 + 4i
z =
3.0000 + 4.0000i
Для вычисления комплексно-сопряженного числа применяется апостроф «’».
>> z1 = z'
z1 =
3.0000 - 4.0000i
Функции для работы с комплексными числами:
abs (z), angle (z) – модуль 
и аргумент 
комплексного числа 
, где 
, 
;
complex( a, b ) – конструирует комплексное число по его действительной и мнимой части:
>> complex(2.3, 5.8)
ans =
2.3 + 5.8i
conj (z)– возвращает комплексно-сопряженное число;
imag (z), real (z) – возвращает мнимую и действительную часть комплексного числа.
3. Векторы.
Ввод, сложение, вычитание, умножение на число.
Вектор в MATLAB формируется с помощью оператора квадратные скобки [ ]. При этом элементы вектора - столбца разделяют точкой с запятой «;», а элементы вектора – строки разделяют пробелом «» или запятой «,».
Введем вектор-столбец 
.
>> x = [1.3; 5.4; 6.9]
x =
1.3
5.4
6.9
Введем вектор-строку 
.
>> y = [7.1 3.5 8.2]
y =
7.1 3.5 8.2
Для транспонирования вектора применяют апостроф «’»:
>> z = y’
z =
7.1
3.5
8.2
Для нахождения суммы и разности векторов используются знаки «+» и «–»:
>> с = x + z
c =
8.4
8.9
15.1
Умножение вектора на число осуществляется как справа, так и слева при помощи знака «*».
>> t = 3*x
t =
3.9
16.2
20.7
Векторы могут быть аргументами встроенных функций, например,
>> d = sin(c)
d =
0.8546
0.50102
0.5712
Для обращения к элементам векторов используется индексация, например,
>> h = x(2)
h =
5.4
Из элементов вектора можно составить новый вектор, например
>> g = [x(2) x(3) x(1)]
g =
5.4 6.9 1.3
Из нескольких векторов-столбцов можно составить один, например
>> t = [x; z]
t =
1.3
5.4
6.9
7.1
3.5
8.2
Из нескольких векторов-строк можно составить одну строку, например
|
|
|
>> r = [x’ y]
r =
1.3 5.4 6.9 7.1 3.5 8.2
Символ двоеточие «:» используется для выделения элементов из вектора
>> w = r(3:5)
w =
6.9 7.1 3.5
Символ двоеточие «:» также позволяет заменять элементы вектора, например,
>> r(3:5)= 0
r =
1.3 5.4 0 0 0 8.2
Символ «:» также можно использовать для построения вектора, каждый элемент которого отличается от предыдущего на постоянное число, т.е. шаг, например
>> h = [1:0.2:2]
h =
1 1.2 1.4 1.6 1.8 2
Шаг может быть отрицательным (в этом случае начальное число должно быть больше конечного).
Шаг, равный единице, можно не указывать
>> k = [1:5]
k =
1 2 3 4 5
Поэлементные операции с векторами.
Операции «.*», «.^», «./» приводят к поэлементному умножению, поэлементному возведению в степень, поэлементному делению двух векторов.
Для того чтобы, к каждому элементу вектора прибавить одно и тоже число используется знак «+», для вычитания из элементов вектора одного и того числа используется знак «–».
Разделить элементы вектора на число можно при помощи знака «/».
Деление числа на вектор, осуществляется с помощью операции «./».
Пример.
Даны векторы
, 
, 
, 
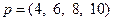Выполните команды, опуская знак «;» в конце выражения.
>> v1 = [2 –3 4 1];
>> v2 = [7 5 –6 9];
>> p = [4 6 8 10];
>> f = [4 2 6];
>> s1 = v1.*v2;
>> s2 = v1.^2;
>> s3 = v1.^v2;
>> s4 = v1./v2;
>> a = p + 1.2;
>> b = p – 1.2;
>> p = p/2;
>> df = 12./f;
Основные функции для работы с векторами.
- length( z ) – определение длины вектора;
- prod( z ) – перемножение всех элементов вектора;
- sum( z ) – суммирование всех элементов вектора;
- mean( z ) – вычисление среднего арифметического элементов вектора;
- sort( z ) – упорядочение вектора по возрастанию его элементов;
- max( z ) – нахождение максимального элемента;
- min( z ) – нахождение минимального элемента.
Если вызвать функцию min или max с двумя выходными аргументами [m, k] = min(z),
то первой переменной присваивается значение минимального (максимального элемента), а второй переменной присваивается номер этого элемента.
Пример.
Дан вектор
,
Выполните команды, опуская знак «;» в конце выражения.
>> z = [3; 2; 1; 4; 6; 5];
>> l = length(z);
>> p = prod(z);
>> s = sum(z);
>> q = mean(z);
>> M = max(z);
>> m = min(z);
>> [m, k] = min(z);
>> sr = sort(z);
4. Матрицы.
Различные способы ввода матрицы.
1. Матрицу можно вводить как вектор-столбец, состоящий из двух элементов, каждый из которых является вектор - строкой и отделяется точкой с запятой. Например, введем матрицу
>> A = [3 1 –1; 2 4 3 ]
A =
3 1 –1
2 4 3
2. Матрицу можно вводить построчно, выполняя последовательность команд:
>> A = [3 1 –1
«Enter»
2 4 3]
«Enter»
В результате получим ту же матрицу.
3. Матрицу можно составить из блоков, например
>> A = [ [3;2] [1;4] [-1;3]]
или
>> A = [ [3 1;2 4] [-1;3]]
Доступ к элементам матрицы осуществляется при помощи двух индексов – номеров строки и столбца:
>> A (2, 3)
ans =
Создание матриц специального вида.
Функция
- zeros (m,n) формирует нулевую матрицу размера
; - eye (n) формирует единичную матрицу размера
; - ones (m,n) формирует матрицу размера из единиц;
- rand (m,n) создает матрицу размера из случайных чисел.
Пример.
Выполните команды, опуская знак «;» в конце выражения.
>> O = zeros(3, 6);
>> E = eye(4);
>> E = eye(8,4);
>> EI = ones(3, 8);
>> R = rand(3,5)
Функция diag (d) формирует диагональную матрицу из вектора d, например
>> d = [1; 2; 3; 4];
>> D = diag(d)
D =
1 0 0 0
0 2 0 0
0 0 3 0
0 0 0 4
Функция diag( A ) служит также для выделения диагонали матрицы A в вектор, например
>> A = [10 1 2; 1 20 3; 2 3 30];
>> d = diag(A)
d =
Выделение блоков и заполнение матрицы при помощи индексации.
Символ двоеточие «:» используется для выделения блоков из матрицы.
Представляется в следующих формах:
- M(i,:) – выбирается i-я строка из матрицы M;
- M(:, j) – выбирается j-й столбец из матрицы M;
- M(:) – представление матрицы M в виде столбца;
- M(k:l, n:m) – выбирается блок из матрицы M, ограниченный элементами
, 
, 
, 
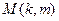; - Команда M(k:l, n:m) = число заменяет элементы блока матрицы M;
- Команда M(i,:) = [] удаляет i-ю строку из матрицы M;
- Команда M(:, j) = [] удаляет j-й столбец из матрицы M;
Пример.
Дана матрица
Выполните команды, опуская знак «;» в конце выражения.
>> P = [5 2 1 3; 3 -1 1 2; 1 2 4 8; 3 -1 1 2];
>> P1 = P(2:3, 2:3);
>> P(2:3,2:3)=0;
>> st = P(2,:);
>> rt = P(2, 2:end);
>> P(1,:) = [];
Пример.
Создать матрицу 
.
Для этого применяем последовательность команд
>> T = zeros(5);
>> T(1,:) = 1;
>> T(end, 3:end) = –1
T =
1 1 1 1 1
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 –1 –1 –1
Действиями с матрицами и элементами матриц.
Транспонирование матрицы из действительных чисел осуществляется с помощью апострофа «’».
Сложение и вычитание матриц одного размера осуществляется при помощи знаков «+» и
«–».
Для умножения согласованных матриц используется знак «*». Этот же знак используется для произведения матрицы на число.
Возведение квадратной матрицы в целую степень производится с использованием оператора «^».
Операторы «.*», «./», «.^» служат для умножения, деления, возведения в степень каждого элемента одной матрицы на соответствующий элемент другой матрицы. Символы «.^» служит также для возведения каждого элемента матрицы в степень.
Пример.
Даны матрицы
и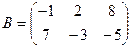 
.
Выполните команды, опуская знак «;» в конце выражения.
>> A = [2 5 –1; 3 4 9];
>> B = [–1 2 8; 7 –3 –5];
>> S = A+B;
>> R = A – B;
>> A’;
>> D = A*A’;
>> D1 = D*3;
>> С = A.*B;
>> Q = A./B;
>> P = A.^B;
>> D = A.^2;
Некоторые функции для работы с матрицами.
Функция
- size( M ) определяет размер матрицы M;
- sum( M ) суммирует элементы матрицы M по столбцам;
- sum( M, 2 ) суммирует элементы матрицы M по строкам;
- prod( M ) находит произведения элементов матрицыM по столбцам;
- prod( M,2 ) находит произведения элементов матрицыM по строкам;
- sort( M ) упорядочивает элементы каждого столбца матрицы M в порядке возрастания;
- sort( M, 2 ) упорядочивает элементы каждой строки матрицы M в порядке возрастания;
- max( M ) формирует вектор - строку, содержащую максимальные элементы в столбцах матрицы M;
- min( M ) формирует вектор - строку, содержащую минимальные элементы в столбцах матрицы M;
- max (M, [], 2) формирует вектор - столбец, содержащий максимальные элементы в строках матрицы M;
- min (M, [], 2) формирует вектор - столбец, содержащий минимальные элементы в строках матрицы M;
- rot90 (M) осуществляет поворот матрицы M на
; - tril (M) формирует из матрицы M нижнюю треугольную матрицу, начиная с главной диагонали;
- triu (M) формирует из матрицы M верхнюю треугольную матрицу, начиная с главной диагонали;
Пример.
Дана матрица
.
Выполните команды, опуская знак «;» в конце выражения.
>> M = [1 –2 –4; 3 –6 4; 2 –2 0];
>> SZ = size(M);
>> S = sum(M);
>> S2 = sum(M, 2);
>> P = prod(M);
>> P2 = prod (M,2);
>> mx = max(M);
>> mn = min(M);
>> MX = max(M, [], 2);
>> MN = min(M, [], 2);
Операции отношения и логические операции.
Операторы отношения производят поэлементное сравнение двух матриц и возвращают матрицу той же размерности с элементами 1, где отношение истинно и 0, где отношение ложно:
< – меньше чем (<= означает "меньше или равно");
> – больше чем (>= означает "больше или равно").
Логические операции осуществляются с помощью операторов:
= = – логический оператор эквивалентности;
& – логическое "И".
A & B – это матрица, элементы которой равны 1, если соответствующие элементы и A и B ненулевые, иначе равны 0;
| – логическое "ИЛИ".
A | B – это матрица, элементы которой равны 1, если соответствующие элементы или A или B ненулевые, иначе равны 0;
~= – логическое дополнение "НЕ" (~= означает не "равно").
Пример.
Даны матрицы
, 
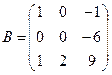
Выполните команды, опуская знак «;» в конце выражения.
>> A = [1 2 3; 4 0 6; 7 1 9];
>> В = [1 0 -1; 0 0 -6; 1 2 9];
>> D1 = A>B;
>> D2 =A<=B;
>> D3 = A&B;
>> D4 = A==B;
|
|
|
