 |
Функции, задаваемые пользователем
|
|
|
|
Рассмотрим два способа задания функций, определенных пользователем, в MATLAB.
Первый способ использует оператор @ для создания, так называемой «анонимной функции».
Второй способ использует команду inline.
Рассмотрим два способа на примере функции одной переменной
.
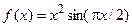Как было отмечено ранее, большинство функций MATLAB могут оперировать как векторами, так и скалярами, и чтобы быть уверенным, что в качестве аргумента функции может выступать вектор, необходимо ставить точки перед математическими операциями ^, *.
Первый способ:
>> f = @(x) x.^2.*sin(pi*x/2)
f =
@(x)x.^2.*sin(pi*x/2)
Второй способ:
>> f1 = inline('x.^2.*sin(pi*x/2)')
f1 =
Inline function:
f1(x) = x.^2.*sin(pi*x/2)
Когда функция задана, неважно каким методом, её можно вычислить, например
>> a = f(3)
a =
-9
>> a = f1(3)
a =
-9
или
>> x = [1 2 3]
x =
1 2 3
>> a = f(x)
a =
1.0000 0.0000 -9.0000
>> a = f1(x)
a =
1.0000 0.0000 -9.0000
Этими способами можно задать функцию двух и более аргументов.
Например, 
.
>> g = @(x,y) (x+y).*exp(x)
g =
@(x,y)(x+y).*exp(x)
>> g1 = inline('(x+y).*exp(x)','x','y')
g1 =
Inline function:
g1(x,y) = (x+y).*exp(x)
>> x = [1 2]
x =
1 2
>> y = [2.5 3.4]
y =
2.5000 3.4000
>> u = g(x,y)
u =
9.5140 39.9009
>> u = g1(x,y)
u =
9.5140 39.9009
Создание М-файлов.
М-файл позволяет вводить большое число команд, изменять их, создавать собственные функции.
Для создания М-файла открываем меню File основного окна MatLab и в пункте New выбираем подпункт M-file. На экране открывается новое окно редактора М-файлов.
Набираем в этом окне команды, например, создаем из двух матриц одну расширенную.
------------------------------------------------------------------------------------------------------------------------
A = [2 1 -0.1 1
0.4 0.5 4 -8.5
0.3 -1 1 5.2
1 0.2 2.5 -1]
B = [2.7; 21.9; -3.9; 9.9]
D = [A B]
-----------------------------------------------------------------------------------------------------------------------
|
|
|
Сохраним файл с именем, например, proba в личном каталоге, выбирая при этом пункт Save as меню File редактора. Для запуска на выполнение всех команд М-файла, следует выбрать пункт Run в меню Debug (или нажать F5).
Отдельные блоки М-файла можно снабжать комментариями, которые начинаются со знака процента %. Например, редактируем уже существующий файл:
------------------------------------------------------------------------------------------------------------------------
% Создание матрицы А
A = [2 1 -0.1 1
0.4 0.5 4 -8.5
0.3 -1 1 5.2
1 0.2 2.5 -1];
% Создание матрицы В
B = [2.7; 21.9; -3.9; 9.9];
% Создание расширенной матрицы D
D = [A B];
% Вывод матрицы D на экран в командное окно
disp('Расширенная матрица D = ')
disp(D)
------------------------------------------------------------------------------------------------------------------------
Сохраним и запустим снова этот файл.
Вывод результата и текста в командное окно осуществляется оператором disp, причем текст указывается в апострофах.
Открытие уже существующего М-файла осуществляется при помощи пункта Open меню File, либо редактора М-файлов.
7. Создание М-функций.
Файл-функции с одним входным аргументом.
Если в вычислениях часто используется некоторая функция 
, то имеет смысл один раз написать файл-функцию, а потом вызывать её, всюду, где это необходимо. Например, требуется создать функцию
.
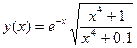Для этого открываем новый М-файл и набираем текст
------------------------------------------------------------------------------------------------------------------------
function f = myfun(x)
f = exp(-x).*sqrt((x.^4 + 1)./(x.^4 + 0.1));
-----------------------------------------------------------------------------------------------------------------------
Слово function в первой строке определяет, что данный файл содержит файл-функцию; myfun – имя функции; x – входной аргумент; f – выходной аргумент. Затем идет тело функции, которое состоит, в данном примере, из одной строки. Вообще, тело функции может состоять из нескольких строк, важно, чтобы окончательное значение функции записывалось в f.
В конце ставиться «;» для подавления вывода лишней информации на экран.
|
|
|
Сохраняем файл под именем функции myfun.
Теперь созданную функцию можно использовать так же, как и встроенные функции sin, cos, и другие. Например, наберем в командной строке
>> y = myfun(1.3)
y =
0.3113
При создании функции использовались поэлементные операции, следовательно, её входным аргументом могут быть векторы, например, наберем в командной строке:
>> x = [1.3 7.2];
>> y = myfun(x)
y =
0.3113 0.0007
Файл-функции с несколькими входными аргументами.
Напишем файл-функцию, вычисляющую длину радиус-вектора точки
.
Написание файл-функции с несколькими входными аргументами практически не отличается от случая с одним аргументом. Все входные аргументы размещаются в списке через запятую:
------------------------------------------------------------------------------------------------------------------------
function r = radius3(x, y, z)
r = sqrt(x.^2 + y.^2 + z.^2);
------------------------------------------------------------------------------------------------------------------------
Сохраним эту функцию под именем radius3. Затем, в командной строке наберем:
>> R = radius3(1, 1, 1)
R =
1.732
Файл-функции с несколькими выходными аргументами.
Файл-функции с несколькими выходными аргументами удобны при вычислении вектор-функций. Выходные аргументы добавляются через запятую в список входных аргументов, а сам список заключается в квадратные скобки. Например, вычислим функцию, переводящее время, заданное в секундах, в часы, минуты и секунды.
-----------------------------------------------------------------------------------------------------------------------
function [h, m, s] = hms(sec)
h = floor(sec/3600);
m = floor((sec-h*3600)/60);
s = sec – h*3600 – m*60;
------------------------------------------------------------------------------------------------------------------------
При вызове файл-функции с несколькими выходными аргументами результат следует записать в вектор:
>> [H, M, S] = hms(10000)
H =
M =
S =
Если список входных и выходных аргументов пуст, то заголовок выглядит так
function funname() или function [] = funname().
|
|
|
