 |
Получите у преподавателя допуск для выполнения измерений.
|
|
|
|
ИЗМЕРЕНИЯ:
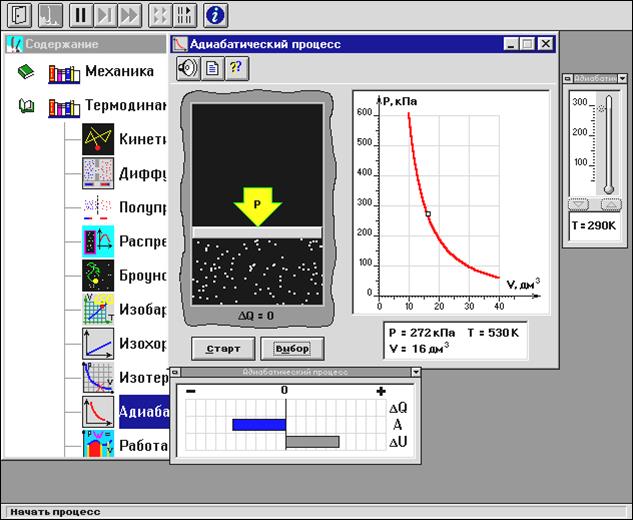
Установите начальное значение объема Vнач = 40 дм3 и начальную температуру Т1 газа, близкую к числам из табл.1. Для этого нажмите кнопку «ВЫБОР», переместите маркер мыши так, чтобы его острие находилось в указанной точке вблизи границы столбика на градуснике, и коротко нажмите и удерживая левую кнопку мыши двигайте столбик.
Нажмите мышью кнопку «Старт» на экране и наблюдайте перемещение поршня на левой картинке модели и перемещение точки по красной кривой теоретической адиабаты. Попробуйте останавливать процесс нажатием кнопки «СТОП». Последующий запуск процесса осуществляется нажатием кнопки «Старт».
После автоматической остановки процесса запустите его снова, нажав кнопку «Старт», и останавливайте, нажимая кнопку «Стоп», когда крестик на теоретической адиабате (красная кривая) будет находиться вблизи следующих значений объема: 15, 20, 25, 30, 35 и 40 дм3 (6 значений), записывая при остановке значения объема, температуры и давления в таблицу 2.
Установите новое значение температуры Т2, взяв его из таблицы 1, задавая Vнач = 40 дм3 и повторите измерения, записывая результаты в таблицу 3.
ТАБЛИЦА 1. Начальные значения температуры (не перерисовывать)
| Бригада | ||||||||
| Т1 | ||||||||
| Т2 |
ТАБЛИЦЫ 2,3 Результаты измерений
| Т[К] | ||||||
| V[дм3] | ||||||
| p[кПа] |
ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЕТА:
Постройте на одном рисунке графики экспериментальных зависимостей логарифма давления от логарифма объема для обеих адиабат (указав на них начальные температуры).
|
|
|
Для каждой адиабаты определите по графику экспериментальное значение показателя, используя формулу  .
.
Определите число степеней свободы молекулы газа, исследуемого в данной компьютерной модели, используя формулу (2).
Подберите распространенный газ, структура молекулы которого близка к наблюдаемой.
Запишите ответы и проанализируйте ответы и графики.
Вопросы и задания для самоконтроля
1. Что такое параметры состояния системы?
2. Дайте определение равновесного состояния системы.
3. Какой процесс называется обратимым?
4. Что такое цикл?
5. Что такое уравнение состояния?
6. Для какого физического газа можно применить модель «идеальный газ»?
7. Какому уравнению подчиняется состояние идеального газа? Напишите его.
8. Дайте определение теплоемкости тела.
9. Дайте определение удельной теплоемкости.
10. Напишите формулу для теплоемкости при постоянном объеме.
11. Напишите формулу для теплоемкости идеального газа при постоянном давлении.
12. Что такое число степеней свободы? Чему оно равно для одноатомной молекулы?
13. Что такое показатель адиабаты?
14. Напишите формулу связи показателя адиабаты с числом степеней свободы молекулы идеального газа.
15. Дайте определение адиабатического процесса.
16. Напишите уравнение адиабатического процесса.
17. Дайте определение изопроцесса. Перечислите известные изопроцессы.
18. Напишите уравнение и нарисуйте PV-диаграмму изотермического процесса.
19. Напишите уравнение и нарисуйте PV-диаграмму изобарического процесса.
20. Напишите уравнение и нарисуйте PV-диаграмму изохорического процесса.
ЛАБОРАТОРНАЯ РАБОТА № 4_2
РАСПРЕДЕЛЕНИЕ МАКСВЕЛЛА
Ознакомьтесь с теорией в конспекте и учебнике (Савельев, т.1, §93,98,99).
Выберите «Термодинамика и молекулярная физика», «Распределение Максвелла». Нажмите кнопку с изображением страницы во внутреннем окне. Прочитайте теорию и запишите необходимое в свой конспект лабораторной работы. Закройте окно теории, нажав кнопку с крестом в правом верхнем углу внутреннего окна.
|
|
|
ЦЕЛЬ РАБОТЫ:
* Знакомство с компьютерной моделью, описывающей поведение молекул идеального газа
* Экспериментальное подтверждение распределения Максвелла молекул идеального газа по скоростям.
* Экспериментальное определение массы молекул в данной модели.
КРАТКАЯ ТЕОРИЯ:
ВЕРОЯТНОСТЬЮ Рi получения некоторого результата измерения называется предел отношения количества измерений, давших этот результат, (Ni) к полному числу измерений N, когда N ® ¥.
ЭЛЕМЕНТАРНОЙ вероятностью dPV при измерении величины скорости v называется вероятность наличия скорости величиной от v до v + dv. Эта вероятность пропорциональна приращению скорости dv: dPV = F(v) dv, где коэффициент пропорциональности F(v) называется ФУНКЦИЕЙ РАСПРЕДЕЛЕНИЯ молекул по величине скорости. Она может быть выражена через другие функции распределения
F(v) = j(vX)×j(vY)×j(vZ)×4pv2 = f(v)×4pv2, где j(vX), ×j(vY) и×j(vZ) - функции распределения для соответствующих проекций скоростей молекул, а f(v) - их произведение.
В §98 вы можете найти вывод формул, в частности
 .
.
СреднЯЯ скорость  ,
,
СреднЯЯ квадратичная скорость vср.кв =  .
.
Наивероятнейшей называется скорость vВЕР, при которой F(v) имеет максимум:
vВЕР =  .
.
|
|
|


