Методика и порядок измерений

Внимательно рассмотрите рисунок и зарисуйте необходимое в свой конспект лабораторной работы.

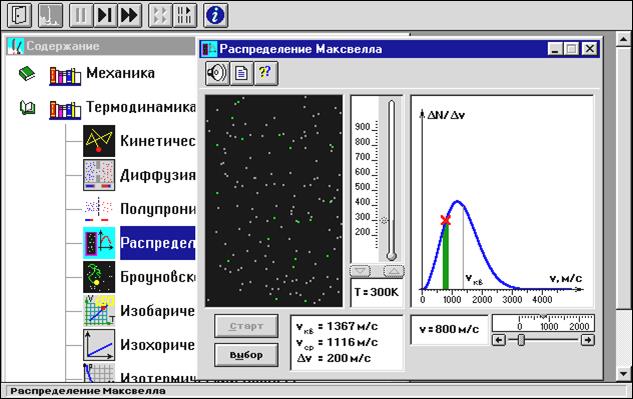
Внимательно рассмотрите изображение на экране монитора компьютера. Обратите внимание на систему частиц, движущихся в замкнутом объеме слева во внутреннем окне. Они абсолютно упруго сталкиваются друг с другом и со стенками сосуда. Их количество около 100 и данная система является хорошей «механической» моделью идеального газа. В процессе исследований можно останавливать движение всех молекул (при нажатии кнопки «çê» вверху) и получать как бы «мгновенные фотографии», на которых выделяются более ярким свечением частицы (точки), скорости которых лежат в заданном диапазоне Dv вблизи заданной скорости v (т.е., имеющие скорости от v до v+Dv). Для продолжения наблюдения движения частиц надо нажать кнопку «uu». Запишите в тетрадь значение Dv, указанное на экране.

Получите у преподавателя допуск для выполнения измерений.

ИЗМЕРЕНИЯ

1. Нажмите кнопки «uu», «СТАРТ» и «ВЫБОР» и установите температуру Т₁, указанную в таблице 1 для вашей бригады. Запишите для нее значение наивероятнейшей скорости.

2. Установите скорость выделенной группы молекул вблизи минимального заданного в таблице 2 значения.

3. Нажмите клавишу «çê» и подсчитайте на «мгновенной фотографии» количество молекул DN, скорости которых лежат в заданном диапазоне Dv вблизи заданной скорости молекул v (они более яркие). Результат запишите в таблицу 2.

4. Нажмите кнопку «uu» и через 10-20 секунд получите еще одну мгновенную фотографию (нажав кнопку «çê»). Подсчитайте количество частиц с заданной скоростью. Результат запишите в табл.2.

5. Повторите еще 3 раза измерения для данной скорости и результаты запишите в табл.2.

6. Измените скорость до значения, указанного в табл.2, и сделайте по 5 измерений (как в пункте 4) для каждой скорости.

7. Установите (как в пункте 1) вторую температуру Т₂ из табл.1. Запишите для нее значение наивероятнейшей скорости.

8. Повторите измерения (по пунктам 2,3,4,5), записывая результат в табл.3, аналогичную табл.2.

ТАБЛИЦА 1. Примерные значения температуры (не перерисовывать)

Бригада
Т1
Т2

ТАБЛИЦЫ 2,3 Результаты измерений при T = ____ K

v[км/с]=	0.5	1.0	1.5	2.0	2.5	3.0	3.5
DN1
DN2
DN3
DN4
DN5
DNСР

ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЕТА:

Вычислите и запишите в таблицы средние значения количества частиц DN_ср, скорости которых лежат в данном диапазоне от v до v+Dv.

Постройте на одном рисунке графики экспериментальных и теоретических зависимостей DN_ср(v). Теоретические зависимости можно срисовать с экрана монитора компьютера, подобрав соответствующий масштаб по вертикальной оси ординат.

Для каждой температуры определите экспериментальное значение наивероятнейшей скорости молекул v_вер.

Постройте график зависимости квадрата наивероятнейшей скорости от температуры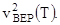

По данному графику определите значение массы молекулы

.

Подберите газ, масса молекулы которого достаточно близка к измеренной массе молекулы.

Запишите ответы и проанализируйте ответы и графики.

 

Табличные значения

Газ	Водород	Гелий	Неон	Азот	Кислород
Масса молекулы 10-27 кг	3.32	6.64	33.2	46.5	53.12

Вопросы и задания для самоконтроля

 

1. Дайте определение вероятности получения некоторого результата измерения.

2. Дайте определение элементарной вероятности при измерении величины скорости.

3. Что такое функция распределения?

4. Как связаны функции распределения величины и проекции скорости?

5. Каковы особенности графика функции распределения величины скорости молекул идеального газа?

6. Как вычисляется среднее значение некоторой физической величины А, если известна ее функция распределения f(A)?

7. Напишите формулу для вычисления среднего значения скорости молекул.

8. Напишите формулу для вычисления средней квадратичной скорости молекул.

9. Напишите условие для вычисления наивероятнейшей скорости молекул.

10. Напишите выражение для средней скорости молекул идеального газа.

11. Напишите выражение для средней квадратичной скорости молекул идеального газа.

12. Напишите выражение для наивероятнейшей скорости молекул идеального газа.

13. Вычислите на сколько процентов отличаются средняя и средняя квадратичная скорости молекул идеального газа.

14. Вычислите на сколько процентов отличаются средняя и наивероятнейшая скорости молекул идеального газа.

 

ЛАБОРАТОРНАЯ РАБОТА № 4_3

ДИФФУЗИЯ В ГАЗАХ

 

Ознакомьтесь с теорией в конспекте и учебнике (Савельев, т.1, §128, §130).

Выберите «Термодинамика и молекулярная физика», «Диффузия». Нажмите кнопку с изображением страницы во внутреннем окне. Прочитайте теорию и запишите необходимое в свой конспект лабораторной работы. Закройте окно теории, нажав кнопку с крестом в правом верхнем углу внутреннего окна.

ЦЕЛЬ РАБОТЫ:

* Знакомство с компьютерной моделью, описывающей диффузию молекул идеального газа

* Экспериментальное подтверждение закона диффузии.

* Экспериментальное определение средней скорости теплового движения частиц в данной модели.

КРАТКАЯ ТЕОРИЯ:

При нарушении равновесия макросистема стремится вернуться в равновесное состояние.

ЯВЛЕНИЯМИ ПЕРЕНОСА называются процессы, связанные с возникновением в веществе НАПРАВЛЕННОГО ПЕРЕНОСА (потока) массы, импульса или внутренней энергии.

ДИФФУЗИЯ есть процесс установления внутри фаз вещества равновесного распределения концентраций, который обеспечивается направленным переносом массы этого вещества. Диффузия обусловлена тепловым движением молекул и проявляется в самопроизвольном выравнивании концентраций в смеси нескольких веществ.

САМОДИФФУЗИЯ имеет место при самопроизвольном выравнивании концентрации однородного вещества, если по некоторым причинам равновесное распределение концентрации было нарушено.

ДЛИНА СВОБОДНОГО ПРОБЕГА l есть среднее расстояние, пролетаемое частицей между двумя последовательными столкновениями. Эффективный диаметр частицы есть минимальное расстояние, на которое сближаются центры двух сталкивающихся частиц.

Если в начальный момент времени имеет место неоднородное распределение плотности вещества r вдоль только одной оси (например, ОХ), тогда возникает одномерная диффузия, связанная с переносом массы М вдоль этой оси ОХ. Для двухкомпонентной системы (например, смеси двух газов) одномерная диффузия описывается первым законом Фика:

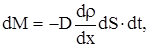
где dM - масса одного компонента (индексы для характеристик данного компонента пропущены), которая переносится за время dt через элементарную площадку, перпендикулярную оси ОХ, имеющую площадь dS, в направлении убывания плотности этого компонента, градиент плотности первого компонента, D - коэффициент диффузии.

Для смеси «красных» и «зеленых» частиц, имеющих одинаковую массу m каждой частицы, dM = m·dN, r = m 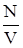, а , где dN - количество частиц, проходящих через dS за время dt, которое равно , где разность числа частиц в левом и правом сосудах DN = N₂ - N₁ , N₂ = N₀ - N(t), N₁ = N(t), DX = L_отв, объем сосуда V = 20 cм³, dS есть площадь отверстия. Решаем уравнение методом разделения переменных:

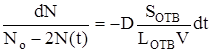. Интегрируем слева от 0 до N(t), а справа - от 0 до t и получаем:

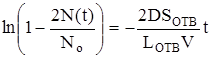или .

 

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: