 |
Некоторые важные замечания к формуле разложения
|
|
|
|
- При наличии в цепи синусоидальной ЭДС
для перехода от комплекса к функции времени от правой части формулы разложения берется мнимая часть, т.е. выражение при j. Если при этом в цепи также имеют место другие источники, например, постоянной Е и экспоненциальной 
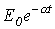ЭДС, и начальные условия для токов в ветвях с индуктивными элементами и напряжений на конденсаторах ненулевые, то они должны быть все введены в формулу предварительно умноженными на j, поскольку только в этом случае они будут учтены при взятии мнимой части от формулы разложения, т.е.
.
- Принужденной составляющей от действия источника синусоидальной ЭДС в формуле разложения соответствует слагаемое, определяемое корнем
. Для сложных схем такое ее вычисление может оказаться достаточно трудоемким, в связи с чем принужденную составляющую в этих случаях целесообразно определять отдельно символическим методом, а свободную – операторным. - Комплексно-сопряженным корням уравнения
в формуле разложения соответствуют комплексно-сопряженные слагаемые, которые в сумме дают удвоенный вещественный член, т.е. для к-й пары комплексно-сопряженных корней имеет место
.
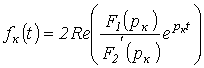Последовательность расчета переходных процессов
операторным методом
1. Определение независимых начальных условий путем расчета докоммутационного режима работы цепи.
2. Составление операторной схемы замещения цепи (для простых цепей с нулевыми начальными условиями этот этап может быть опущен).
3. Запись уравнений по законам Кирхгофа или другим методам расчета линейных цепей в операторной форме с учетом начальных условий.
4. Решение полученных уравнений относительно изображений искомых величин.
|
|
|
5. 
Определение оригиналов (с помощью формулы разложения или таблиц соответствия оригиналов и изображений) по найденным изображениям.
В качестве примера использования операторного метода определим ток через катушку индуктивности в цепи на рис. 1.
С учетом нулевого начального условия операторное изображение этого тока
.
Для нахождения оригинала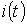 
воспользуемся формулой разложения при нулевом корне
 ,
| (1) |
где 
, 
.
Корень уравнения 
.
Тогда
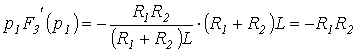
и
.
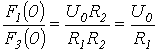Подставляя найденные значения слагаемых формулы разложения в (1), получим
.
Воспользовавшись предельными соотношениями, определим 
и 
:
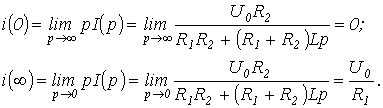
Формулы включения
Формулу разложения можно использовать для расчета переходных процессов при нулевых и ненулевых начальных условиях. Если начальные условия нулевые, то при подключении цепи к источнику постоянного, экспоненциального или синусоидального напряжения для расчета переходных процессов удобно использовать формулы включения, вытекающие из формулы разложения.
- Формула включения на экспоненциальное напряжение
 ,
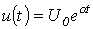
| (2) |
где 
- входное операторное сопротивление двухполюсника при определении тока в ветви с ключом (при расчете тока в произвольной ветви это операторное сопротивление, определяющее ток в ней по закону Ома);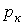 
- к-й корень уравнения 
.
- Формула включения на постоянное напряжение
(вытекает из (2) при 
)
.
- Формула включения на синусоидальное напряжение
(формально вытекает из (2) при 
и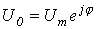 
)
.
В качестве примера использования формулы включения рассчитаем ток в цепи на рис. 2, если в момент времени t=0 она подсоединяется к источнику с напряжением 
; 
; 
.
В соответствии с заданной формой напряжения источника для решения следует воспользоваться формулой (2). В ней 
. Тогда корень уравнения 
. Производная 
и 
.
В результате
.
Сведение расчета переходного процесса к расчету
с нулевыми начальными условиями
Используя принцип наложения, расчет цепи с ненулевыми начальными условиями можно свести к расчету схемы с нулевыми начальными условиями. Последнюю цепь, содержащую пассивные элементы, можно затем с помощью преобразований последовательно-параллельных соединений и треугольника в звезду и наоборот свести к виду, позволяющему определить искомый ток по закону Ома с использованием формул включения.
|
|
|
Методику сведения цепи к нулевым начальным условиям иллюстрирует рис. 3, на котором исходная схема на рис. 3,а заменяется эквивалентной ей схемой на рис. 3,б, где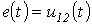 
. Последняя в соответствии с принципом наложения раскладывается на две схемы; при этом в схеме на рис. 3,в составляющая 
общего тока 
равна нулю. Таким образом, полный ток равен составляющей тока 
в цепи на рис. 3,г, где исходный активный двухполюсник АД заменен пассивным ПД, т.е. схема сведена к нулевым начальным условиям.
Следует отметить, что если определяется ток в ветви с ключом, то достаточно рассчитать схему на рис. 3,г. При расчете тока в какой-либо другой ветви АД в соответствии с вышесказанным он будет складываться из тока в этой ветви до коммутации и тока в ней, определяемого подключением ЭДС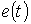 
к пассивному двухполюснику.
Аналогично можно показать, что отключение ветви, не содержащей индуктивных элементов, при расчете можно имитировать включением в нее источника тока, величина которого равна току в ветви до коммутации, и действующему навстречу ему.
Переходная проводимость
При рассмотрении метода наложения было показано, что ток в любой ветви схемы может быть представлен в виде
,
где 
- собственная (к=m) или взаимная 
проводимость.
Это соотношение, трансформированное в уравнение
 ,
| (3) |
будет иметь силу и в переходном режиме, т.е. когда замыкание ключа в m-й ветви подключает к цепи находящийся в этой ветви источник постоянного напряжения 
. При этом 
является функцией времени и называется переходной проводимостью.
В соответствии с (3) переходная проводимость численно равна току в ветви при подключении цепи к постоянному напряжению 
.
|
|
|
