Определение закона распределения вероятности результатов измерений.

Определив оценки основных начальных и центральных моментов и показателей формы, можно предварительно определить характер кривой плотности распределения вероятности.

Так, например, если оценка асимметрии не близка к нулю (не выполняется неравенство │А│ ≤1,5 ), то кривую плотности распределения вероятности нельзя считать симметричной, при этом если А<0, то более крутая часть кривой находится справа. Степень несимметричности кривой распределения плотности вероятности можно оценивать и по тому, каким образом массив экспериментальных данных нарывается интервалом, рассчитанным по формуле (14): если значительная часть левой или правой половины этого интервала накрывает участок значений, экспериментальные данные в котором отсутствуют, то указывает на наличие существенной несимметричности кривой распределения вероятности. И еще одним показателем несимметричности кривой может быть отличие среднего арифметического от медианы. Чем больше они отличаются друг от друга, тем большая несимметричность кривой распределения вероятности.

По величине оценки эксцесса можно оценить степень заостренности кривой распределения плотности вероятности. Если , то можно считать, что закон распределения плотности вероятности близок к нормальному. При кривая имеет более узкую, острую и высокую вершину, чем у нормального закона, при – более широкую, плоскую и низкую.

Наличие моды (или нескольких мод) может быть оценено по анализу частот тех или иных значений экспериментальных данных. Если экспериментальные данные имеют тенденцию группироваться в какой-либо области значений (или областях значений), то можно говорить о возможности наличия моды (или нескольких мод). Однако следует учитывать, что без построения гистограммы оценить значение той или иной моды невозможно.

Для уточнения формы ЗРВ построим гистограмму.

Гистограмма представляет собой ступенчатый график, состоящий из прямоугольников, у которых основаниями служат частные интервалы на оси абсцисс, а площади равны частотам (или частостям) вариантов, попадающих в эти интервалы.

Если число интервалов, на которые разбивается вся совокупность экспериментальных данных, будет велико, а интервалы соответственно будут малыми, то гистограмма будет отличаться от плавной кривой своей изрезанностью, многими всплесками и впадинами, а некоторые интервалы могут быть пустыми. Такие гистограммы иногда называют гребенчатыми. Если число интервалов будет мало, то могут быть потеряны характерные особенности действительного закона распределения вероятности. Так, например, если сделать один интервал, равный размаху экспериментальных данных, то любое распределение вероятности будет сведено к равномерному закону.

Значение числа интервалов находится между минимальными и максимальными числами, которые могут быть определены по формулам:

m_min=0,55n^0,4=0,55*39^0,4≈3;

m_max=1,25n^0,4=1,25*39^0,4≈5; (13)

где n – число отсчетов.

Принимаем одно значение числа интервалов, для построения гистограмм, а именно 5 интервалов.

Определим длины интервалов 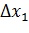по формуле:

,

где m – число интервалов гистограммы.

Устанавливаем граничные значения интервалов. Наименьшее граничное значение для первого интервала будет равно х_min. Вторую границу интервала найдем, прибавляя длину интервала х.

Составим таблицу для подсчета частот соответствующих интервалов:

 

Таблица 3 – подсчет частот интервалов.

№ интервала	Границы интервала	Середина интервала	Подсчет частот	Частота, N
	0,443…0,461	0,452		6,968
	0,461…0,480	0,471		15,329
	0,480…0,498	0,489		5,574
	0,498…0,517	0,508		12,542
	0,517…0,535	0,526		13,935

 

Строим гистограмму распределения, нанося по оси абсцисс границы интервалов, а по оси ординат – шкалу частот. Для каждого класса строим прямоугольник с основанием, равным ширине интервала, и с высотой, соответствующей частоте попадания данных в этот интервал или частости (относительно количеству отсчетов, приходящихся на данный интервал), определяемой по отношению:

N= , (14)

где N_i – частота (количество отсчетов, попавших в данный интервал);

n – количество отсчетов в исходном массиве;

– длина интервала.

Таким образом, в гистограмме площадь прямоугольника равна вероятности попадания отсчета в интервал, которым является основание прямоугольника.

 

Рисунок 1- гистограмма, построенная по данным таблицы 3 (m=5).

 

По внешнему виду гистограммы на рисунке 1 можно считать, что результат измерения подчиняется равномерному закону распределения вероятности.

 

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: