 |
Использование критериев согласия при идентификации формы распределения результатов измерения
|
|
|
|
В качестве способа оценки близости распределения выборки экспериментальных данных к принятой аналитической модели закона распределения обычно рекомендуется использование так называемых критериев согласия.
Критерии согласия позволяют оценить вероятность того, что полученная выборка не противоречит сделанному предположению о виде закона распределения рассматриваемой случайной величины.
Проверим гипотезу о принадлежности результатов измерения к равномерному распределению по критерию К. Пирсона.
В критерии согласия К. Пирсона (критерий χ2) за меру расхождения принимается величина χ2 , опытное (расчетное) значение χ2q которой определяется формулой
χ2q = 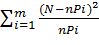 , (15)
, (15)
где m – число сравниваемых частот (число интервалов, на которые разбиты все результаты измерений величины х).
Ni - частота (количество отсчетов, попавших в i- тый интервал);
n – количество отсчетов в исходном массиве результатов измерений;
Pi – вероятность попадания случайной величины х в i- тый интервал.
Плотность нормированного распределения p(ti) (графа 5) в зависимости от значения аргумента может быть определена по таблице приложения 8.
Таблица 5 - Расчет критерия Пирсона
| i | Середина интервала, х | Частота, Ni | Плотность в серединах интервалов p(xi)=p(ti)/Sx | Теоретическая частота
nPi=n  xp(xi) xp(xi)
| Критерий пирсона

|
| 0,452 | 10,8696 | 7,8 | 1,005 | ||
| 0,471 | 10,8696 | 7,8 | 1,313 | ||
| 0,489 | 10,8696 | 7,8 | 1,851 | ||
| 0,508 | 10,8696 | 7,8 | 0,185 | ||
| 0,526 | 10,8696 | 7,8 | 0,621 | ||
| ∑=4,975 |
Выбираем по приложению 3 значение  , которое в зависимости от числа степеней свободы k=m-3=5-3=2 (m=5, где m–число столбцов гистограммы) и уровня доверительной вероятности (проверку по критериям согласия проводят при q = 0,01) Р=0,99 равно 9,210, следовательно можно принять гипотезу о том, что результат измерения подчиняется равномерному закону распределения вероятности.
, которое в зависимости от числа степеней свободы k=m-3=5-3=2 (m=5, где m–число столбцов гистограммы) и уровня доверительной вероятности (проверку по критериям согласия проводят при q = 0,01) Р=0,99 равно 9,210, следовательно можно принять гипотезу о том, что результат измерения подчиняется равномерному закону распределения вероятности.
|
|
|
Определение доверительных границ случайной погрешности результата измерений
Необходимо определить доверительные границы случайной погрешности измерений при вероятности Р = 0,99.
После обработки массива результатов измерений были получены:
- среднее арифметическое значение результата измерений:
 = 0,491
= 0,491
- оценка СКО среднего арифметического значения:

Так как было установлено, что ЗРВ равномерный, то параметр tp вычислялся ранее по формуле (11).
Р = 0,99 (n=39), tp = 2,43
Граничные значения случайной погрешности измерения составят:
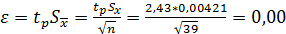 16 (м) (16)
16 (м) (16)
 (17)
(17)

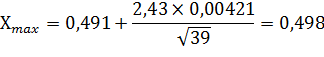

Определение доверительных границ неисключенной систематической погрешности результата измерения.
Неисключенной систематическая погрешность результата образуется из составляющих, в качестве которых могут быть неисключенные систематические погрешности:
-метода;
-средств измерений;
-вызванные другими источниками.
Неисключенные систематические погрешности принято рассматривать как случайные с равномерным симметричным законом распределения плотности вероятности и определять каждую границами ±θ i. Причем в качестве границы ±θ i принимаем пределы допускаемых основных и дополнительных погрешностей средств измерений.
На основе изучения метрологических характеристик датчика уровня топлива установлено, что он имеет следующие относительные приведенные погрешности:
- погрешность измерения температуры - + 20С;
- погрешность, вызванная изменением температур в диапазоне от -600С до +600С - + 0,8%;
- погрешность, вызванная изменением температур в диапазоне от -600С до +800С - + 1%;
Через формулу относительной приведенной погрешности выразим абсолютную погрешность, которая будет выражена в единицах измеряемой величины, а именно в метрах.
|
|
|
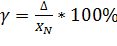 , (18)
, (18)
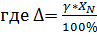 ,
,
XN=0,491; 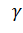 1=2;
1=2; 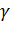 2=0,8;
2=0,8; 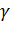 3=1.
3=1.
Подставив все данные в формулу получим, что  1=0,0098 (м),
1=0,0098 (м),  2=0,0039 (м),
2=0,0039 (м),  3=0,0049 (м).
3=0,0049 (м).
После вычисления отношения l =0,0049/0,0039=1,25 найдем коэффициент k который будет равен - 1,37.
Значение общей границы погрешности  :
:
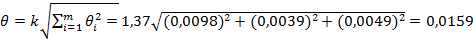 (19)
(19)
|
|
|


