Практическое использование

1 начала термодинамики

 

Характер реакции:

Критерий:

 

Энергетическая ценность

пищевых продуктов DН⁰

Глава 3 Второе начало термодинамики.

 

3.1. Самопроизвольные процессы

Понятие «второе начало термодинамики» было введено в 1850г. Ру­дольфом Клаузиусом в связи с необходимостью решения вопросов, на ко­торые не давало ответ первое начало термодинамики. Эти вопросы воз­никли из анализа работы тепловых двигателей, в которых необходимо было превратить теп­лоту в меха­ническую энергию (максимальную ра­боту).

Согласно закону сохранения энергии – первому началу термодинамики – энергия должна превращаться из одного вида в другой в эквивалентных коли­чествах. Однако опыт показывает, что в то время как все формы энергии (меха­ническая, электрическая, лучистая, химическая) могут полностью превращаться

в тепловую энергию, тепло нельзя полностью превратить в энергию меха­ническую, электрическую, химическую и т.д. Всегда остаётся часть тепла, которая не может превратиться в другие виды энергии(Уильям Томсон)

Приведена одна из нескольких формулировок второго начала термодинамики.

Проиллюстрируем на примере работы двигателя внутреннего сгорания. В цилиндр впры­скивается топливная смесь, которая сжимается поршнем до вы­сокого давле­ния, после чего она воспламеняется. При сгора­нии смеси выде­ля­ется зна­чительное количество теплоты в виде раскален­ных и расширяю­щихся продук­тов, давление которых толкает поршень. В идеальном случае вся эта теп­лота потратилась бы на соверше­ние работы по движению поршня вверх и вниз. На самом деле такого не происходит. Во-первых, стенки цилиндра всегда на­грева­ются в ре­зультате горения рабочей смеси. Во-вто­рых, часть работы неиз­бежно ухо­дит на преодоление силы трения. В-третьих, цилиндру нужно вер­нуться к исходной точке сжатия. В ходе всех перечислен­ных процессов часть вы­делившегося тепла никак не связано с превраще­нием в «полезную» ра­боту поршня, т.е. оно тра­тится «вхолостую.

Ещё один пример. Согласно первому началу термодинамики возможны лю­бые процессы, идущие без нарушения закона сохранения энергии. На­пример, тепло может самопроизвольно переходит как от горячего тела к холодному, так и от холодного к горячему (сколько одно тело отдаст те­пла, столько получит другое). Однако из жизненного опыта мы знаем, что

самопроизвольно тепло передается только от горячего тела к холод­ному, а не наоборот.

Эта формулировка второго начала термодинамики принадлежит Р. Клау­зиусу.

Таким образом, приведённые примеры показывают, что второе начало тер­модинамики изучает возможность превращения энергии из одного вида в дру­гой, т.е. возможность осуществления самопроизвольных процессов и глу­бину их протекания. Для химических реакций второе начало термодинамики изучает возможность ее самопроиз­вольного про­текания.

Самопроизвольными называют процессы, протекающие без постоянного подвода энергии извне

Из двух взаимообратных процессов, если прямой протекает самопроиз­вольно, то обратный самопроизвольно протекать не может; для него требу­ется затрата энергии извне. Т.о. самопроизвольные процессы необратимы. Второе начало термодинамики утверждает, что природные и технологические про­цессы самопроизвольно могут протекать только в одном направлении, стремясь к состоянию равновесия. Приме­рами самопроизвольных процессов являются:

а) горение топлива, в) испарение,

б) расширение газа, г) растворение и др.

Каков же критерий само­произвольного протекания процессов и химиче­ских ре­акций, что является их движущей силой? На первый взгляд ка­жется, что само­произвольно про­текают процессы, идущие с выделением большого количества тепла, т.е. экзотермические, ΔН < 0 (пример а)). Од­нако другие примеры пока­зывают, что самопроизвольные процессы могут протекать и без тепловых эф­фектов ΔН = 0 (пример б)) или даже с погло­щением тепла, ΔН > 0 (пример в)). В поисках критерия самопроизвольно­сти протекания процесса появилась необхо­димость введения новой термо­динамической функции, называемой энтропией.

3.2. Энтропия

Энтропия (от греч en – «в» и tropia – «превращение», т.е. превращение в сис­теме) обозначается символом S, Дж/моль∙К

Энтропия – термодинамическая функция, характеризующая неупо­рядо­ченность расположения частиц в системе в результате их теплового движения, это мера беспорядка в системе.

Энтропия является характеристикой макросистем, состоящих из большого числа микро­час­тиц. Её физический смысл был раскрыт Людвигом Больцманом в 70-е годы Х1Х века.

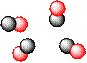
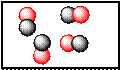
Например, пусть в замкну­том сосуде помещены 4 молекулы двухатом­ного газа при постоян­ных условиях. Молекулы будут принимать в про­странстве различные положе­ния, двигаться в разные стороны с раз­личной ско­ростью.

 

 

Приведённые рисунки отражают некоторые возможные варианты распо­ло­жения молекул в сосуде. При этом макросостояние системы будет оставаться неизменным и характеризоваться разными микро­состояниями, где молекулы отличаются пространственным расположе­нием, скоростью передвижения и т.д. Совокупность этих микросостояний стали называть «неупорядочен­ностью» или «беспо­рядком» в системе и характеризовать величиной энтропии.

Число таких микросостояний Больцман назвал термодинамической ве­роят­ностью (W). Поскольку вероятность – достаточно большая величина, по­этому более удобно выра­жать ее через натуральный логарифм, отнесенный к 1 частице веще­ства (атом, молекула).

S = k•lnW (7)

 

k – постоянная Больцмана

Следовательно, энтропия – функция состояния системы, характеризующая неупоря­до­ченность расположения её частей. Чем больше неупорядоченность, тем значе­ние энтро­пии выше. Эта формула была приведена вместо эпита­фии на па­мятнике Больцману ввиду её огромной значимости для науки.

Факторы, влияющие на значение энтропии вещества

1. Агрегатное состояние. Самое низкое значение энтропии характерно для твер­дого состояния, в котором порядок расположения частиц наиболь­ший. При переходе из твердого состояния в жидкое значительно увеличива­ется неупоря­доченность и соответственно энтропия вещества. Наи­большее значение энтро­пии достигается в газообразном состоянии

 

Н₂О (лёд) Н₂О (ж) Н₂О (пар)

S°₂₉₈ Дж/моль∙К 39 70 189

Также рас­тет энтропия при переходе вещества из кристаллического в аморфное состояние. Например, S°₂₉₈ алмаза 2,34 Дж/моль∙К, а S°₂₉₈ гра­фита 5,7 Дж/моль∙К.

2.Увели­чение числа атомов в молекуле и усложнение молекулы приво­дит к увеличе­нию энтропии. Например, S°₂₉₈ (О) = 161, S°₂₉₈(О₂) = 205,

S°₂₉₈(О₃) = 238,8 Дж/моль∙К.

3. С увеличением температуры хаотичность движения частиц, а сле­до­ва­тельно, и энтропия системы, возрастает.

4. Как правило, при повышении давления энтропия газов уменьшается.

5. Энтропия возрастает в реакциях, в ходе которых образуются газооб­раз­ные и жидкие вещества из твёрдых, увеличивается число молекул. Если же в ходе реакции образуется сложное вещество, содержащее большее число атомов, то это приводит к упорядочению системы и, следовательно, к уменьшению энтро­пии. Поэтому можно оценить знак изменения энтро­пии в реакции, не прибегая к расчётам, как например, в реакции получения кислорода при разложении KClO₃

2KClO₃ (ТВ) 2KCl (ТВ) + 3O₂ (Г) ΔS > 0

 

Чтобы значения энтропии веществ были сопоставимы, их относят к стандарт­ным условиям: Т = 298К (25°С), Р = 101325 Па и v (в-ва) = 1 моль. Эн­тропия веще­ства в этих условиях обозначается S°₂₉₈ и называется абсо­лютной или стандартной энтропией. Обратите внимание, что в обозначе­нии стандарт­ной энтропии отсутствует знак Δ, в отличие от стандартной энтальпии образо­вания вещества (ΔН°₂₉₈). Объясняется это тем, что для изменения энталь­пии вещества не существует точки начала её отсчета и приходится пользоваться только лишь измене­ниями энтальпии. Для энтро­пии такая точка начала отсчёта существует – это точка абсолютного нуля.

 

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: