Главная | Обратная связь | Поможем написать вашу работу!
 МегаЛекции

Контрольная работа по разделу«Аналитическая геометрия».




Зачет по геометрии(4 семестр).

1. Геометрические векторы. Линейные операции над векторами и их свойства.
2. Проекция вектора на ось. Коллинеарные и компланарные векторы. Базис векторов на прямой, плоскости и в пространстве. Координаты вектора. 
3. Скалярное произведение векторов, его основные свойства, координатное выражение.
4. Векторное произведение векторов, его основные свойства, геометрический и физический смысл.
5. Смешанное произведение векторов, его основные свойства, и геометрический смысл.
6. Координатное выражение векторных и смешанных произведений.
7. Аффинные и прямоугольные системы координат на плоскости и в пространстве. Формулы преобразования систем координат.
8. Основные задачи, решаемые в аффинной системе координат. Деление отрезка в данном отношении.
9. Основные задачи, решаемые в прямоугольной системе координат: измерение длин, углов, площадей и объемов.
10. Полярная, цилиндрическая и сферическая системы координат.
11. Множества. Метод координат на плоскости. Линия как множество точек. Уравнение линии на плоскости. Построение линии по ее уравнению. Некоторые элементарные задачи. Две основные задачи аналитической геометрии. Алгебраические линии. Окружность.
12. Различные уравнения прямой линии на плоскости. Уравнение прямой, проходящей через данную точку в данном направлении. Уравнение прямой, проходящей через две данные точки. Уравнение прямой в “отрезках”. Каноническое уравнение, общее уравнение, уравнение прямой с угловым коэффициентом.
13. Взаимное расположение прямых на плоскости. Точка пересечения двух прямых. Угол между прямыми линиями. Расстояние от точки до прямой. Полуплоскость.
14. Эллипс. Каноническое уравнение эллипса. Свойства эллипса. Эллипс как равномерная деформация окружности.
15. Гипербола. Каноническое уравнение гиперболы.. Свойства гиперболы.. Асимптоты гиперболы. График обратной пропорциональности.
16. Парабола. Каноническое уравнение параболы. График квадратного трехчлена.
17. Директориальные (фокальные) свойства эллипса, гиперболы и параболы. Их уравнения в полярной системе координат. Конические сечения.
18. Два способа приведения кривой второго порядка к каноническому виду. Девять видов кривых второго порядка
19. Плоскость в пространстве и ее различные уравнения.
20. Взаимное расположение двух и трех плоскостей в пространстве. Угол между плоскостями. Расстояние от точки до плоскости.
21. Прямая линия в пространстве и их различные уравнения.
22. Взаимные расположения прямых и плоскостей в пространстве. Полупространство.
23. Углы между прямыми линиями в пространстве. Расстояние между прямыми линиями.
24. Поверхности вращения.
25. Цилиндрические и конические поверхности и их уравнения.
26. Эллипсоид. Однополостный гиперболоид Двуполостный гиперболоид и его прямолинейные образующие.
27. Эллиптический параболоид. Гиперболический параболоид и его прямолинейные образующие.
28. Аксиомы элементарной геометрии. Основные понятия и следствия системы аксиом.
29. Начала элементарной геометрии. Треугольники. Равенство фигур.
30. Параллельность.
31. Подобие фигур. Признаки подобия. Теорема Фалеса.
32. Метрические соотношения в треугольнике.
33. Четыре замечательные точки в треугольнике.
34. Теоремы синусов и косинусов.
35. Периметры, углы и площади геометрических фигур. Формула Герона.
36. Окружность и круг. Основные метрические соотношения в окружности.
37. Длина окружности, площадь круга и его частей.
38. Начала стереометрии. Аксиомы. Основные определения,
39. Свойства и признаки параллельности, перпендикулярности, теорема о трех перпендикулярах
40. Основные типы выпуклых тел в элементарной геометрии.
41. Объемы выпуклых тел и их измерение
42. Объем пирамиды и объем усеченной пирамиды.
43. Конус, усеченный конус, их площади поверхностей и объемы.
44. Сфера и ее площади поверхности.
45. Объем шара и его частей.
46. Выпуклые фигуры и их свойства.
47. Многогранные углы и сферические треугольники
48. Сумма углов и площадь сферического треугольника.
49. Тригонометрия трехгранных углов и сферических треугольников.
50. Основные задачи. Этапы решения задач на построение.
51. Основные методы решения задач на построение.
52. Теорема о разрешимости задачи на построение.

Самостоятельная работа заключается в изучении теоретического материала и решении задач. Составляет не менее 100 часов.

На зачете необходимо предъявить материалы, которые показывают, что студент занимался самостоятельной работой по геометрии во вне сессионное время. Прорешать предложенные задачи и разобраться в теоретических вопросах.

Теоретический материал изучать по предложенной литературе и по школьным учебником, рекомендованным ниже.

Контрольная работа по разделу«Аналитическая геометрия».

Примерный вариант контрольной работы

 

  1. Пусть в треугольнике ABC  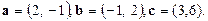Изобразить векторы a, b, c и разложить вектор с по векторам a и b.
  2. Пусть a =(2,2,2), b =(1,-1,2), c =(-1,3,4). Вычислить |2 a -3 b |, cosÐ(a, 2 a -3 b), ab, a ´ b, abc.
  3. Даны вершины A(2,-2), B(8, -8), C(5, 7) ан треугольника АВС. Найти площадь треугольника ABC. Точку пересечения медиан. Уравнение медиан AM. Уравнение высоты AH. Расстояние от вершины A до стороны BC. Тангенс угла A.
  4. Даны вершины A(2,-2,1), B(8, -8,2), C(5, 7, 3), D(-5,-7,-8) пирамиды АВСD. Найти объем пирамиды ABCD. Найти косинус двухгранногоугола при ребре AB. Уравнение плоскости ABC. Уравнение высоты DH. Расстояние от вершины D до плоскости ABC. Найти расстояние от прямой AB до прямой C3.
  5. Найти уравнения эллипса, если b=5, e = 0,4 и гиперболы, если b=5, e = 3. Найти их фокусы и директрисы. Построить эллипс и гиперболу, их фокусы и директрисы.

 

Примерный вариант контрольной работы по элементарной математике

1. Около круга радиуса 2 см описана равнобочная трапеция с площадью 20 см2. Найдите длины сторон трапеции.

2. Построить треугольник по данному основанию, боковой стороне и высоте, опущенной на основание.

3. Построить треугольник по двум углам и медиане.

4. Построить параллелограмм, зная одну из сторон, опущенную на эту сторону высоту и одну из диагоналей.

5. Построить треугольник по основанию, боковой стороне и медиане, проведенной к основанию.

6. Построить окружность данного радиуса, проходящую через две данные точки.

7. Найти объем конуса, вписанного в правильную треугольную пирамиду с боковым ребро l и плоским углом a при вершине.
Поделиться:





Воспользуйтесь поиском по сайту:



©2015 - 2025 megalektsii.ru Все авторские права принадлежат авторам лекционных материалов. Обратная связь с нами...