Расчет зубчатой цилиндрической передачи

 

По заданию на курсовую работу необходимо спроектировать зубчатую цилиндрическую прямозубую передачу редуктора для привода общего назначения.

В настоящее время при индивидуальном и мелкосерийном производстве цилиндрические прямозубые колеса закрытых передач изготавливают из сталей 40, 45, 40Х, а для упрочнения материала проводят термическую обработку: нормализацию, улучшение, закалку [3]. Твердость материала колес меньше или равна 350 НВ (по шкале Бринелля), что обеспечивает чистовое нарезание зубьев после термообработки, высокую точность изготовления и хорошую прирабатываемость зубьев. Меньшее колесо в паре называют шестерней (при расчетах её параметрам присваивается индекс 1), а колесу присваивается индекс – 2. Для равномерного изнашивания зубьев и лучшей их прирабатываемости твердость шестерни НВ₁ назначается больше твердости колеса НВ₂ на 20…50 единиц [3].

При работе передачи зубья испытывают контактные s_H и изгибные s_F напряжения. Расчет закрытой цилиндрической прямозубой передачи в курсовой работе проводится только по контактным напряжениям, так как большая статистика расчетов этих передач при средних режимах нагружения и длительном режиме эксплуатации показывает, что при обеспечении контактной прочности изгибная прочность выполняется. При условиях работы передачи, отличных от заданий на курсовую работу, можно воспользоваться источником [4]. В качестве исходных данных для расчета зубчатой передачи в курсовой работе можно принять материалы и механические характеристики шестерни и колеса, приведенные в таблице 5 [2].

Таблица 5 – Материалы колес и их механические характеристики

Характеристики	Шестерня	Колесо
Марка стали	Сталь 40Х ГОСТ 4543-71	Сталь 45 ГОСТ1050-88
Метод получения заготовки	Поковка	Поковка
Термическая обработка	Улучшение	Улучшение
Интервал твердости, НВ	269…302	235…262
Средняя твердость, НВср	285,5	248,5
Предел текучести, sТ, Мпа
Предел прочности, sВ, Мпа
Допускаемое контактное напряжение: шестерни – [sН1], колеса – [ sН2], МПа
Максимально допускаемое напряжение при перегрузках [ sН мах], МПа

 

Средняя твердость поверхности зуба по Бринеллю

. (21)

Допускаемые контактные напряжения при номинальной нагрузке

[ s_Н ] и при перегрузках [ s_{Н мах} ] рассчитаны по [4].

Дальнейшую методику расчета зубчатой цилиндрической прямозубой передачи проследим на рассматриваемом примере.

 

Пример расчета

 

 

Главный геометрический параметр цилиндрической зубчатой передачи – межосевое расстояние (рисунок 2). Предварительное его значе -

 

 

Рисунок 2 – Геометрические параметры цилиндрической

зубчатой передачи

 

Рисунок 3 – Схема сил в зацеплении цилиндрических прямозубых

зубчатых колёс

ние рассчитывается из условия контактной выносливости рабочих поверхностей зубьев [3, с. 61] по формуле

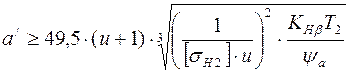, (22)

где Т ₂ – вращающий момент на валу колеса (3-й вал привода), Н×мм;

K_Hb – коэффициент концентрации нагрузки. Для прирабатывающихся колес K_Hb = 1 [3, c. 61];

y_а – коэффициент ширины колеса. Для одноступенчатого цилиндрического редуктора при симметричном расположении колес относительно опор y_а = 0,4 или 0,5 [4];

u – передаточное число зубчатой передачи, u = u_ЗП;

[ s_Н2 ] – допускаемое контактное напряжение для материала колеса, так как колесо имеет более низкую прочность по сравнению с шестерней.

Рассчитаем предварительное значение межосевого расстояния

.

Значение округляют до ближайшего большего значения по единому ряду главных параметров редуктора [4]: 25, 28, 30, 32, 36, 40, 45, 50, 56, 63, 71, 80, 90, 100, 112, 125, 140, 160, 180, 200, 224, 250, 280, 315, 355, 400. При небольшом превышении над стандартным значением (до 3…5%) допускается выбирать меньшее стандартное значение межосевого расстояния. Поэтому принимаем = 112мм.

Предварительная ширина колеса и шестерни равна

, (23)

(24)

Значения b^/ ₁ и b^/ ₂ округляют до ближайших стандартных значений из ряда главных параметров (см. выше): b₁ = 50 мм; b₂ = 45 мм.

Модуль зубчатых колес выбирают в следующем интервале:

m^/ = (0,01…0,02) × а = (0,01…0,02) ×112 = 1,12…2,24 мм. (25)

Для силовых передач значение модуля m должно быть больше или равно 1,0 мм и соответствовать по ГОСТ 9565-80 ряду (мм): 1,0; 1,25; 1,5; 1,75; 2,0; 2,25; 2,5; 2,75; 3,0; 3,5; 4,0; 4,5; 5,0; 5,5; 6,0. Жирным шрифтом выделены предпочтительные модули.

Выбираем модуль m = 2,0 мм.

Определим числа зубьев колес. Предварительное суммарное число зубьев колес вычисляют из соотношения

 

(26)

Предварительное значение суммарного числа зубьев желательно получить сразу целым числом, чтобы не вводить коррекцию (смещение исходного контура) зубчатых колес. Это можно обеспечить подбором модуля m в интервале по формуле (25).

Предварительное значение числа зубьев шестерни находят из соотношения

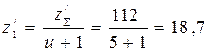. (27)

Полученные значения z^/_å и z^/₁ округляют до ближайшего целого значения z_å = 112 и z₁ = 19. Причем для обеспечения неподрезания ножки зуба прямозубой шестерни необходимо, чтобы значение z₁ было больше или равно 17. После этого вычисляют число зубьев колеса

. (28)

Таким образом, Z₂ = 93 и Z₁ = 19.

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: