 |
Оптимизационные методы переменной метрики
|
|
|
|
Оглавление
Введение
Основные понятия
Оптимизационные методы переменной метрики
Метод Бройдена (Δη (k) имеет ранг 1)
Метод Дэвидона - Флетчера - Пауэлла
Алгоритмы Пирсона
Метод Флетчера
Инструкция пользователя
Заключение
Список литературы
Введение
Когда говорят о задачах математического программирования (планирования), то имеют в виду класс задач оптимизации, возникших ближе к концу Второй мировой войны в связи с попытками повысить эффективность промышленных, транспортных, военных систем за счет улучшений в работе координирующих и управляющих органов. Несмотря на разнообразие смыслового содержания таких задач, все они с формальной точки зрения сводятся к одной общей постановке: найти значения переменных, доставляющие максимум (минимум) некоторой скалярной функции при некоторых условиях. Для каждой задачи строится определенная математическая модель и в зависимости от нее происходит выбор соответствующего алгоритма (метода) оптимизации.
Объектом исследования данной курсовой работы стали численные оптимизационные методы переменной метрики.
Цель работы: Изучение теории численной оптимизации переменной метрики и создание программы, демонстрирующей работу некоторых методов данного типа оптимизации.
Для достижения поставленной цели были решены следующие задачи:
. Изучение теории численной оптимизации переменной метрики;
2. Написание модуля, включающего реализацию некоторых методов.
3. Реализация программы, демонстрирующей работу модуля.
Основные понятия
Исследование операций (ИО) - дисциплина, зародившаяся в 40-е - 50-е года 20 столетия, занимающаяся разработкой и применением методов нахождения оптимальных решений на основе математического моделирования, статистического моделирования и различных эвристических подходов в различных областях человеческой деятельности.
|
|
|
Часто возникает необходимость решения задач, проблема которых состоит в оптимизации расходов сырья, денежных расходов и т.п. Для таких задач, как правило, строится математическая модель, благодаря которой происходит выбор метода оптимизации, состоящего из определенных операций (сам метод тоже является операцией).
Операцией называется всякое мероприятие (система действий), объединенное единым замыслом и направленное к достижению какой-то цели. Операция есть всегда управляемое мероприятие, то есть от лица, принимающего решение (ЛПР) зависит, каким способом выбрать некоторые параметры, характеризующие ее организацию. «Организация» в данном случае понимается в широком смысле слова, включая набор технических средств, применяемых в операции.
Всякий определенный выбор зависящих от ЛПР параметров называется решением. Решение может быть как удачным, так и неудачным. Оптимальным называется решение, которое по тем или иным признакам предпочтительнее других.
Математическое моделирование - замена реального изучаемого объекта объектом заменителем - математической моделью - и, в дальнейшем - изучение модели с помощью реализуемых на персональном компьютере вычислительно-логических алгоритмов. Соответственно, математическая модель - это модель, которая, с помощью некоторых математических законов, описывает основные интересующие исследователя стороны исследуемого объекта.
Основным делением по классам задач математического моделирования является деление по характеру взаимосвязи между переменными:
* Линейные - задачи, в основе которых лежат линейные зависимости;
* Нелинейные - задачи, учитывающие нелинейные связи между факторами.
|
|
|
Задачами нелинейного программирования называются задачи, общая постановка которых следующая:
Найти неотрицательные значения переменных х1, x2,..., xn, удовлетворяющие каким-то ограничениям произвольного вида, например:
(1.1)
и обращающие в максимум (минимум) произвольную нелинейную функцию этих переменных:
(1.2)
Общих способов решения задачи нелинейного программирования не существует; в каждой конкретной задаче способ выбирается в зависимости от вида функции W и накладываемых на элементы решения ограничений.
В отличие от задач линейного программирования, методы решения которых хорошо отлажены, устоялись и не представляют существенных трудностей, задачи нелинейного программирования принадлежат к сложным и трудным вычислительным задачам.
численный переменная метрика модуль
Оптимизационные методы переменной метрики
Класс методов, называемых методами переменной метрики, также называют квазиньютоновскими или градиентными с большим шагом. Эти методы аппроксимируют матрицу Гессе или обратную к ней, но используют для этого только первые производные.
- градиент или вектор столбец из первых частных производных f(x) по x, значения которых берутся в данной точке x.
При использовании методов переменной метрики новый вектор x вычисляется по вектору предыдущего шага с помощью уравнения:
, (1.3)
где матрица 
, которую иногда называют матрицей направлений, представляет собой аппроксимацию 
.
Рассмотрим соотношение, связывающее 
и 
, для случая квадратичной целевой функции (или квадратичной аппроксимации целевой функции)
(1.4а)
Умножая обе части этого уравнения на 
, получаем
(1.4б)
При этом если 
квадратична, то 
, то есть постоянная матрица. Уравнение (1.4б) можно рассматривать как систему n линейных уравнений, содержащих n неизвестных параметров, которые нужно оценить для того, чтобы аппроксимировать или 
при заданных значениях , 
и 
на более ранних этапах поиска. Для решения этих линейных уравнений могут быть использованы различные методы, каждый из которых приводит к различным методам переменной метрики.
В довольно большой группе методов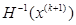 
аппроксимируется с помощью информации, полученной на k -ом шаге:
|
|
|
, (1.5)
где η (x) - матрица, аппроксимирующая 
. 
представляет собой определяемую матрицу, а 
- масштабный множитель, константа, обычно равная единице. Выбор по существу определяет метод переменной метрики. Для обеспечения сходимости 
должна быть положительно определенной и удовлетворять уравнению (1.4б) в том случае, когда она заменяет 
.
На (k + 1) -м шаге мы знаем 
, 
, 
и 
и хотим вычислить 
, так чтобы удовлетворялось соотношение
(1.4в)
Пусть 
. Тогда уравнение
(1.4г)
нужно разрешить относительно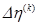 
. Прямой подстановкой результата можно показать, что уравнение (1.4г) имеет следующее решение:
, (1.6)
где y и z - произвольные векторы размерности n x 1. Если для ω = 1 выбирается линейная комбинация двух направлений 
и 
, а именно
,
то используем алгоритм Бройдена; если же берется
, 
,
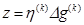то матрицу 
вычисляем с помощью алгоритма Дэвидона - Флетчера - Пауэлла.
Если шаги 
определяются последовательно путем минимизации в направлении 
, то все методы, с помощью которых вычисляют симметрическую матрицу , удовлетворяющую (1.4в), дают направления, являющиеся взаимно сопряженными (в случае квадратичной целевой функции).
Метод Бройдена (Δη ( k ) имеет ранг 1)
Бройден, описывая методы решения систем линейных уравнений, показал, что если 
оказывается симметрической матрицей ранга 1 и должно удовлетворяться соотношение 
, то единственным возможным выбором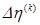 
является
. (1.7)
где
,
.
В простейшем алгоритме этого типа минимизация начинается с выбора начальной точки x (0) и некоторого η (0) > 0; затем последовательно применяются уравнения (1.3), (1.5), (1.7) до тех пор, пока, к примеру, 
. Если для каждого направления поиска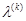 
представляет собой скаляр, минимизирующий 
в этом направлении, то данный метод дает сопряженные направления поиска. Таким образом, при определенных ограничивающих условиях описанному алгоритму обеспечена сходимость. Одной из интересных особенностей методов ранга 1 является то, что 
(или 
) в уравнении (1.3) не обязательно должно быть параметром, минимизирующим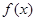 
. Бройден показал, что 
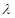может быть произвольным параметром, пока не возникла сингулярность 
или знаменатель в правой части уравнения (1.7) не обратился в нуль. Это свойство позволяет отказаться от одномерного поиска, если есть адекватные альтернативные методы определения .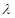
|
|
|
В случае, когда целевая функция не является квадратичной, применение уравнения (1.7) может привести к следующим нежелательным явлениям:
) Матрица может перестать быть положительно определенной. В этом случае необходимо обеспечить положительную определенность матрицы 
.
) Вычисляемая величина 
может стать неограниченной (иногда даже в случае квадратичных функций вследствие ошибок округления).
) Если 
случайно совпадает с направлением предыдущего этапа, матрица 
становится сингулярной или неопределенной.
|
|
|
