Метод Дэвидона - Флетчера - Пауэлла

 

В методе Дэвидона, модифицированном Флетчером и Пауэллом, выбирается матрица , имеющая ранг 2. В данном методе не нужна операция обращения матрицы, как и в методе Бройдена. Матрица направлений  перевычисляется таким образом, чтобы для квадратичной целевой функции в пределе после n шагов она равнялась . Исходная матрица  обычно выбирается в виде единичной матрицы  (но может быть и любой симметрической положительно определенной матрицей), так что исходное направление минимизации - это направление наискорейшего спуска. Оценка элементов  в точке x* (экстремум) тем лучше, чем лучше мы выберем по сравнению с единичной матрицей исходную , однако выбор  определенно предпочтительнее приравнивания элементов  значениям аналитических частных производных или их конечно-разностных приближений в начальной точке . В ходе оптимизации имеет место постепенный переход от градиентного направления к ньютоновскому; при этом используются преимущества каждого из этих двух методов на соответствующем этапе.

Соотношение для 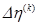 в алгоритме Дэвидона - Флетчера - Пауэлла можно получить путем подстановки

 

 и

 

в уравнение (1.6). Тогда имеем

 

, (1.7а)

 

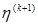где обозначения те же, что и в формуле (1.7). Следует отметить, что вторая и третья матрицы в правой части (1.7а) являются симметрическими, так что если матрица  - симметрическая, то и  будет симметрической.

Рекуррентное соотношение (1.7а) на практике вполне удовлетворительно, если:

)   Ошибка при вычислении  невелика;

)   не становится «плохой».

Роль матрицы  в формуле (1.7а) заключается в обеспечении того, чтобы , тогда как матрица  обеспечивает положительную определенность  на всех этапах и в пределе исключает начальную матрицу . Используем формулу (1.7а) на нескольких этапах, начиная с начальной матрицы:

,

,

.

 

В случае квадратичной функции сумма матриц  должна равняться  при , а сумма матриц  строится так, чтобы она сократилась с матрицей, выбранной в качестве исходной матрицы  (здесь единичной матрицей). Таким образом, метод Дэвидона - Флетчера - Пауэлла отражает до некоторой степени в текущем значении  всю предыдущую информацию.

В большинстве вариаций алгоритма Дэвидона функция минимизируется в каждом выбранном направлении поиска. Для определения минимума  по 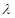 в данном направлении можно применить почти любую эффективную процедуру одномерного поиска. Очень важно, чтобы эта процедура была эффективной, поскольку относительно большая часть всего времени вычисления приходится на одномерный поиск.

Флетчер и Пауэлл предложили выбирать первую длину из последовательности λ* с помощью следующего уравнения

 

,

 

где - наименьшее ожидаемое значение ;

либо положить .

Алгоритмы Пирсона

 

Алгоритм Пирсона №2: Положим в уравнении (1.6) , а . Тогда

,      (1.8)

,

 

где  - произвольная положительно определенная симметрическая матрица. Алгоритм Пирсона №2 обычно приводит к «плохим» матрицам направлений.

Повторение начала алгоритма через каждые n шагов (т.е. приравнивание  к  после каждых n шагов) помогает избежать трудностей, связанных с тем, что матрица направлений перестает быть положительно определенной.

Алгоритм Пирсона №3. Положим в уравнении (1.6) , а .

 

Тогда , (1.9) .

Метод Флетчера

 

,    (1.10)

 

Описываемый алгоритм использует (1.7а). если

 

,

и (1.10), если

.

 

Можно также использовать линейные комбинации уравнений (1.10) и (1.7а). Поскольку матрица , вычисленная с помощью уравнения (1.7а), стремится к нулю с увеличением числа шагов, а , вычисленная с помощью соотношения (1.10), стремится к бесконечности, имеет смысл применять оба типа уравнений.

Эффективной процедуру Флетчера делает скорее не метод вычислений , а кубическая интерполяция при отыскании минимума в данном направлении и ограниченная длина шага. При этом скаляр  выбирается с помощью уравнения , где  - нижняя оценка значений . (Если  оказывается ниже, чем , то имеет место окончание процесса.). Для достижения минимума в направлении поиска используется кубическая интерполяция на интервале между  и . Поскольку для проведения кубической интерполяции не требуется использование всего интервала, содержащего минимум, и результат интерполяции может оказаться неудовлетворительным, если  находится на вогнутой части аппроксимирующего полинома, Флетчер ограничил значение  следующим образом: либо оно должно быть меньше, чем 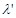, получаемое с помощью кубической интерполяции, либо , где верхний индекс s обозначает номер в последовательности шагов при одномерном поиске.

После каждого шага проводится тест , и если он удовлетворен, то этап считается завершенным. В противном случае продолжается кубическая интерполяция. Окончательно процесс завершается, когда . Во избежание большого влияния ошибок округления или ошибок программ вычисления производных программа останавливается, когда  и 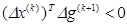 и (или) .

Используя ряд тестовых задач, Флетчер сравнил приведенный выше алгоритм с алгоритмом Дэвидона - Флетчера - Пауэлла и показал, что он столь же эффективен, как и последний. При этом оказалось, что число итераций в каждом направлении поиска уменьшилось, однако для компенсации пришлось увеличить число направлений поиска.

Инструкция пользователя

 

Программа Project1 написана на языке Object Pascal на платформе Delphi 7.0. Данная программа представляет собой реализацию следующих методов: метод Бройдена, метод Дэвидона - Флетчера - Пауэлла, для функции Розенброка f(x, y) = (1 - x)² + 100(y - x²)² → min.

Основной вид программы:

 

Рис. 1.: Программа Project1. Основной вид.

 

Контейнер Method является контейнером выбора соответствующего метода.

·   Broyden’s method - метод Бройдена;

·   Method Davidon-Fletcher-Powell - метод Дэвидона - Флетчера - Пауэлла.

Для того, чтобы выбрать соответствующий метод, наведите курсором мыши на надпись интересующего вас метода и щелкните по этой надписи. В случае успеха рядом с надписью в белый круг будет вписан черный круг.

Контейнер X[0] содержит значения начального вектора. Для того, чтобы ввести определенное значение, в рамках данного контейнера наведите курсором мыши на поле ввода и введите число.

Контейнер N[0] содержит начальную матрицу направлений. Способ ввода аналогичный приведенному выше.

Контейнер Answer отображает ответ в случае успешного окончания соответствующего метода.

Контейнер w содержит значение масштабного множителя. Данный параметр используется только в методе Бройдена.

Контейнер eps содержит в себе значение точности. То есть это точность данного метода.

Кнопка Click. Запуск выбранного метода. Для запуска метода нажмите на кнопку Click.

В случае успешного завершения метода: рядом с надписью «Кол-во итераций:» будет показано число шагов, за которое был найден ответ с заданной точностью; рядом с надписью «Значение функции Розенброка:» будет показано значение функции Розенброка от переменных, найденных с заданной точностью по выбранному методу.

В случае неудачного завершения метода:

 

Рис. 2.: Программа Project1. Метод не нашел минимум функции Розенброка с заданной точностью в 255 шагов.

 

Надпись «Кол-во итераций: Количество итераций превысило число 255» означает, что данный метод не нашел ответ с заданной точностью в 255 шагов.

Строка «NONE» в полях ввода Answer и рядом с надписью «Значение функции Розенброка:» означают, что ответ не был найден, а, следовательно, и значение функции Розенброка тоже неизвестно. Это связано с тем, что в программе стоит ограничение: если метод совершает более 255 шагов, то метод завершает свою работу, так и найдя подходящий ответ.

Если вылезло данное окно, то произошел сбой в работе программы. Для того, чтобы избавиться от данного окна, нажмите кнопку «ОК». В таком случае программа Project1 прекратит свою работу.

 

Рис. 3.: Программа Project1. Сбой в работе программы.

Заключение

 

В ходе курсовой работы был написан модуль, содержащий реализацию методов переменной метрики (метод Бройдена, метод Дэвидона - Флетчера - Пауэлла), а также реализована программа для работы с данным модулем. Были рассмотрены основы теории численной оптимизации переменной метрики.

Список литературы

 

1. Дягтерев Ю.И. Методы оптимизации - М.: Сов. радио, 1980. - 272 с.

2. Вентцель Е.С. Исследование операций. Задачи, принципы, методология. - М.: Наука, 1988. - 208 с.

.   Химмельблау Д. Прикладное нелинейное программирование. - М.: Мир, 1975. - 536 с.

4. Википедия: Свободная Энциклопедия. Статья: Исследование операций. [On-Line]: <http://ru.wikipedia.org/wiki/%D0%98%D1%81%D1%81%D0%BB%D0%B5%D0%B4%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5_%D0%BE%D0%BF%D0%B5%D1%80%D0%B0%D1%86%D0%B8%D0%B9>.

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: