 |
Истечения через отверстия и насадки при переменном напоре (опорожнение сосудов)
|
|
|
|
Рассмотрим случай опорожнения открытого в атмосферу сосуда при постоянно уменьшающемся напоре, при котором течение является неустановившемся (рис.5.10).
Однако если напор, а следовательно, и скорость истечения изменяются медленно, то движение в каждый момент времени можно рассматривать как установившееся, и для решения задачи применить уравнение Бернулли.
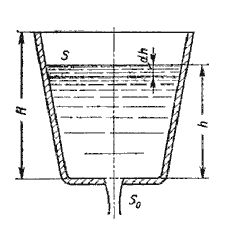
Рис. 5.10. Схема опорожнения резервуара
Обозначим переменную высоту уровня жидкости в сосуде за h, площадь сечения резервуара на этом уровне S, площадь отверстия Sо, и взяв бесконечно малый отрезок времени dt, можно записать следующее уравнение объемов:

где dh - изменение уровня жидкости за время dt.
Отсюда время полного опорожнения сосуда высотой Н

Если будет известен закон изменения площади S по высоте h, то интеграл можно подсчитать. Для призматического сосуда S = const (рис.5.11), следовательно, время его полного опорожнения

Из этого выражения следует, что время полного опорожнения призматического сосуда в два раза больше времени истечения того же объема жидкости при постоянном напоре, равном первоначальному.

| 
|
| Рис. 5.11. Опорожнение призматического резервуара | Рис. 5.12. Опорожнение непризматического резервуара |
Для определения времени истечения жидкости из горизонтального цилиндрического сосуда (цистерны) (рис. 5.12) выразим зависимость переменной площади S от h:

где l - длина цистерны; D - диаметр цистерны.
Тогда время полного опорожнения такой цистерны, т.е. время изменения напора от h1 = D до h2 = 0, получится равным

ТИПЫ НАСАДКОВ
внешние и внутренние. Когда насадок монтируется с внешней стороны резервуара (внешний насадок), то он оказывается более технологичным, что придаёт ему преимущество перед внутренними насадками.
|
|
|
По форме исполнения насадки подразделяются на цилиндрические и конические, а по форме входа в насадок выделяют ещё коноидальные насадки, вход жидкости в которые выполнен по форме струи. Коэффициенты
Отверстие с острой кромкой 0,97
Внешний цилиндрический насадок 0,82
Внутренний цилиндрический насадок 0,71
Конически сходящийся насадок 0,96
Конически расходящийся насадок 0,45
Коноидальный насадок 0,97
Билет 4
2. Взаимодействие жидкости с наклонной твердой
стенкой. Центр давления, его координаты.
3. Истечение жидкости из отверстий. Понятие отверстия в тонкой стенке.
Коэффициент расхода жидкости в отверстии в тонкой стенке.
Математическое выражение, числовое значение.
2) Давление жидкости на плоскую наклонную стенку
Пусть мы имеем резервуар с наклонной правой стенкой, заполненный жидкостью с удельным весом γ. Ширина стенки в направлении, перпендикулярном плоскости чертежа (от читателя), равна b (рис.2.3). Стенка условно показана развернутой относительно оси АВ и заштрихована на рисунке. Построим график изменения избыточного гидростатического давления на стенку АВ.
Так как избыточное гидростатическое давление изменяется по линейному закон P=γgh, то для построения графика, называемого эпюрой давления, достаточно найти давление в двух точках, например А и B.
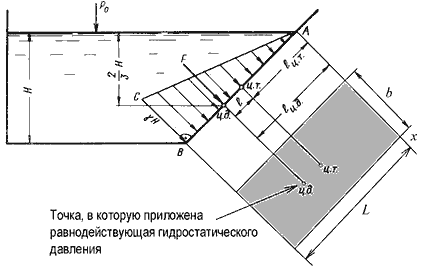
Рис. 2.3. Схема к определению равнодействующей гидростатического давления на плоскую поверхность
Избыточное гидростатическое давление в точке А будет равно
PA = γ h = γ·0 = 0
Соответственно давление в точке В:
PB = γ h = γ H
где H - глубина жидкости в резервуаре.
Согласно первому свойству гидростатического давления, оно всегда направлено по нормали к ограждающей поверхности. Следовательно, гидростатическое давление в точке В, величина которого равна γH, надо направлять перпендикулярно к стенке АВ. Соединив точку А с концом отрезка γH, получим треугольную эпюру распределения давления АВС с прямым углом в точке В. Среднее значение давления будет равно
|
|
|

Если площадь наклонной стенки S=bL, то равнодействующая гидростатического давления равна

где hc = Н/2 - глубина погружения центра тяжести плоской поверхности под уровень жидкости.
Однако точка приложения равнодействующей гидростатического давления ц.д. не всегда будет совпадать с центром тяжести плоской поверхности. Эта точка находится на расстоянии l от центра тяжести и равна отношению момента инерции площадки относительно центральной оси к статическому моменту этой же площадки.

где JАx - момент инерции площади S относительно центральной оси, параллельной Аx.
В частном случае, когда стенка имеет форму прямоугольника размерами bL и одна из его сторон лежит на свободной поверхности с атмосферным давлением, центр давления ц.д. находится на расстоянии b/3 от нижней стороны.
|
|
|


