Понятие о гидравлически гладких и шероховатых трубах.

Состояние стенок трубы в значитель­ной мере влияет на поведение жидкости в турбу­лентном потоке. Так при ламинарном движении жидкость движется медленно и плавно, спокойно обтекая на своём пути незначительные препятст­вия. Возникающие при этом местные сопротивления настолько ничтожны, что их величи­ной можно пренебречь. В турбулентном же потоке такие малые препятствия служат ис­точником вихревого движения жидкости, что приводит к возрастанию этих малых мест­ных гидравлических сопротивлений, которыми мы в ламинарном потоке пренебрегли. Та­кими малыми препятствиями на стенке трубы являются её неровности. Абсолютная вели­чина таких неровностей зависит от качества обработки трубы. В гидравлике эти неровно­сти называются выступами шероховатости, они обозначаются литерой D.

В зависимости от соотношения толщины ламинарной плёнки и величины выступов шероховатости будет меняться характер движения жидкости в потоке. В случае, когда толщина ламинарной плёнки велика по сравнению с величиной выступов шероховатости (, выступы шероховатости погружены в ламинарную плёнку и турбулентному ядру течения они недоступны (их наличие не сказывается на потоке). Такие трубы называются гидравлически гладкими. Когда размер выступов шероховатости превышает толщину ламинарной плёнки, то плёнка теряет свою сплошность, и выступы шероховатости становятся источником многочисленных вихрей, что существенно сказы­вается на потоке жидкости в целом. Такие трубы называются гидравлически шероховаты­ми. Естественно, существует и проме­жуточный вид шероховатости стенки трубы, когда выступы шероховатости становятся соизмеримыми с толщиной ламинарной плёнки d≈D.

 

 

 

.

 

 

Билет 6

 

2. Понятие давления в жидкости. Единицы измерения, их соотношение в различных системах единиц, указать размерность.

Сам.раб. 3. Полный дифференциал давления по Эйлеру. Математическое выражение, применение в гидромеханики.

 

2)

Давлением в газе (или жидкости) называется величина, равная отношению модуля силы F, действующей по нормали к плоской поверхности, к площади этой поверхности S:

(1.1)

За единицу давления принимается такое давление, которое производит сила в 1 Н, действующая на поверхность площадью 1 перпендикулярно этой поверхности и называется паскалем (обозначается Па).

Используются также другие единицы давления: гектопаскаль (гПа) и килопаскаль (кПа).

1 кПа=1000 Па; 1 гПа = 100 Па; 1 Па =0,001 кПа; 1 Па 0,01 гПа

Установленный в XVIII веке Б.Паскалем (1623-1662) один из основополагающих законов гидростатики, известный как закон Паскаля, утверждает: если на жидкость (или газ), заключенную в замкнутый сосуд производить давление, то это давление передается по всем направлениям во все точки жидкости (газа) и на любую часть внутренней поверхности сосуда без изменения.

Свойство передавать без изменения давление связано с несжимаемостью жидкости (например, воды) при больших усилиях. Достаточно отметить, что сжатие воды, в частности, под действием атмосферного давления приводит к уменьшению ее объема на

1/20 000 часть исходного объема. В связи с этим в физике вводится представление о "несжимаемости" жидкости, подобно тому, как используется понятие абсолютно твердого тела в механике.

Рассмотрим следующую ситуацию, иллюстрирующую закон Паскаля. Возьмем сосуд, наполненный жидкостью (к примеру, водой), находящейся под неизменным давлением создаваемым некоторой силой F, приложенной к поршню с площадью S, закрывающему открытую часть сосуда. Перед тем как закрыть сосуд поршнем поместим в жидкость небольшой полый кубик (например, объемом 1 см³) с тонкими металлическими стенками и площадью грани S_k. На каждую грань этого кубика согласно закону Паскаля будет действовать сила F_k =p · S_k независимо от его ориентации. Если жидкость покоится, то в любой ее малой по размерам части давление будет одинаковым во всех направлениях. Будь это не так, на небольшой кубик в жидкости действовала бы отличная от нуля результирующая сила, и он пришел бы в движение, что противоречит исходному условию равновесия жидкости. Следовательно, 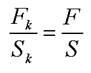или Ниже будет показано, что данное соотношение лежит в основе работы гидравлического пресса.

Все эти рассуждения, демонстрирующие закон Паскаля, справедливы в отсутствие силы тяжести, или когда можно ею пренебречь. В этом случае давление во всех точках сосуда будет одинаковым, независимо от формы последнего.

В поле тяжести Земли давление жидкости возрастает с глубиной и численно равно на глубине h весу столба жидкости высотой h и площадью 1 см² .

Давление, которое появляется в жидкости из-за наличия поля тяжести, называется гидростатическим.

Уравнение (1.2) позволяет построить график зависимости давления в жидкости от глубины погружения (рис.1). Так как давление прямо пропорционально глубине h, то его график представляет собой прямую линию (линейную функцию), где Понятно, что наклон прямой давления на графике зависит от плотности жидкости: чем она больше, тем больше давление на одной и той же глубине. На рис. 1 поэтому на глубине h. Если на поверхность жидкости оказывается еще и дополнительное давление, например, земной атмосферы, то полное давление на глубине h будет равно .

Тогда нетрудно найти разность давлений на двух уровнях жидкости, отстоящих друг от друга по вертикали на расстоянии h ₁, что и будет составлять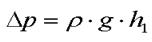

Это, в частности, приводит к тому, что в сообщающихся сосудах, заполненных однородной жидкостью, давление во всех точках жидкости, расположенных на одном уровне, одинаково, независимо от формы сосудов, если наружное давление для всех сосудов одинаково (см. рис.2).

Поэтому в поле тяжести давление в любой точке сосуда не зависит от формы сосуда, а зависит лишь от глубины и плотности жидкости.

Важным следствием предыдущих рассуждений является закон сообщающихся сосудов. Если наливать жидкость в один из сосудов, изображенных на рис.2, то, перетекая через соединения в остальные сосуды, жидкость установится во всех сосудах на одном уровне. Это объясняется тем, что давление на свободных поверхностях жидкости в сосудах одно и то же и равно атмосферному. Вследствие этого все свободные поверхности должны находиться в одной горизонтальной плоскости.

Принцип сообщающихся сосудов используется в устройстве водомерных трубок современных электрочайников и кофеварок. Вода в них устанавливается на том же уровне, что и в объеме чайника. Если на этой трубке нанесены деления, то всегда можно контролировать заливаемый объем воды.

Другая ситуация наблюдается, когда имеются сообщающиеся сосуды с разными жидкостями. Для рассмотрения этого случая возьмем U-образную трубку с открытыми концами и зальем сначала воду с плотностью 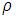. Совершенно ясно, что уровень воды в обоих коленах будет одинаков. Доливая теперь в одно из колен другую жидкость, к примеру керосин (с плотностью ), который не смешивается с водой, мы заметим, что уровни жидкостей в каждом колене поднимутся, но уже не одинаково (рис.3).

Поверхность раздела между жидкостями (на рис. 3 — уровень АВ) по мере доливания второй жидкости будет опускаться, и вследствие этого возникнет разность уровней h₁ и h₂ жидкостей в коленах U-образной трубки относительно границы раздела АВ.

Определим соотношение между высотами жидкостей в каждом из сосудов над уровнем АВ. Ниже этого уровня в сосудах находится одна и та же жидкость, поэтому давления p_A и p_B в точках А и В, лежащих на одной высоте должны быть одинаковыми. С другой стороны, эти давления равны, исходя из соотношения (1.3)

где p₀ — атмосферное давление. Приравнивая p_A и p_B , получим

то есть в сообщающихся сосудах высоты столбов жидкостей над уровнем раздела обратно пропорциональны их плотностям. При равенстве давлений высота столба жидкости с большей плотностью будет меньше высоты столба жидкости с меньшей плотностью.

В практике для измерения атмосферного давления используют металлический барометр, называемый анероидом (в переводе с греческого — безжидкостный). Так барометр называют потому, что он не содержит ртути). Для измерения давлений, больших или меньших атмосферного, используют манометры (от греческих слов: м а н о с — редкий, неплотный, м е т р е о — измеряю). Одним из примеров использования закона сообщающихся сосудов является открытый (жидкостной) манометр, который как раз и состоит из U-образной трубки, заполненной ртутью или другой жидкостью. На одно колено наносится шкала в сантиметрах или миллиметрах, а к другому колену подводится, к примеру, сжатый воздух. Под действием этого воздуха ртуть в одном колене опускается, в другом — поднимается, и возникает разность уровней. Зная разность высот и учитывая удельную плотность ртути, легко найти давление.

 

 

Билет 7

 

2. Ламинарное движение жидкости в плоских границах. Расход жидкости через плоские и кольцевые щели.

 

3. Использование уравнения Бернулли для измерения скорости потока жидкости. Трубка Пито, схема, рабочие формулы.

 

2) Ламина́рное тече́ние (лат. lamina — пластинка, полоска) — течение, при котором жидкость или газ перемещается слоями без перемешивания и пульсаций (то есть беспорядочных быстрых изменений скорости и давления).

Ламинарное течение возможно только до некоторого критического значения числа Рейнольдса, после которого оно переходит в турбулентное. Критическое значение числа Рейнольдса зависит от конкретного вида течения (течение в круглой трубе, обтекание шара и т. п.).

Например, для течения в круглой трубе .

 

озьмем трубу неодинакового сечения (рис. 311) и будем пропускать через нее постоянный поток воды. По уровням в манометрических трубках мы увидим, что в суженных

Рис. 311. В узких частях трубы статическое давление текущей жидкости меньше, чем в широких
местах трубы статическое давление меньше, чем в широких. Значит, при переходе из широкой части трубы в более узкую степень сжатия жидкости, уменьшается (давление уменьшается), а при переходе из более узкой части в широкую — увеличивается (давление увеличивается).

Это объясняется тем, что в широких частях трубы жидкость должна течь медленнее, чем в узких, так как количество жидкости, протекающей за одинаковые промежутки времени, одинаково для всех сечений трубы. Поэтому при переходе из узкой части трубы в широкую скорость жидкости уменьшается: жидкость тормозится, как бы натекая на препятствие, и степень сжатия ее (а также ее давление) растет. Наоборот, при переходе из широкой части трубы в узкую скорость жидкости увеличивается и сжатие ее уменьшается: жидкость, ускоряясь, ведет себя подобно распрямляющейся пружине.

Итак, мы видим, что давление жидкости, текущей по трубе, больше там, где скорость движения жидкости меньше, и обратно: давление меньше там, где скорость движения жидкости больше. Эту зависимость между скоростью жидкости и ее давлением называют законом Бернулли по имени швейцарского физика и математика Даниила Бернулли (1700—1782). Закон Бернулли имеет место и для жидкостей и для газов. Он остается в силе и для движения жидкости, не ограниченного стенками трубы,— в свободном потоке жидкости. В этом случае закон Бернулли нужно применять следующим образом.

Допустим, что движение жидкости или газа не изменяется с течением времени (установившееся течение). Тогда мы можем представить себе внутри потока линии, вдоль которых происходит движение жидкости. Эти линии называются линиями тока; они разбивают жидкость на отдельные струи, которые текут рядом, не смешиваясь, Линии тока можно сделать видимыми, вводя в поток воды жидкую краску через тонкие трубочки. Струйки краски располагаются вдоль линий тока. В воздухе для получения видимых линий тока можно воспользоваться струйками дыма. Можно показать, что закон Бернулли применим для каждой струи в отдельности: давление больше в тех местах струи, где скорость в ней меньше и, следовательно, где сечение струи больше, и обратно. Из рис. 311 видно, что

Рис. 312. Воздух засасывается в узкую часть трубы, где давление меньше атмосферного
сечение струи велико в тех местах, где линии тока расходятся; там же, где сечение струи меньше, линии тока сближаются. Поэтому закон Бернулли можно сформулировать еще так: в тех местах потока, где линии тока гуще, давление меньше, а в тех местах, где линии тока реже, давление больше.

Возьмем трубу, имеющую сужение, и будем пропускать по ней с большой скоростью воду. Согласно закону Бернулли, в суженной части давление будет понижено. Можно так подобрать форму трубы и скорость потока, что в суженной части давление воды будет меньше атмосферного. Если теперь присоединить к узкой части трубы отводную трубку (рис. 312), то наружный воздух будет засасываться в место с меньшим давлением: попадая в струю, воздух будет уноситься водой. Используя это явление, можно построить разрежающий насос — так называемый водоструйный насос. В изображенной на рис. 313 модели водоструйного насоса засасывание воздуха производится через кольцевую щель 1,

Рис. 313. Схема водоструйного насоса
вблизи которой вода движется с большой скоростью. Отросток 2 присоединяется к откачиваемому сосуду. Водоструйные насосы не имеют движущихся твердых частей (как, например, поршень в обычных насосах), что составляет одно из их преимуществ.

Будем продувать воздух по трубке с сужением (рис.314). При достаточной скорости воздуха давление в суженной части трубки будет ниже атмосферного. Жидкость из сосуда будет засасываться в боковую трубку. Выходя из трубки, жидкость будет распыляться струей воздуха. Этот прибор называется пульверизатором — распылителем.

Рис. 314. Пульверизатор

 

3) Трубка Пито — прибор для измерения динамического напора текущей жидкости (суспензии) или газа. Названа по имени её изобретателя (1732) французского учёного А. Пито (Н. Pitot).

Представляет собой Г-образную трубку. Установившееся в трубке избыточное давление приближённо равно:

где — плотность движущейся (набегающей) среды; — скорость набегающего потока; — коэффициент.

Напорная (пневмометрическая, или трубка полного напора) трубка Пито подключается к специальным приборам и устройствам. Применяется при определении относительной скорости и объёмного расхода в газоходах и вентиляционных системах в комплекте с дифференциальными манометрами.

Применяется как составная часть трубки Прандтля в авиационных приёмниках воздушного давления для возможности одновременного определения скорости и высоты полёта.

 

Для измерения скорости в любой точке потока широко используется трубка Пито (рисунок), принцип работы которой основан на использовании уравнения Бернулли. Пусть требуется измерить скорость жидкости в какой-то точке потока. Поместив конец трубки в указанную точку и составив уравнение Бернулли для сечения 1 - 1 и сечения, проходящего на уровне жидкости в трубке Пито.

 

⇐ Предыдущая123456

Поделиться:

Воспользуйтесь поиском по сайту: