 |
Производная и её приложения
|
|
|
|
141-150. Найти производные  данных функций.
данных функций.
141. а)  ; б)
; б) 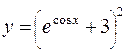 ;
;
в) 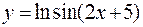 ; г)
; г)  ; д)
; д)  .
.
142. а)  ; б)
; б)  ; в)
; в) 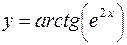 ;
;
г) 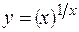 ; д)
; д) 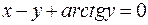 .
.
143. а)  ; б)
; б)  ; в)
; в) 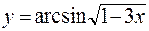 ;
;
г)  ; д)
; д)  .
.
144. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
145. а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д) 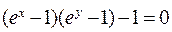 .
.
146. а) 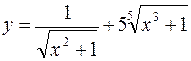 ; б)
; б)  ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
147. а)  ; б)
; б)  ;
;
в) 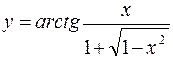 ; г)
; г)  ; д)
; д)  .
.
148. а)  ; б)
; б) 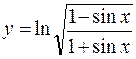 ;
;
в)  ; г)
; г)  ; д)
; д) 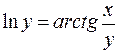 .
.
149. а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  .
.
150. а)  ; б)
; б) 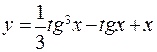 ;
;
в)  ; г)
; г)  ;
;
д)  .
.
101-110. Исследовать методами дифференциального исчисления функцию и, используя результаты исследования, построить ее график.
191.  . 192.
. 192.  .
.
193.  . 194.
. 194.  .
.
195.  . 196.
. 196.  .
.
197. 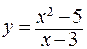 . 198.
. 198.  .
.
199.  . 200.
. 200.  .
.
Дифференциальное исчисление функций нескольких переменных
231. Дана функция  .
.
Показать, что  .
.
232. Дана функция 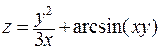 .
.
Показать, что  .
.
233. Дана функция  .
.
Показать, что  .
.
234. Дана функция  .
.
Показать, что  .
.
235. Дана функция  .
.
Показать, что 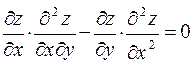 .
.
236. Дана функция  . Показать, что
. Показать, что  .
.
237. Дана функция  .
.
Показать, что  .
.
238. Дана функция 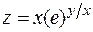 .
.
Показать, что  .
.
239. Дана функция 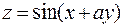 .
.
Показать, что  .
.
240. Дана функция  .
.
Показать, что 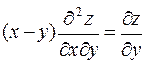 .
.
251-260. Найти наименьшее и наибольшее значения функции z=f(x, y) в замкнутой области D, заданной системой неравенств. Сделать чертеж.
251. z=x 2 +y 2 - 9 xy+ 27; 0≤ x ≤3, 0≤ y ≤3.
252. z=x 2 + 2 y 2 + 1; x ≥0, y ≥0, x + y ≤3.
253. z= 3-2 x 2 -xy - y 2; x ≤1, у ≤ х, у ≥0.
254. z=x 2 + 3 y 2+x-y; x ≥1, y ≥-1, х+y ≤1.
255. z=x 2 + 2 xy +2 y 2; -1≤ x ≤1, 0≤ y ≤2.
256. z= 5 x 2 - 3 xy + y 2 + 4; x ≥-1, y ≥-1, х+y ≤1.
257. z= 10+2 xy - x 2; 0≤ y ≤4- x 2.
258. z=x 2+2 xy -y 2 + 4 x; x ≤0, y ≤0, х+y +2≥0.
259. z=x 2 + xy -2; 4 x 2-4≤ y ≤0.
260. z=x 2+ xy; -1≤ x ≤1, 0≤ y ≤3.
261-270. Дана функция z=z(x, y), точка А(х0, у0) и вектор  . Найти: 1)
. Найти: 1)  в точке A; 2) производную в точке A по направлению вектора
в точке A; 2) производную в точке A по направлению вектора  .
.
261. 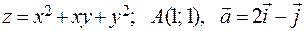 .
.
262.  .
.
263.  .
.
264. 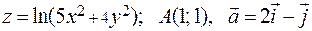 .
.
265.  .
.
266.  .
.
267.  .
.
268.  .
.
269.  .
.
270.  .
.
Неопределённый и определённый интегралы
281-290. Найти неопределенные интегралы. В двух примерах (пункты а и б) проверить результаты дифференцированием.
|
|
|
281. а)  ; б)
; б) 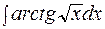 ;
;
в)  ; г)
; г)  .
.
282. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
283. а)  ; б)
; б) 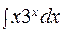 ;
;
в)  ; г)
; г)  .
.
284. а)  ; б)
; б)  ;
;
в) 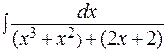 ; г)
; г) 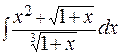 .
.
285. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
286. а)  ; б)
; б) 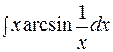 ;
;
в)  ; г)
; г)  .
.
287. а)  ; б)
; б) 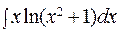 ;
;
в)  ; г)
; г)  .
.
288. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 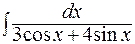 .
.
289. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
290. а)  ; б)
; б) 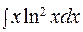 ;
;
в) 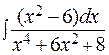 ; г)
; г) 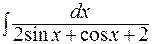 .
.
301-310. Вычислить несобственный интеграл или доказать его расходимость.
30 1.  . 30 2.
. 30 2. 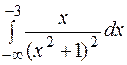 .
.
30 3.  . 30 4.
. 30 4.  .
.
30 5.  . 306.
. 306.  .
.
30 7.  .
.  30 8.
30 8.  .
.
30 9.  . 310.
. 310.  .
.
Дифференциальные уравнения
321-330. Найти общее решение дифференциального уравнения.
321. 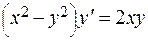 . 322.
. 322.  .
.
323.  . 324.
. 324.  .
.
325.  . 326.
. 326.  .
.
327. 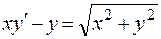 . 328.
. 328.  .
.
329. 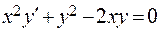 . 330.
. 330.  .
.
341-350. Найти частное решение дифференциального уравнения 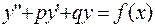 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 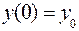 ,
,  .
.
341. 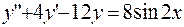 ;
; 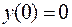 ,
,  .
.
342.  ;
;  ,
, 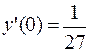 .
.
343.  ;
; 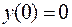 ,
,  .
.
344. 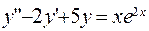 ;
;  ,
,  .
.
345.  ;
;  ,
, 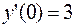 .
.
346. 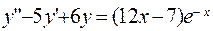 ;
; 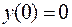 ,
,  .
.
347. 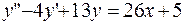 ;
;  ,
,  .
.
348.  ;
;  ,
, 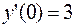 .
.
349. 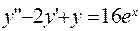 ;
;  ,
,  .
.
350. 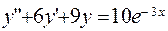 ;
;  ,
,  .
.
Двойные и криволинейные интегралы
351-360. Вычислить двойные интегралы по области D.
351. 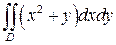 , где D – область, ограниченная линиям
, где D – область, ограниченная линиям 
352.  , где D – область, ограниченная линиями
, где D – область, ограниченная линиями 
353.  , где D – область, ограниченная линиями
, где D – область, ограниченная линиями 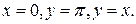
354.  , где D – область, ограниченная линиями
, где D – область, ограниченная линиями 
355.  где D – область, ограниченная линиями
где D – область, ограниченная линиями 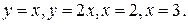
356.  , где D – область, ограниченная линиями
, где D – область, ограниченная линиями 
357.  где D – область, ограниченная линиями
где D – область, ограниченная линиями 
358.  где D – область, ограниченная линиями
где D – область, ограниченная линиями 
359.  , где D – область, ограниченная линиями
, где D – область, ограниченная линиями 
360.  где D – область, ограниченная линиями
где D – область, ограниченная линиями
 .
.
361 – 370. Перейдя к полярным координатам, вычислить площадь фигуры, ограниченной областью D.
361. Область D ограниченна линиями:  (І четв.)
(І четв.)
362. Область D ограниченна линиями: 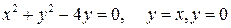 .(І четв.)
.(І четв.)
363. Область D ограниченна линиями:  . (І четв.)
. (І четв.)
364. Область D ограниченна линиями: 
365. Область D ограниченна лемнискатой:  (І четв.)
(І четв.)
366. Область D ограниченна линиями: 
367. Область D ограниченна линиями: 
368. Область D ограниченна линиями: 
369. Область D ограниченна линиями: 
370. Область D ограниченна лемнискатой: 
371 – 380. Вычислить криволинейные интегралы
371.  где L – контур треугольника, образованного осями координат и прямой
где L – контур треугольника, образованного осями координат и прямой  в положительном направлении, т.е. против движения часовой стрелки.
в положительном направлении, т.е. против движения часовой стрелки.
372.  где L – дуга параболы
где L – дуга параболы  от точки О (0;0) до точки
от точки О (0;0) до точки
|
|
|
А(2;4).
373.  где L – контур прямоугольника, образованного прямыми
где L – контур прямоугольника, образованного прямыми
 в положительном направлении (против часовой стрелки).
в положительном направлении (против часовой стрелки).
374.  вдоль кривой
вдоль кривой  .
.
375.  вдоль кривой
вдоль кривой  от точки О (0;0) до точки А(1;1).
от точки О (0;0) до точки А(1;1).
376.  вдоль
вдоль  отточки О (0;0) до точки А(1;1).
отточки О (0;0) до точки А(1;1).
377.  , где L – четверть окружности
, где L – четверть окружности  0
0  , против часовой стрелки.
, против часовой стрелки.
378.  , где L – первая арка циклоиды
, где L – первая арка циклоиды  0
0  .
.
379.  вдоль линии
вдоль линии  от точки О (0;0) до точки А(1;1).
от точки О (0;0) до точки А(1;1).
380.  вдоль отрезка ОА, О (0;0),
вдоль отрезка ОА, О (0;0),  .
.
Ряды
421-430. Исследовать сходимость числового ряда.
421.  . 422.
. 422. 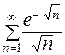 .
.
423.  . 424.
. 424.  .
.
425. 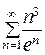 . 426.
. 426. 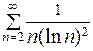 .
.
427.  . 428.
. 428.  .
.
429.  . 430.
. 430. 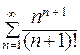 .
.
431-440. Найти интервал сходимости степенного ряда.
431.  . 432.
. 432.  .
.
433. 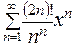 . 434.
. 434.  .
.
435.  . 436.
. 436.  .
.
437.  . 438.
. 438.  .
.
439.  . 440.
. 440.  .
.
441-450. Вычислить определенный интеграл  с точностью до 0,001, разложив подынтегральную функцию в ряд, и, затем, проинтегрировав ее почленно.
с точностью до 0,001, разложив подынтегральную функцию в ряд, и, затем, проинтегрировав ее почленно.
441.  . 442.
. 442.  .
.
443.  . 444.
. 444.  .
.
445. 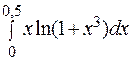 . 446.
. 446.  .
.
447. 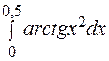 . 448.
. 448.  .
.
449.  . 450.
. 450.  .
.
451 – 460. Найти три первых отличных от нуля члена разложения в степенной ряд решения 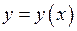 дифференциального уравнения
дифференциального уравнения 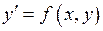 , удовлетворяющего начальному условию
, удовлетворяющего начальному условию  .
.
451. 
452. 
453. 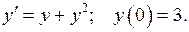
454. 
455. 
456. 
457. 
458. 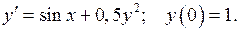
459. 
460. 
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ ВЫПОЛНЕНИЯ ЗАДАНИЙ
В данном разделе приведены образцы выполнения заданий, содержащихся в контрольных работах.
Задания 11 – 20
Для решения задач 11 – 20 рекомендуется учебное пособие [5]
Гл. I –IV, стр.39 – 91.
В пирамиде SABC: треугольник АВС – основание пирамиды, точка S – ее вершина. Даны координаты точек A, B, C, S. Сделать чертеж. Найти:
1. длину ребра АВ;
2. угол между ребрами АВ и AS;
3. угол наклона ребра AS к основанию пирамиды;
4. площадь основания пирамиды;
5. объем пирамиды;
6. уравнение прямой АВ;
7. уравнение плоскости АВС;
8. проекцию вершины S на плоскость АВС;
9. длину высоты пирамиды
SABC: А(-3;0;0); В(0;2;0); С(0;0;6); S(-3;4;5).
Решение
1) Длину ребра АВ находим по формуле расстояния между двумя точками:

2) Угол между рёбрами  найдём по формуле косинуса угла между векторами
найдём по формуле косинуса угла между векторами 
 , координаты которых определяются так:
, координаты которых определяются так:
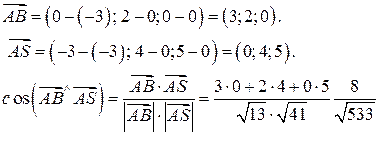


3) Найдем координаты вектора 

Найдем координаты вектора 

Он перпендикулярен плоскости (грани) ABC, поэтому угол  между ребром AS и гранью ABC является дополнительным к углу α между векторами
между ребром AS и гранью ABC является дополнительным к углу α между векторами 

 α
α
φ
Отсюда получаем

4) Площадь  определяем с помощью векторного произведения:
определяем с помощью векторного произведения:
 ,
,

5) Объём пирамиды  находится через вычисление смешанного произведения векторов
находится через вычисление смешанного произведения векторов  Изучите понятие смешанного произведения, формулу объёма пирамиды и формулу для вычисления смешанного произведения трёх векторов. Формула для нахождения объема V пирамиды:
Изучите понятие смешанного произведения, формулу объёма пирамиды и формулу для вычисления смешанного произведения трёх векторов. Формула для нахождения объема V пирамиды:
|
|
|

7) Запишем уравнение плоскости (ABC) перпендикулярной вектору  , проходящей через точку А(-3;0;0)
, проходящей через точку А(-3;0;0)

6) Уравнение прямой 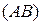 , проходящей через точки
, проходящей через точки 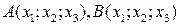


Канонические уравнения прямой, вектор  направляющий вектор прямой
направляющий вектор прямой 
7) Запишем уравнение плоскости (ABC) перпендикулярной вектору  , проходящей через точку А(-3;0;0)
, проходящей через точку А(-3;0;0)

8) Для определения проекции вершины  на плоскость
на плоскость  выполняютсяследующие действия:
выполняютсяследующие действия:
а) составляется уравнение высоты пирамиды  .
.
б) находится точка пересечения высоты и основания  решением системы, содержащей уравнение высоты и уравнение плоскости.
решением системы, содержащей уравнение высоты и уравнение плоскости.
Решение: SO –высота пирамиды, перпендикулярна плоскости (ABC), следовательно, прямая (SO) параллельна вектору  или
или 
 - нормали плоскости (ABC.
- нормали плоскости (ABC. 
Он будет направляющим для 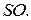 По уравнению
По уравнению  координаты вершины
координаты вершины  , т.е.
, т.е. 
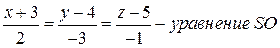 . Так как точка О – пересечение прямой (SO) и плоскости (ABC), то ее координаты удовлетворяют системе уравнений
. Так как точка О – пересечение прямой (SO) и плоскости (ABC), то ее координаты удовлетворяют системе уравнений
 , которую можно решить подстановкой
, которую можно решить подстановкой

Подставив во второе уравнение, найдём значение 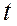 , и следовательно значения
, и следовательно значения



Точка  - проекция точки
- проекция точки  на плоскость
на плоскость 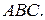
9) Длину высоты  пирамиды можно найти по формуле расстояния
пирамиды можно найти по формуле расстояния  между точками S и O или по формуле расстояния d от точки
между точками S и O или по формуле расстояния d от точки  до плоскости
до плоскости  :
:

Изучите формулы самостоятельно, решив задание 9).
Задания 51 – 60
Дана система линейных уравнений

Решить систему а) матричным методом, б) методом Крамера, в) методом Гаусса.
а) Матричный метод
Данной системе соответствует матричное уравнение  , которое решается по формуле:
, которое решается по формуле:  . Матрицы имеют вид:
. Матрицы имеют вид:

Находим обратную матрицу


Находим матрицу 
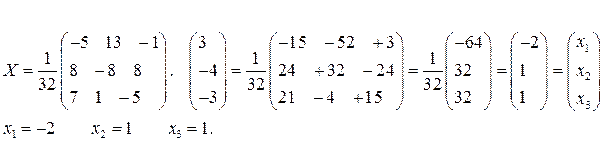
б) Метод Крамера
 - формулы Крамера.
- формулы Крамера.
Вычислим все определители
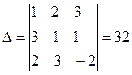


в) Метод Гаусса
Составим расширенную матрицу 
 и преобразуем её с помощью элементарных преобразований.
и преобразуем её с помощью элементарных преобразований.
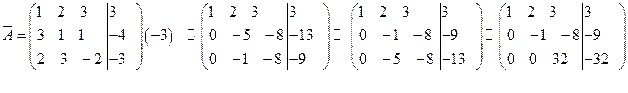
Из полученной матрицы, выделяя последнюю строку, видим, что исключены неизвестные  и
и  . Найдём
. Найдём 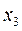 .
. 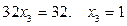 .
.
|
|
|
Вторая строка соответствует уравнению:
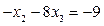 или
или 
Аналогично из первой строки напишем уравнение:
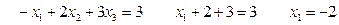
Итак: 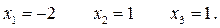
Задания 91 – 100.
Дано комплексное число 
Записать число  в геометрической и тригонометрической формах и найти все корни уравнения
в геометрической и тригонометрической формах и найти все корни уравнения 
Рекомендуемая литература: Данко П.Е., Кожевникова Т.Я. Высшая математика в упражнениях и задачах, ч. II, гл.III, §7, стр.97 – 101.
Найдём алгебраическую форму комплексного числа

Тригонометрическая форма комплексного числа  определится по формуле
определится по формуле  .
.
Изобразив число на плоскости, найдём 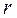 и
и  .
. 



 -1
-1 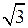
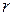


Итак, число 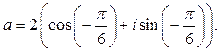
Найдём корни уравнения 
 вычислим по формуле Муавра
вычислим по формуле Муавра

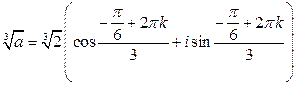


Задания 111 – 120
Вычислить пределы:
а) 
За скобку выносили наивысшую степень  для числителя и знаменателя.
для числителя и знаменателя.
б) 
Для исключения неопределённости  требуется числитель и знаменатель разложить на множители.
требуется числитель и знаменатель разложить на множители.
в) 
В данном случае для исключения неопределённости  использованы эквивалентные бесконечно малые,например
использованы эквивалентные бесконечно малые,например 
г) 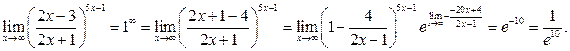
д) Числитель и знаменатель умножаем на выражение, сопряжённое числителю.

Задания 111 – 120
Задана функция  Найти точки разрыва, если они существуют.
Найти точки разрыва, если они существуют.
Сделать чертёж.
 .
.
Кусочно-заданная функция представлена функциями, непрерывными на данных интервалах.
Проверим непрерывность в граничных точках.
 найдём односторонние пределы
найдём односторонние пределы
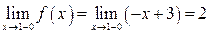

Левосторонний и правосторонний пределы равны и равны значению функции в точке 
 . Значит функция в этой точке непрерывна.
. Значит функция в этой точке непрерывна.
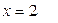 аналогично
аналогично

Пределы различны, значит в точке  функция имеет разрыв с конечным скачком.
функция имеет разрыв с конечным скачком.
График функции выполните самостоятельно.
Обратите внимание на учебное пособие [5], ч.I, гл.IV, §§4 – 6.
Задания 141– 150
Найти производные  следующих функций:
следующих функций:
а) 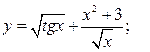 б)
б) 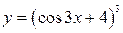 ;
;
в)  г)
г)  ;
;
д)  .
.

б) 
в) 
г) 
Прологарифмируем обе части равенства

Продифференцируем обе части равенства
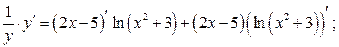


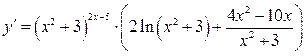
д) 
Функция  задана неявно. Учитываем, что
задана неявно. Учитываем, что  аргумент,
аргумент,  функция.
функция.

Задания 151 – 160
Найти 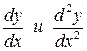 функций:
функций:

Решение:
а) 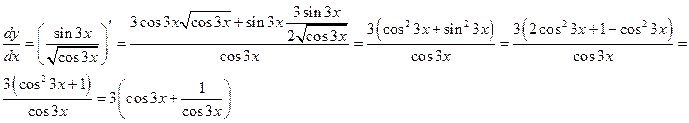

б) 

Задания 191 – 200
Исследовать методами дифференциального исчисления функцию и построить её график.

Рассмотрим свойства функции:
1. Область определения: 
2. Чётностьь, нечётность функции: 
Функция общего вида.
3. Асимптоты.
а) Так как  , то прямая
, то прямая  является вертикальной асимптотой:
является вертикальной асимптотой:

б)  – наклонная асимптота.
– наклонная асимптота.
Найдём 
Найдём 
 – уравнение наклонной асимптоты.
– уравнение наклонной асимптоты.
4. Найдём точки экстремума и интервалы монотонности функции:


Так как 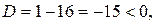 то действительных корней нет, значит, нет точек экстремума.
то действительных корней нет, значит, нет точек экстремума.
Производная  на всей области определения, значит функция
на всей области определения, значит функция
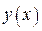 убывает.
убывает.
|
|
|
5. Точки пересечения с координатными осями
а) с осью 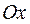 при
при 
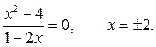 ,
,
б) с осью 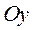 при
при 
 .
.
Используя исследование функции, строим график (схематично).

 Задания 141-150, 151-160, 191-200 легко выполнить, используя учебное пособие [5]? Высшая математика в упражнениях и задачах ч.I гл. VII §§ 1-2 стр. 151-183.
Задания 141-150, 151-160, 191-200 легко выполнить, используя учебное пособие [5]? Высшая математика в упражнениях и задачах ч.I гл. VII §§ 1-2 стр. 151-183.

Задания 231-240
Показать, что функция 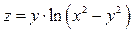 удовлетворяет равенству:
удовлетворяет равенству:

Находим частные производные по  и по
и по  :
:

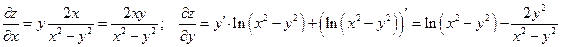
Подставим в равенство частные производные.
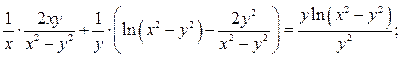
 ;
;

Равенство верно.
Задания 251-260
Найти наименьшее и наибольшее значения функции 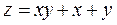
в области D =(ABCD): 
 y
y



