 |
Дифференциальные уравнения движения вязкой жидкости
|
|
|
|
Относительный покой жидкости при равноускоренном прямолинейном движении резервуара.
Относительный покой жидкости в цилиндрическом вращающемся сосуде.
Относительный покой жидкости. Вращающийся сосуд.
Понятие относительного покоя.
Под этим определением подразумевается, что частицы жидкости, заключенной в некотором сосуде, не имеют перемещений друг относительно друга и вся масса жидкости покоится относительно стенок сосуда, следовательно, относительно жестко связанных с сосудом координатных осей, в то же время сосуд перемещается произвольным образом относительно неподвижной системы отсчета.
Относительный покой однородной жидкости в цилиндрическом сосуде, вращающемся вокруг вертикальной оси с постоянной угловой скоростью
Давление в любой точке жидкости (например, в т. А), находящейся во вращающемся сосуде определяется по формуле:
Уравнение изобарической поверхности:
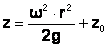
Прямолинейное равноускоренное движение сосуда с жидкостью
Давление в любой точке жидкости плотностью r, находящейся в сосуде, движущемся с постоянным ускорением а, определяется по формуле:
,
где H – уровень жидкости в покоящемся сосуде, ро - поверхностное давление.
Уравнение поверхности уровня (изобарической)
Виды движения жидкости.
В движущейся жидкости скорость v и давление p могут изменяться в пространстве и во времени:
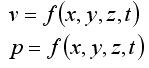
в связи с этим различают виды движения:
Неустановившееся – вид движения,при котором давление и скорость изменяются во времени и в пространстве.
Уровень в сосуде будет падать и скорость потока будет изменяться во времени. Одновременно с каждый момент времени скорость v в разных частях трубопровода из за его сужения будет разной (так же как и давление p).
|
|
|
Установившееся (стационарное) – вид движения, при котором давление и скорость постоянны во времени, а изменяются только в пространстве.
В сосуд добавляют воду по мере её вытекания, таким образом скорость изменяется только из-за сужения трубопровода (увеличивается к концу), то есть изменяется только в пространстве.
Скорость и давление в каждой точке потока постоянны.
Равномерное – вид движения, при котором давление и скорость постоянны во времени и в пространстве.
Также различают напорное и безнапорное движение жидкости.
Напорное движение – в потоке отсутствует свободная поверхность.
Безапорное движение – в потоке имеется свободная поверхность.
15. Уравнение неразрывности потока жидкости. Рассмотрим установившийся поток жидкости между живым сечением 1 и 2.
. 
Объемный расход жидкости вытекающей через живое сечение 1: 
, где v1-средняя скорость в 1 сечении. Объемный расход жидкости вытекающей через живое сечение 2: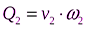 
, ω2 площадь 2го сечения.
Поскольку форма потока жидкости между 1 и 2 сечениями в течении времени не меняется жидкость не сжимается и в ней не возможно образование пустот, то объем вытекающей жидкости Q1 должен быть равен вытекающей жидкости Q2: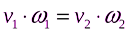 
- уравнение неразрывности.
, т.е. средняя скорость потока обратно пропорционально площадям соответствующих живых потоков
Для газов поскольку они сжимаются массовый расход газа вытекающего через 1 живое сечение: 
, где ρ1 плотность газа в 1ом сечении. А массовый расход газа вытекающего через 2ое сечение 
Масса вытекающего газа должна быть равной массе вытекающего газа: 
уравнение неразрывности для газов.
Дифференциальные уравнения движения вязкой жидкости
Уравнение Эйлера служит одним из фундаментальных в гидравлике, наряду с уравнением Бернулли и некоторыми другими.
|
|
|
Изучение гидравлики как таковой практически начинается с уравнения Эйлера, которое служит исходным пунктом для выхода на другие выражения.
Попробуем вывести это уравнение. Пусть имеем бесконечно малый параллелепипед с гранями dxdydz в невязкой жидкости с плотностью ρ. Он заполнен жидкостью и движется как составная часть потока. Какие силы действуют на выделенный объект? Это силы массы и силы поверхностных давлений, которые действуют на dV = dxdydz со стороны жидкости, в которонаходится выделенный dV. Как силы массы пропорциональны массе, так и поверхностные силы пропорциональны площадям, на которые оказывается давление. Эти силы направлены к граням вовнутрь по нормали. Определим математическое выражение этих сил.
Назовем, как и при получении уравнения неразрывности, грани параллелепипеда:
1, 2 – перпендикулярные к оси ОХ и параллельные оси ОY;
3, 4 – перпендикулярные к оси OY и параллельные оси ОХ;
5, 6 – перпендикулярные к оси OZ и параллельные оси ОХ.
Теперь нужно определить, какая сила приложена к центру масс параллелепипеда.
Сила, приложенная к центру массы параллелепипеда, которая и заставляет эту жидкость совершать движение, есть сумма найденных сил, то есть
Получили уравнение движения параллелепипеда с dV1 по направлению оси Х.
Делим (1) на массу ρdxdydz:
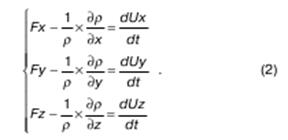
Полученная система уравнений (2) есть искомое уравнение движения невязкой жидкости – уравнение Эйлера.
К трем уравнениям (2) добавляются еще два уравнения, поскольку неизвестных пять, и решается система из пяти уравнений с пятью неизвестными: одним из двух дополнительных уравнений является уравнение неразрывности. Еще одним уравнением является уравнение состояния. Например, для несжимаемой жидкости уравнением состояния может быть условие ρ = const.
Уравнение состояния должно быть выбрано таким образом, чтобы оно содержало хотя бы одно из пяти неизвестных.
|
|
|
