 |
Термодинамическая модель обогревателя
|
|
|
|
В данном проекте предполагается, что обогреватель выдает постоянный тепловой поток с установленной постоянной температурой. Тепловой поток на выходе обогревателя определяется следующим выражением:
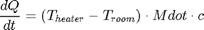
| (2.9) |
где  - тепловой поток,
- тепловой поток,
с-тепло емкость воздуха, Дж/К;
Mdot – заданный поток воздуха, кг/час;
Theater – температура на выходе обогревателя;
Эмитационная модель в Similink выглядит, как это показано на рисунке ниже. При этом вход системы on/off определяется выходом регулятора температуры и принимает значение 0 или 1.
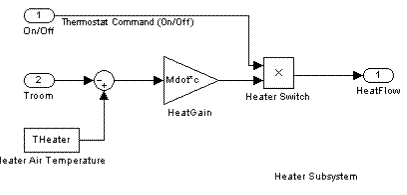
Рисунок 2.5
Регулятор заданной температуры
В качестве регулятора температуры используется модель термостата, которая реализуется на блоке реле. Подсистема термостата изображена на рисунке ниже:
"

Рисунок 2.6 Внутренняя структура подсистемы термостата
Параметры реле устанавливаются следующим образом, как это показано на рисунке ниже. При этом Switch on point, Switch off point – точки включения и выключения реле. Output when on, Output when off – значения на выходе реле при влюченном и выключенном состоянии.

Рисунок 2.7 Установка параметров реле.
На вход регулятора поступает разница текущей температуры помещения и заданной.

Рисунок 2.8 Прдсистема термостата в общей моделе
Модель окружающей среды
При моделировании окружающей среды интересует температура воздуха вне помещения, здания. Данный параметр можно промоделировать от времени, как функцию sin. При этом параметры синусойды соотетствуют функции 15+5*sin(2*Pi/24), т.е. в течении суток изменение температуры будет происходить от 10 до 20 градусов.

Рисунок 2.9 Система моделирования окружающей среды
Имея данные статистики и соответсвующую аппроксимирующую функцию можно моделировать изменения температуры за год. В таблице ниже приведены данные измерения температуры окружающего воздуха в центральной части России за период с 1992 по 2011 года
|
|
|
.
Таблица 3 Статистика измерения темпартуры
| СНиП | среднее | ||||||||||||||
| январь | -10,2 | -4,2 | -5,4 | -4,0 | -3,9 | -6,8 | -6,6 | -3,1 | -11,2 | -1,6 | -5,7 | -5,5 | -14,5 | -7,6 | -6,2 |
| февраль | -9,2 | -5,1 | -1,9 | -7,3 | 0,0 | -8,5 | -7,0 | -8,9 | -12,9 | -11,0 | -1,7 | -5,4 | -8,4 | -11,1 | -6,9 |
| март | -4,3 | -0,2 | -0,5 | -1,9 | 2,3 | -2,8 | 1,3 | -5,7 | -3,4 | 4,8 | 2,0 | -0,5 | -0,9 | -1,9 | -0,6 |
| апрель | 4,4 | 9,8 | 11,4 | 11,2 | 7,7 | 4,9 | 4,8 | 7,5 | 6,1 | 6,1 | 9,8 | 5,3 | 8,5 | 6,7 | 7,7 |
| май | 11,9 | 9,0 | 11,2 | 11,3 | 12,6 | 15,5 | 11,7 | 15,1 | 12,7 | 16,5 | 11,4 | 13,8 | 16,9 | 14,8 | 13,3 |
| июнь | 16,0 | 21,9 | 16,3 | 16,5 | 17,4 | 12,8 | 14,9 | 16,6 | 18,4 | 17,4 | 16,0 | 17,4 | 18,9 | 19,2 | 17,2 |
| июль | 18,1 | 21,6 | 19,4 | 23,1 | 22,8 | 20,7 | 19,3 | 19,4 | 18,3 | 19,1 | 19,3 | 19,3 | 26,2 | 23,5 | 20,9 |
| август | 16,3 | 16,4 | 16,6 | 16,9 | 16,9 | 17,0 | 18,3 | 17,4 | 17,8 | 20,3 | 17,7 | 15,7 | 21,9 | 18,8 | 17,8 |
| сентябрь | 10,7 | 11,8 | 9,8 | 12,1 | 11,6 | 11,2 | 11,9 | 13,1 | 13,3 | 12,0 | 10,9 | 13,9 | 11,7 | 12,1 | 12,0 |
| октябрь | 4,3 | 7,3 | 7,0 | 4,8 | 2,3 | 5,3 | 5,8 | 5,8 | 7,2 | 6,8 | 9,0 | 5,8 | 3,9 | 6,9 | 6,0 |
| ноябрь | -1,9 | -4,5 | -0,3 | -0,5 | -1,7 | 1,1 | -1,8 | 1,4 | 0,7 | -2,3 | 2,1 | 2,3 | 2,7 | 0,2 | 0,0 |
| декабрь | -7,3 | -1,3 | -2,4 | -10,6 | -12,1 | -2,0 | -2,6 | -4,3 | 1,1 | -1,8 | -1,9 | -6,7 | -7,6 | -0,2 | -4,0 |
Аппроксимацию данных можно провести, применяя инструмент Curve Fitting Tool, которая доступна в стандартных инструментах Matlab. Для этого необходимо создать две переменных X и T. В переменную X поместить номера месяцев через выполнение следующих команд в командной строке (комментарии после % не вводить):
T=[];% создать переменную для температур
X=[1:12]’;%В результате будет создан массив данных.
% Моделирование производится по неделям, поэтому необходимо данную переменную домножить на 4:
X=X*4;
%Далее необходимо в переменную Т внести данные по температуре за каждый месяц. Это можно сделать скопировав данные за заданный год в переменную через Workspace и ArrayEditor следующим образом:

Рисунок 2.10 Воод данных за 2011 год
Теперь подготовленный массив данных необходимо аппроксимировать. Для это го выполняется команда
|
|
|
cftool(X,T)
Далее в появившемся окне необходимо выбрать опцию Fitting. В силу периодичности изменения температуры для аппроксимации данных хорошо подходит тип функций суммы синусойд, как это показано на рисунке ниже.

Рисунок 2.11 Аппроксимация данных заданной функцией
Далее необходимо нажать кнопку Apply и в окне Results появятся данные аппроксимации для функции a1*sin(b1*x+c1)+ a2*sin(b2*x+c2):
a1 = 13.77
b1 = 0.1516
c1 = -2.475
a2 = 333.7
b2 = 0.0006401
c2 = 0.009151
Теперь полученные данные необхоимо вставить в подмодель окружающей среды в Simulink. Для этого необходимо добавить два блока Sin соединенных сумматором:
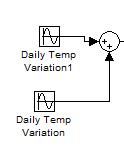
Рисунок 2.12 Схема моделирования температуры окружающей среды
В каждом блоке необходимо выставить полученные коэффициенты, как это показано на рисунке ниже

Рисунок 2.13 Установка параметров для первой синусойды
Аналогичным образом необходимо выставить параметры для второй синусойды.
Далее необходимо добавить в модель возможность изменения температуры в течении одной недели от заданной величины по случайному закону. Для упрощения можно считать, что данные изменения являюся аддитивными относительно заданной температуры и моделируются по нормальному закону распределения N (mX, D) с нулевым математическим ожиданиям (mX=0) и заданной дисперсией D. Для расчета дисперсии D при заданном отклонении температуры (deltaT) можно воспользоваться тем, что при нормальном законе распределения 98% всех случайных величин попадают в промежуток ±3σ, где σ =  . Таким образом
. Таким образом
D= σ2= (deltaT /3)2
Для моделирования колебания температуры необходимо добавить блок датчик случайных чисел (Random Number) и установить параметр mean=0, variance =D.
Общая схема омодели кружающей среды выглядит следующим образом:

Рисунок 2.14 Подмодель окружающей среды
При deltaT=3 C для данных 2011 годав результате моделирования получится следующая зависимость температуры от номера недели:

Рисунок 2.15 Моделирование температуры окружающей среды
Общая модель
Общая модель будет содержать все подмодели, соединенные по следующей схеме.

Рисунок 2.16 Общая модель
Как можно видеть на выходе из подмодели обогревателя (Heater) стоит интегрирующее звено, выход которого будет формировать величину расхода электроэнергии. Перемножение данного блока на тарифную стоимость даст расход электроэнергии в денежном эквиваленте в заданный момент моделирования.
|
|
|
В результате моделирования при заданных параметрах (2011 год, тариф соответсвует 1 руб/кВт*ч) на выходе получатся следующие графики:

Рисунок 2.17 Результат моделирования в течении года
Общий расход за электроэнергию составил 5.12*104 рублей за весь год работы.
Для моделирования в течении двух суток необходимо пересчитать коэффициенты. Температуру окружающей среды можно представить как синусойду. При ширине гестерезиса 4 градуса в результате моделирования получится следующая картина:

Рисунок 2.18 Результат моделирования в течении 2-х суток
|
|
|


