 |
Прохождение света через турмалин (опыт)
|
|
|
|
РИС.25-1
Поляризация электромагнитной волны
Если в среднем по времени вектор  (или
(или  ) расположен вполне симметрично относительно направления распространения волны, то электромагнитная волна называется неполяризованной, или естественной волной.
) расположен вполне симметрично относительно направления распространения волны, то электромагнитная волна называется неполяризованной, или естественной волной.
Усреднение по времени, много большем периода волны.
 |
Поляризацией электромагнитной волны (или любой поперечной волны) называется нарушение осевой симметрии смещений относительно направления распространения волны.
РИС.25-2
Причины возникновения поляризации:
- отсутствие осевой симметрии в излучателе;
- распространение волны в анизотропной среде;
- преломление и отражение волн на границе раздела.
Предельно асимметричный случай – плоско-поляризованная волна.
Наиболее общий случай поляризации = эллиптическая, когда конец вектора  (или ортогонального ему вектора
(или ортогонального ему вектора  ) движется по эллипсу; ее частный случай – циркулярная поляризация.
) движется по эллипсу; ее частный случай – циркулярная поляризация.
Поток энергии в электромагнитной волне
Энергия электростатического поля в диэлектрике:
 .
.
Энергия магнитного статического поля в магнетике:
 .
.
Поскольку в электромагнитной волне, распространяющейся в среде с  и
и  , имеется и электрическое (переменное), и магнитное (переменное) поле, то естественным обобщением можно записать:
, имеется и электрическое (переменное), и магнитное (переменное) поле, то естественным обобщением можно записать:
 .
.
Электромагнитные волны не даны нам в ощущении, об их существовании мы можем судить лишь по действию электромагнитного поля, например, по механическому (давление света, в частности) или по тепловому эффекту.
Рассмотрим изменение во времени количества энергии  , находящегося внутри объема
, находящегося внутри объема  , ограниченного поверхностью
, ограниченного поверхностью  . Цель этой работы – изучение законов сохранения энергии электромагнитного поля, разработка методов экспериментальной проверки уравнений Максвелла.
. Цель этой работы – изучение законов сохранения энергии электромагнитного поля, разработка методов экспериментальной проверки уравнений Максвелла.
|
|
|
Итак,

Рассматриваем подынтегральную функцию.
Предполагаем. что 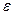 и
и  не зависят от времени, поэтому:
не зависят от времени, поэтому:
 .
.
 и
и  берем из уравнений Максвелла:
берем из уравнений Максвелла:
 , отсюда
, отсюда 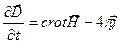 ;
;
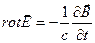 , отсюда
, отсюда  .
.
Подставляем:
 .
.
Математическое отступление:
 .
.
Следовательно,
 .
.
Окончательный вид подынтегральной функции:
 .
.
Изменение энергии электромагнитной волны во времени:
 =
=
{второй интеграл преобразуем по теореме Гаусса из векторного анализа}=
 .
.
Если поверхность  охватывает область полного заряда
охватывает область полного заряда 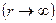 , то
, то
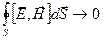 , так как
, так как  .
.
Поэтому:  .
.
Если все находящиеся в электромагнитном поле тела неподвижны, то энергия электромагнитного поля расходуется только на работу электрического поля над токами проводимости.
Если среда непроводящая (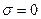 - надо заметить, что на всех частотах!), то в области полного поля энергия электромагнитного поля сохраняется:
- надо заметить, что на всех частотах!), то в области полного поля энергия электромагнитного поля сохраняется:
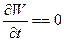 .
.
Вектор Умова-Пойнтинга
Если  не охватывает область полного поля, то
не охватывает область полного поля, то  , и уравнение баланса энергии есть
, и уравнение баланса энергии есть
 .
.
Введем вектор  - вектор Умова-Пойнтинга.
- вектор Умова-Пойнтинга.
 (
( - направление распространения волны).
- направление распространения волны).
Теперь:
 - закон сохранения энергии.
- закон сохранения энергии.
В каждой точке поля плотность потока электромагнитной энергии, то есть количество энергии, протекающей через единицу поверхности ( направлению потока) в единицу времени, равна по величине и направлению вектору
направлению потока) в единицу времени, равна по величине и направлению вектору  .
.
Запишем закон сохранения энергии электромагнитного поля в непроводящей среде
 ,
,
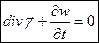 - уравнение непрерывности для плотности потока энергии электромагнитного поля.
- уравнение непрерывности для плотности потока энергии электромагнитного поля.
Поток энергии в плоской волне
 .
.
Поток  совпадает с направлением распространения электромагнитной волны и движется с той же скоростью, что и волна.
совпадает с направлением распространения электромагнитной волны и движется с той же скоростью, что и волна.
Диапазон существования электромагнитных волн:
-  расстояний, доступных эксперименту, отличающему их от электро- или магнитостатической волны;
расстояний, доступных эксперименту, отличающему их от электро- или магнитостатической волны;  ~107см;
~107см;
|
|
|
-  ~10-13см – минимальное расстояние в теории элементарных частиц:
~10-13см – минимальное расстояние в теории элементарных частиц:  с (квант времени?).
с (квант времени?).
 см
см
Оптика – раздел физики, изучающий законы распространения электромагнитных волн в различных средах и их взаимодействие с материей.
Широкое практическое применение оптики:
- светотехника,
- техническая оптика,
- физиологическая оптика,
- оптоэлектроника и т.д.
Три подхода:
- волновая оптика (этим, в основном, мы будем заниматься);
- корпускулярная оптика (кванты с энергией  - дуализм «волна-частица»);
- дуализм «волна-частица»);
- геометрическая оптика основана на понятии луча и не затрагивает микроскопических проблем взаимодействия излучения с веществом; она оперирует макроскопическими характеристиками вещества ( ) и использует геометрические аксиомы и постулаты.
) и использует геометрические аксиомы и постулаты.
Основные понятия
Плоская волна,  распространяющаяся по направлению оси
распространяющаяся по направлению оси 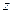 :
:


или  .
.
Реализовать плоскую волну можно с помощью коллиматоров – линзовых и зеркальных:

РИС.25-3
Фронт волны тем более плоский, чем меньше расходимость пучка. У газовых лазеров расходимость  ~
~  , но с помощью специальных коллиматоров можно уменьшить расходимость до
, но с помощью специальных коллиматоров можно уменьшить расходимость до  .
.
 |
Понятие монохроматической волны идеализировано. Монохроматическая волна рождается колебанием, которое длится вечно.
РИС.25-4
На самом деле в некий момент времени  колебание начинается, а в момент времени
колебание начинается, а в момент времени  колебание заканчивается. В идеальном варианте
колебание заканчивается. В идеальном варианте  . На самом деле
. На самом деле  , где
, где  - период колебаний, значит, излучение не является монохроматическим в строгом смысле. Оно представляет собой импульс излучения конечной длительности
- период колебаний, значит, излучение не является монохроматическим в строгом смысле. Оно представляет собой импульс излучения конечной длительности  . Такой импульс, как известно, может быть разложен в ряд Фурье, то есть может быть представлен в виде суммы конечного или бесконечного числа членов вида
. Такой импульс, как известно, может быть разложен в ряд Фурье, то есть может быть представлен в виде суммы конечного или бесконечного числа членов вида  . Чем меньше длительность импульса, тем шире спектр содержащихся в нем частот
. Чем меньше длительность импульса, тем шире спектр содержащихся в нем частот  .
.
Какова природа излучения? Кратко и схематично – это световые кванты, излучаемые отдельными атомами при электронных переходах. Поэтому фактически каждый акт излучения происходит в течение времени  . Отсюда следует, что в спектрах нагретых тел (и, конечно в дневном свете Солнца) содержатся все частоты от 0 до
. Отсюда следует, что в спектрах нагретых тел (и, конечно в дневном свете Солнца) содержатся все частоты от 0 до  , и нужно предпринять вполне определенные усилия, чтобы выделить составляющие с определенной частотой
, и нужно предпринять вполне определенные усилия, чтобы выделить составляющие с определенной частотой 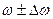 (или с определенной длиной волны
(или с определенной длиной волны  ).
).
|
|
|
Для выделения определенной частоты, определенной длины волны из так называемого «белого» света (из сплошного спектра частот) служат различные устройства, называемые монохроматорами. Главная часть монохроматора – это устройство (среда, элемент), свойства которого сильно зависят от длины волны. Как правило, выбор того или иного способа выделения монохроматического излучения и, следовательно, ширина выделяемого интервала частот  задаются условиями задачи.
задаются условиями задачи.
Чаще всего используются:
 |
фильтр – от частоты зависит прозрачность (
 велико), призма – от частоты зависит угол отклонения луча света (
велико), призма – от частоты зависит угол отклонения луча света ( меньше, чем у фильтра), решетка дифракционная – от частоты зависят и угол отклонения и другие оптические характеристики; употребляется, как правило, в сочетании с фильтром (
меньше, чем у фильтра), решетка дифракционная – от частоты зависят и угол отклонения и другие оптические характеристики; употребляется, как правило, в сочетании с фильтром ( мало).
мало).
РИС.25-5
Наиболее монохроматичное излучение получается с помощью лазеров:
He-Ne - 6328 Å, CO2 – 10.6 мкм, АИГ(алюмо-иттриевый гранат):Nd – 1.06 мкм.
Поляризация излучения
В естественном свете встречаются все возможные поляризации, и это обусловлено природой каждого элементарного акта излучения: один излучатель работает  с, поэтому все направления колебаний электрического вектора электромагнитной волны оказываются равновероятными. В естественном свете смешаны электромагнитные колебания всевозможных поляризаций. Чтобы выделить колебания с определенной поляризацией, используются устройства, называемые поляризаторами.
с, поэтому все направления колебаний электрического вектора электромагнитной волны оказываются равновероятными. В естественном свете смешаны электромагнитные колебания всевозможных поляризаций. Чтобы выделить колебания с определенной поляризацией, используются устройства, называемые поляризаторами.
Исторически – впервые явление раздваивания луча при прохождении через кристалл исландского шпата было открыто Бартолином в 1670 г. Через 20 лет, в 1690 г., Гюйгенс обнаружил, что эти лучи ведут себя по-разному при прохождении через второй кристалл исландского шпата - интенсивность одного из лучей падает до нуля.
Чтобы понять эти явления, необходимы представления о симметрии кристаллов.
Имеются 32 различные точечные группы симметрии (7 кристаллических классов), с учетом трансляционной симметрии получаются 230 пространственных групп.
|
|
|
Принцип Неймана
Элементы симметрии любого физического свойства кристалла должны включать элементы симметрии точечной группы кристалла.
С точки зрения оптических свойств 7 кристаллических классов делятся на:
| Оптически изотропные | Одноосные | Двуосные |
| Кубический кристалл Оптически изотропными являются также аморфные среды | Тетрагональная Тригональная Гексагональная структура | Триклинная Моноклинная Орторомбическая структура |
Прохождение света через турмалин
Турмалин – это минерал сложного состава, тригональная система, точечная группа  : три зеркальные плоскости симметрии под углом
: три зеркальные плоскости симметрии под углом  . Турмалин – оптически одноосный кристалл.
. Турмалин – оптически одноосный кристалл.
 |
РИС.25-6
 |
РИС.25-7
Ось третьего порядка – это оптическая ось кристалла турмалина.
 - направление распространения электромагнитных волн перпендикулярно оптической оси.
- направление распространения электромагнитных волн перпендикулярно оптической оси.
Если пластину вращать, то интенсивность света не меняется.
Поставим вторую пластинку турмалина:
 |
РИС.25-8
Интенсивность света, прошедшего через пластинки, зависит от угла между осями  , причем интенсивность
, причем интенсивность  , где
, где  .
.
Объяснение:
1) Какова интенсивность излучения, прошедшего через пластинку 1.
 |
Пусть в некоторый момент времени на пластинку падает электромагнитная волна, такая, что электрический вектор в этой волне составляет угол

 с оптической осью
с оптической осью  .
.
РИС.25-9
Параллельная оси  компонента электрического вектора:
компонента электрического вектора: 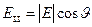 .
.
Перпендикулярная компонента электрического вектора:  - не проходит.
- не проходит.
Интенсивность прошедшего излучения:  .
.
Это интенсивность, определяемая углом между направлением электрического вектора и осью  . В падающем излучении присутствуют все возможные направления электрического вектора. Поэтому для вычисления интенсивности прошедшего через пластинку света необходимо провести усреднение по всем направлениям, т.е. по всем углам
. В падающем излучении присутствуют все возможные направления электрического вектора. Поэтому для вычисления интенсивности прошедшего через пластинку света необходимо провести усреднение по всем направлениям, т.е. по всем углам  .
.
Интенсивность падающей на пластинку волны:  .
.
Интенсивность прошедшей волны:
 {
{  от угла не зависит} =
от угла не зависит} =  =
= 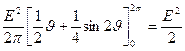 .
.
 |
Интенсивность света, прошедшего через одноосную пластинку не зависит от угла и составляет ровно 50% от интенсивности падающего света.
РИС.25-10
Через вторую пластинку пройдет  - закон Малюса.
- закон Малюса.
Значит, если  , где
, где  - любое целое число, (перпендикулярная установка поляризатора), то
- любое целое число, (перпендикулярная установка поляризатора), то  .
.
Если  (параллельная установка), то
(параллельная установка), то  - проходит все излучение, падающее на вторую пластинку.
- проходит все излучение, падающее на вторую пластинку.
Степень поляризации:  .
.
Исследуется зависимость интенсивности излучения, прошедшего через вторую пластинку от угла  между оптическими осями этих пластинок.
между оптическими осями этих пластинок.
|
|
|
Для естественного света вращение одной пластинки не изменяет интенсивности прошедшего света (здесь и используется только одна пластинка).
Следовательно, здесь  и
и  .
.
Прошедший через первую пластинку свет является плоско поляризованным, тогда через вторую пластинку ничего не пройдет при  , следовательно,
, следовательно,  - второй предельный случай.
- второй предельный случай.
Степень (коэффициент поляризации меняется от 0 для естественного света до 1 для плоско поляризованного света. Во всех остальных случаях  .
.
Имеются и иные методы создания излучения, поляризованного определенным образом (кроме рассмотренного случая поляризации при прохождении через одноосные кристаллы), например, поляризация при отражении (при падении света на зеркало под определенным углом). Однако из изложенного следует, что для создания плоской монохроматической электромагнитной волны нужно воспользоваться коллиматором, монохроматором и поляризатором.
Часто используется представление о квазимонохроматической волне 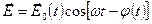 , где
, где  и
и  - медленно меняющиеся функции времени. Вы убедились в возможности практической реализации плоской волны и в невозможности реализации монохроматической волны. Обратим внимание на несколько важных моментов.
- медленно меняющиеся функции времени. Вы убедились в возможности практической реализации плоской волны и в невозможности реализации монохроматической волны. Обратим внимание на несколько важных моментов.
Монохроматическая волна – бесконечная в пространстве – создается гармоническими колебаниями, бесконечными во времени. Реальные колебания продолжаются некоторое конечное время  . Вы знаете, что немонохроматичность волны обуславливает конечную ширину спектральной линии. Существенным является связь между длительностью гармонического колебания и шириной спектральной линии. Путем разложения цуга волн в интеграл Фурье получили:
. Вы знаете, что немонохроматичность волны обуславливает конечную ширину спектральной линии. Существенным является связь между длительностью гармонического колебания и шириной спектральной линии. Путем разложения цуга волн в интеграл Фурье получили:
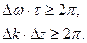
[26] Скорости волнового движения
Отдельные осцилляторы, составляющие среду, не перемещаются, а лишь колеблются около своих положений равновесия; мы наблюдаем как волны лишь фазовые соотношения между отдельными осцилляторами.
Три скорости.
1) Скорость частиц:
 - обычная гармоническая скорость.
- обычная гармоническая скорость.
2) Фазовая скорость – скорость перемещения по оси 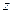 поверхности постоянной фазы:
поверхности постоянной фазы:

3) Групповая скорость  – скорость распространения информации в волне. Если волна информации не переносит, то
– скорость распространения информации в волне. Если волна информации не переносит, то  . Например –монохроматическая волна.
. Например –монохроматическая волна.
Чтобы волна переносила информацию, ее надо как-то пометить (промодулировать).



 ,
,  - несущая частота,
- несущая частота,  - частота модуляции.
- частота модуляции.
В результате излучения возникает волна, содержащая частоты в диапазоне  .
.
 Гц.
Гц.

РИС.26-1
Для передачи информации нужен некоторый интервал частот.
По мере уменьшения полосы частот убывает и объем передаваемой информации. Как только  , информация
, информация  . Монохроматическая волна информации не несет.
. Монохроматическая волна информации не несет.
Информация передается группой волн.
Информация не может распространяться со скоростью  , иначе будет нарушен принцип причинности:
, иначе будет нарушен принцип причинности:  .
.
Информация передается с помощью модуляции, значит, групповая скорость определяется скоростью распространения фазы модуляции:
 .
.
Приращение фазы:  ,
,
 - разность значений функций, деленная на разность значений аргументов.
- разность значений функций, деленная на разность значений аргументов.
Вспомним ряд Тейлора:

Отсюда находим:

При достаточной малости интервала 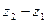 :
:
 .
.
Отсюда – групповая скорость:  .
.
Фазовая:  .
.
Примеры
1. Вакуум  (среда без дисперсии).
(среда без дисперсии).
 ;
;  ;
;  .
.
Примечание. Дисперсия света открыта Ньютоном в 1672 г. Разложение света в спектр происходит потому, что показатель преломления вещества зависит от частоты (или от длины волны) º фазовая скорость зависит от частоты:  .
.
Нормальная дисперсия:  ,
,  .
.
Аномальная дисперсия:  ,
,  .
.

РИС.26-2
2. Электронная плазма
 , где
, где 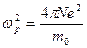 ,
,  - собственная частота колебаний всего коллектива электронов как целого.
- собственная частота колебаний всего коллектива электронов как целого.
Фазовая скорость в плазме:  .
.
Групповая скорость в плазме: 
 Þ
Þ  Þ
Þ  .
.
Отсюда:  .
.
Связь между групповой и фазовой скоростями
 .
.
С учетом  ,
, 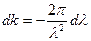 :
:
 - формула Релея.
- формула Релея.
Если имеется среда с нормальной дисперсией, то есть  , то
, то  .
.
Если среда с аномальной дисперсией, то  , то
, то  .
.
Аномальная дисперсия наблюдается только в области сильного поглощения, где электромагнитная волна распространяется на расстояние порядка  и понятие
и понятие  становится бессмысленным.
становится бессмысленным.
Замечания
- Всегда в эксперименте определяется
 . Фазовая скорость
. Фазовая скорость  непосредственно не измеряется и определяется как
непосредственно не измеряется и определяется как  .
. - Полезная формула:
 .
.
Стоячие электромагнитные волны
 |
РИС.26-3
В свободной волне  и
и  синфазны.
синфазны.
Ранее мы получали решение волнового уравнения в виде двух плоских волн, распространяющихся навстречу друг другу:
 |
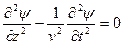 Þ
Þ 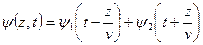 (первое слагаемое – распространение волны в положительное направление
(первое слагаемое – распространение волны в положительное направление 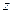 , второе – в отрицательное направление
, второе – в отрицательное направление 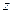 ). Реально такие волны возникают в результате отражений электромагнитных волн от границ той области, в которой они распространяются.
). Реально такие волны возникают в результате отражений электромагнитных волн от границ той области, в которой они распространяются.
РИС.26-3
Падающая волна:  .
.
Отраженная волна:  Þ необходимым условием отражения является изменение фазы
Þ необходимым условием отражения является изменение фазы  или
или  на
на  .
.
Если  , то меняется фаза
, то меняется фаза  (как на рисунке), а
(как на рисунке), а  синфазны.
синфазны.
Определим величину вектора  , получающегося в результате взаимодействия падающей и отраженной волн:
, получающегося в результате взаимодействия падающей и отраженной волн:  .
.
 ,
,
 ,
,


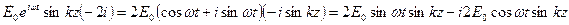 .
.
 ;
;
 (если
(если  , то появляется еще множитель
, то появляется еще множитель  ).
).
При отражении от оптически более плотной среды возникает стоячая волна:
 ;
;  .
.
Это стоячие волны. Фазы  и
и  сдвинуты на
сдвинуты на  .
.

РИС.26-4
Вектор Пойнтинга обращается в нуль каждую  . Переноса энергии в стоячей волне нет.
. Переноса энергии в стоячей волне нет.
Проверка справедливости развитых представлений была осуществлена:
для метровых волн Г. Герцем, для световых волн О. Винером в 1892 г. – исследования стоячих световых волн в толстослойных фотопластинках.
Измерение скорости света с помощью стоячих волн
Стоячие электромагнитные волны:
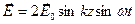 ,
,
 .
.

РИС.26-5
 ;
;  задается генератором и измеряется с высокой точностью,
задается генератором и измеряется с высокой точностью,  измеряется в волноводе, расчет дает
измеряется в волноводе, расчет дает  .
.
Исследования стоячих световых волн в толстослойных фотопластинках (О. Винер,1892 г.)
 5000Å/5×10-4=5×10-5см/5×10-4=10-1см~1мм – наблюдаемая величина.
5000Å/5×10-4=5×10-5см/5×10-4=10-1см~1мм – наблюдаемая величина.
Первое почернение – на  , то есть ответственным за фотохимическое действие является вектор
, то есть ответственным за фотохимическое действие является вектор  .
.
Объяснение:
Электромагнитное поле воздействует на заряды:  ; так как
; так как  , то второй член, как правило, пренебрежимо мал.
, то второй член, как правило, пренебрежимо мал.
 |
РИС.26-6
Цветная фотография по способу Г. Липпмана (Нобелевская премия 1908 г.).
 |
Устанавливаются стоячие волны, слои
 соответствующего цвета. Если осветить пластинку белым светом, то в отраженном свете будут присутствовать волны с длиной волны, соответствующей решетке в данном месте.
соответствующего цвета. Если осветить пластинку белым светом, то в отраженном свете будут присутствовать волны с длиной волны, соответствующей решетке в данном месте.
РИС.26-7
Отражение и преломление электромагнитных волн на границах раздела
В однородной среде ( ) электромагнитные волны распространяются прямолинейно и не затухают, если электропроводность
) электромагнитные волны распространяются прямолинейно и не затухают, если электропроводность  . При наличии неоднородностей электромагнитная волна отражается, преломляется, рассеивается.
. При наличии неоднородностей электромагнитная волна отражается, преломляется, рассеивается.
Простейший случай: резкая граница раздела двух диэлектриков (заряд на поверхности, ток по поверхности равны нулю). Нормальное падение.
 |
РИС.26-8
Условие на границе раздела:  ,
,  .
.
Падает на границу плоско поляризованная монохроматическая волна:
 ,
,
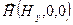 ,
,
 .
.
Падающая волна:  ,
,
 ,
,
 .
.
Отраженная волна:  ,
,
 ,
,
 .
.
Преломленная (прошедшая) волна:  ,
,
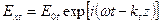 ,
,
 .
.
Из условия непрерывности тангенциальных компонент на границе раздела следует:
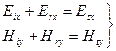 - сюда подставляем выражения для волн.
- сюда подставляем выражения для волн.
Получаем:
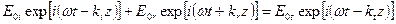 ;
;
 .
.
Полученная система должна удовлетворяться при любых 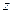 , в том числе при
, в том числе при  .
.
Отсюда:
 ;
;
 .
.
Сокращая на 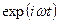 - поскольку система должна удовлетворяться во все моменты времени, имеем:
- поскольку система должна удовлетворяться во все моменты времени, имеем:
 .
.
Делим (2) на (1):
 .
.
Отсюда легко вычислить связь амплитуд отраженной и падающей волн:
 ,
,
 ,
,
 Þ Фазовые соотношения:
Þ Фазовые соотношения:  {signºзнак}.
{signºзнак}.
Амплитудный коэффициент отражения:
 .
.
Энергетический коэффициент отражения равен отношению среднего потока энергии в отраженной волне к среднему потоку энергии в падающей волне:
 .
.
На опыте измеряется энергетический коэффициент отражения, поскольку все приемники реагируют на интенсивность волны, то есть на квадрат ее амплитуды.
Примеры:
1) Стекло-воздух:  ;
;  .
.
2) Германий-воздух:  ;
;  .
.
1930  при
при  (металлы).
(металлы).
27 Прошедшая (преломленная) волна
Берем все ту же систему уравнений:
 .
.
Делим второе уравнение на  :
:
 (2).
(2).
Складываем второе с первым:
 ,
,
 .
.
Амплитудный коэффициент прозрачности:
 Þ Фазовые соотношения:
Þ Фазовые соотношения:  и
и  всегда синфазны.
всегда синфазны.
Энергетический коэффициент прозрачности равен отношению среднего потока энергии в прошедшей волне к среднему потоку энергии в падающей волне:
 .
.
Соотношение между коэффициентами
Из закона сохранения энергии:
 .
.
Поделив правую и левую части на среднее значение энергии в падающей волне  , имеем:
, имеем:  .
.
Проверим:
 .
.
Измерения коэффициентов отражения и прозрачности
Абсолютные:
 |
РИС.27-1
Относительные:

РИС.27-2
О просветлении оптики
При отражении от двух границ стекло-воздух теряется чуть меньше 8% энергии.
 |
РИС.27-3
В объективах высокого разрешения имеется 6-10 различных оптических стекол (у которых показатель преломления


