 |
Моделирование ИС с помощью сетей Петри. Выполнение сети Петри, анализ достижимости маркировки
|
|
|
|
Сети петри используются для анализа взаимосвязи вычислительных процессов.
Первоначально сети петри использовались для описания взаимодействия аппаратуры различного назначения: позже выяснилось, что сети петри позволяют анализировать
Сети петри позволяют представлять и изучать динамики поведения системы параллельных процессов в программе или в любом другом исследуемом устройстве.
Сети петри состоят из 4 элементов
- множество позиций Pi
- Множество переходов T
- Входная деформация I
- Выходная деформация O
Практически удобно изображать сети петри в виде графа
Применительно к вычислительной системе планки соответствуют вычислительным процессам а позиции – данным, событиям или условиям
Разметка сети
Маркировка сети петри представляет собой присвоение фишек позициям сети. Процесс перераспределения фишек в сети называется выполнением сети петри. Фишки находятся на входных позициях перехода и управляют запуском перехода в сети. Переход запускается удалением фишек из всех его входных позиций и образованием новых фишек помещаемых во все выходные позиции.
Введем понятие вектора маркировки. Число элементов в векторе равно числу позиций. Извлечения элементов вектора отображают количество фишек в позиции.
Одной из центральных задач описываемых сетью петри является задача определения достижимости маркировки когда до исходного вектора маркировки М0 требуется установить существование последовательности переходов после которых достигается некоторый заданный входной вектор маркировки М1.
Анализ достижимости заключается в следующем: структура сети описывается двумя матрицами D’ и D’’
Матрица входа D’
|
|
|
Количество строк = количество переходов
А количество столбцов равно числу позиций.
Входная матрица отражает структуру связи позиции со входами переходов
Выходная матрица D’’
Отражает соединение переходов с позициями
Вектор запусков переходов X=(x1,x2,x3,x4)
Число элементов в данном векторе равняется количеству переходов
Значение каждого элемента определяет количество запусков перехода но не их последовательность.
m1 = m0 + X(D’’-D’)
если уравнение истинно то задача достижимости решаема
19. Сетевое планирование
Сетевой график
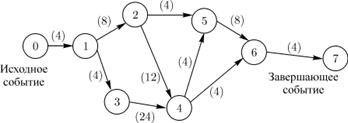
Всякий намеченный комплекс работ, необходимых для достижения некоторой цели, называют проектом. Проект (или комплекс работ) подразделяется на отдельные работы. Каждая отдельная работа, входящая в комплекс (проект), требует затрат времени. Некоторые работы могут выполняться только в определенном порядке. При выполнении комплекса работ всегда можно выделить ряд событий, то есть итогов какой-то деятельности, позволяющих приступить к выполнению следующих работ. Если каждому событию поставить в соответствие вершину графа, а каждой работе — ориентированное ребро, то получится некоторый граф. Он будет отражать последовательность выполнения отдельных работ и наступление событий в едином комплексе. Если над ребрами проставить время, необходимое для завершения соответствующей работы, то получится сеть. Изображение такой сети называют сетевым графиком. Сетевой график состоит из двух типов основных элементов: работ и событий. Работа представляет собой выполнение некоторого мероприятия (например, погрузка боезапаса или переход корабля в пункт базирования). Этот элемент сетевого графика связан с затратой времен и расходом ресурсов. Поэтому работа всегда имеет начало и конец. Кроме того, каждая работа должна иметь определение, раскрывающее ее содержание (например, уяснение боевой задачи, приготовление корабля к походу и т.д.).
|
|
|
На сетевом графике работа изображается стрелкой, над которой проставляется ее продолжительность или затрачиваемые ресурсы, или то и другое одновременно. Работа, отражающая только зависимость одного мероприятия от другого, называется фиктивной работой. Такая работа имеет нулевую продолжительность (или нулевой расход ресурсов) и обозначается пунктирной стрелкой.
Начальная и конечная точки работы, то есть начало и окончание некоторого мероприятия (например, окончание приготовления корабля к бою), называются событиями. Следовательно, событие, в отличие от работы, не является процессом и не сопровождается никакими затратами времени или ресурсов.
Свойства сетевого графика
- ни одно событие не может произойти до тех пор, пока не будут закончены все входящие в него работы.
- ни одна работа, выходящая из данного события, не может начаться до тех пор, пока не произойдет данное событие.
- ни одна последующая работа не может начаться раньше, чем будут закончены все предшествующие ей.
Событие обозначается кружком с цифрой внутри, определяющей его номер.
Работа обычно кодируется номерами событий, между которыми они заключены, то есть парой 
, где 
— номер предшествующего события,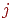 
— номер последующего события.
В одно и то же событие могут входить (выходить) одна или несколько работ. Поэтому свершение события зависит от завершения самой длительной из всех входящих в него работ.
В случае, когда наступление события (например, 3) возможно в результате завершения двух работ 
и 
, но в то же время существует событие 4, зависящее от завершения только одной из этих работ (например, ), вводится фиктивная работа 
.
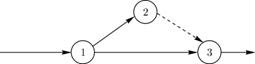
Если одно событие (например, 1) служит началом двух (например, 
и ) или нескольких работ, заканчивающихся в другом событии (3), то для их различия также вводится фиктивная работа 
.
Другое правило построения сетевого графика заключается в том, что если несколько работ может начаться не после полного, а после частичного выполнения определенной работы, то последнюю работу целесообразно представить как сумму ее частей, расчлененных событиям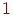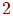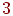и (
, 
, 
, 
и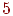 
).
Сетевой график не должен иметь циклов, то есть таких путей, в которых конец последней работы совпадает с началом первой работы. Сетевой график, имеющий хотя бы один цикл, не может быть реализован, так как ни одна из работ, входящих в такой цикл, никогда не может начаться.
|
|
|
Параметры сетевой модели.
· 
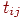— продолжительность -й работы
· наиболее ранее возможное время наступления 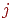-го события, обозначаемое символом 
;
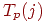· самое позднее допустимое время наступления -го события, обозначаемое символом 
;
· резерв времени данного события, обозначаемый символом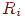 
;
· полный резерв времени работы , обозначаемый символом 
;
· свободный резерв времени работы , обозначаемый символом 
.
· Частичный резерв времени работ r(i,j)
· Частитный резрв времени события r(i)
t(i-j)= 
, где i,j – начальное, конечное время, Q – трудоемкость, А – кол-во исполнителей, f – коэф. Перевода рабочих дней в календарные. f=0.85
Вся последовательность работ в сетевом графике в котором конечное событие предшевствующей работы совпадает с начальным событием последующей называется путем. Продолжительность пути T(L) равна сумме продолжительностей состовляющих его работ.
T(L)= 
|
|
|
