 |
Практическое задание №1 ФОРМАТ А3
|
|
|
|
Цель задания. Закрепление изученного материала на рисование линий, углов,
деление отрезков и углов на равные части и построение рисунков плоских
фигур.
Содержание задания.
1. Рисование линий – горизонтальных, вертикальных и наклонных.
2. Деление отрезков на равные части: 2, 4, 8, 3, 6, 5.
3. Рисование углов: 90◦ и 45◦, 30◦ и 60◦, 7◦ и 41◦.
4. Рисование плоских фигур, таких, как квадрат, пятиугольник, шестиугольник, восьмиугольник, окружность и эллипс.
Краткие методические указания. Лист делят тонкими вертикальными линиями приблизительно на три равные части. Затем первый и третий столбец делят на три равные части двумя горизонтальными прямыми, а средний – на четыре части. В крайнем левом столбце рисуют линии (см. п. 1), ниже показывают деление отрезков, и рисунок углов: 41° и 7°. В следующих вертикальных полях располагают рисунки остальных углов и плоских фигур. Все геометрические тела рисуют примерно одинаковых размеров. Размер стороны квадрата должен быть равен приблизительно 40 - 50 мм.

Практическая работа №2
Построение плоских фигур в аксонометрических проекциях.
Умение строить рисунки плоских фигур дает возможность в дальнейшем рисовать объемные предметы.
Рассмотрим построение рисунков плоских фигур, наиболее часто встречающихся в практике: треугольника, квадрата, шестиугольника и окружности.
Упражнение1. Формат А4.
1. Показать оси прямоугольных аксонометрических проекций, линии штриховки сечений (наносят наносят параллельно одной из диагоналей проекций квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям).
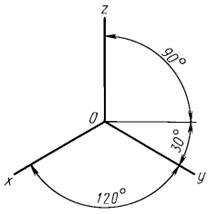
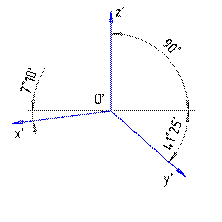

Оси изометрической прямоугольной проекции Оси диметрической прямоугольной проекции
|
|
|
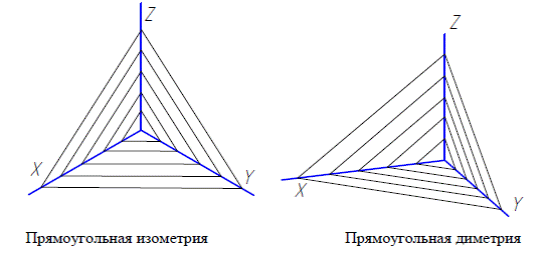
Линии штриховки
Упражнение2. Формат А4.
Постройте проекции плоских фигур в изометрической и диметрической прямоугольной проекции. Размеры сторон фигур 30-40 мм.
Построение треугольника
Пусть требуется построить рисунок прямоугольного треугольника ВАС, у которого две стороны совпадают с аксонометрическими осями (рис. 2.1.а) х, z и нарисовать его в изометрии (рис. 2.1.б) и диметрии (рис. 2.2.в). Проведем две взаимно перпендикулярные прямые (рис. 2.1.а) и отложим от точки А2 отрезки А2В2 и А2С2. Прямая В2С2 будет гипотенузой прямоугольного треугольника В2 А2С2.
Построение треугольника
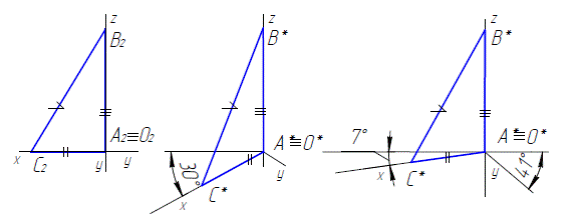
а б в
Рисунок 2.1- Изометрическая проекция диметрическая проекция
Для построения треугольника ВАС в прямоугольной изометрической проекции нарисуем изометрические оси х, y, z (рис. 28), а затем отложим данные отрезки АВ, АС (равные А2В2 и А2С2), на соответствующих осях, точка А* совпадет с точкой О* – точка пересечения аксонометрических осей х, y, z. Стороны АВ и АС треугольника, в данных проекциях откладываются в истинную величину, без искажения. Соединив полученные точки В* и С*, получим аксонометрию треугольника ВАС.
Построения треугольника ВАС в прямоугольной диметрической проекции (рис. 29) выполняются аналогично построениям треугольника ВАС в прямоугольной изометрической проекции.
Построение квадрата
Нарисуем две взаимно перпендикулярные оси (рис. 2.2.а). Точка их пересечения – точка О. От точки О на этих осях отложим отрезки О1, О2, О3, и О4 равные половине стороны квадрата, а затем, через полученные точки,
проведем прямые, параллельные осям. Прежде чем обвести квадрат ярко, необходимо проверить размеры его сторон и углы. Обнаруженные неточности следует исправить, не стирая контуров рисунка. Затем удалить лишние линии ластиком и обвести контур.
|
|
|
Рассмотрим построение квадрата ABCD в прямоугольной изометрии при условии, что его стороны параллельны осям х и y. Нарисуем изометрические оси х и y (рис. 2.2.б) и отложим на них от точки О отрезки О —1, О — 2, О — 3, О—4, равные половине стороны квадрата. Через полученные на осях точки 2 и 4 проведем прямые, параллельные оси х, а через точки 1 и 3, параллельные оси y, которые при пересечении определят вершины ромба ABCD, представляющего собой изображение квадрата в изометрии.
Рисунок квадрата ABCD в прямоугольной диметрии имеет вид параллелограмма, у которого стороны АD и ВС в два раза меньше, чем АВ и CD. Построение его производится в той же последовательности, что и изометрическое изображение (рис. 2.2.в ).
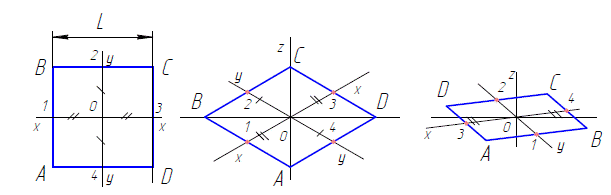
а б в
Рисунок 2.2 - Изометрическая проекция диметрическая проекция
Построение прямоугольника
Начинаем построения с прямого угла. На сторонах угла от его вершины откладываем заданные размеры сторон ав и аd. Через точки в и d проведем прямые, параллельные сторонам прямого угла и проверим точность построения. После исправления ошибок обведем контур рисунка (рис. 2.3.а).
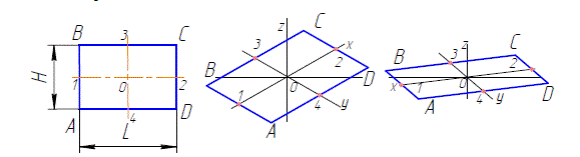
А б в
Рисунок 2.3 - Изометрическая проекция диметрическая проекция
Рисунок прямоугольника в прямоугольной изометрии выполняется следующим образом: Нарисуем оси х и y (рис. 2.3.б). От точки О отложим по оси х отрезки О-1 и О-2, равные половине стороны АD, а по оси y – отрезки О-3 и О-4, равные половине стороны АВ. Через точки 1,2,3,4 проведем прямые, параллельные осям х и y, на пересечении которых получим вершины фигуры – изображения прямоугольника АВСD. На рис. 2.3.в изображен рисунок прямоугольника в прямоугольной диметрии. Стороны ВС и АD нарисованы в истинную величину, а АВ и СD уменьшены в два раза. Таким образом, чертеж прямоугольника в диметрии получился менее выразительным и наглядным, чем в изометрии.
Упражнение3. Формат А4.
Постройте проекции плоских фигур в изометрической и диметрической прямоугольной проекции. Размеры сторон фигур 30-40 мм.
Построение шестиугольника
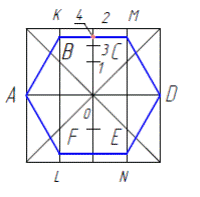
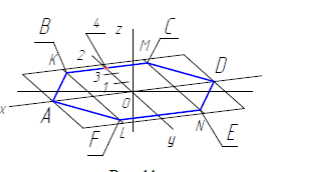
Чтобы нарисовать правильный шестиугольник используют дополнительные построения, таким образом, рисунок получится более точным. Начнем построения с рисунка квадрата в тонких линиях (рис.2.4.а). Через середины соответствующих его сторон проведем две тонкие взаимно перпендикулярные прямые, пересекающиеся в точке О. Горизонтальная прямая АD будет горизонтальной осью шестиугольника. Далее левую и правую части квадрата разделим пополам вертикальными прямыми KL и MN. Затем разделив верхнюю часть вертикальной оси на две равные части, получим отрезки О—1 = 1 —2. Отрезок 1—2 разделим пополам точкой 3 и, наконец, отрезок 2—3 также разделим пополам точкой 4. Через точку 4 проведем горизонтальную прямую, которая пересечет прямые KL и MN в точках В и С. Соединив прямыми точки А, В и С, D, получим рисунок верхней половины правильного шестиугольника. Затем дорисуем нижнюю половину шестиугольника точно в таком же порядке и получим все вершины шестиугольника ABCDEF. Если шестиугольник лежит в горизонтальной плоскости, то аксонометрические построения производятся на осях х, y и параллельных им линиях.
|
|
|
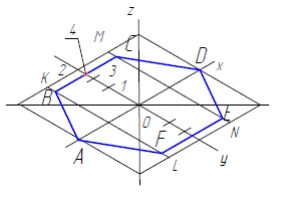
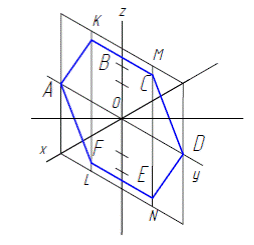
Рисунки шестиугольника ABCDEF в прямоугольной изометрии и прямоугольной диметрии выполним также с помощью дополнительных построений. Нарисуем изометрические оси х, y (рис. 2.4.б ). Построим рисунок квадрата в изометрии (ромб) и проведем в нем прямые KL и MN, параллельно оси y. Определим точки 1, 2, 3, 4 точно в такой же последовательности, в какой они находились при построении рисунка шестиугольника, после чего проведем через точку 4 прямую, параллельную оси х, до пересечения с прямыми KL и MN в точках В и С. Соединив прямыми точки А, В, C и D, получим рисунок половины фигуры шестиугольника. Аналогичным образом нарисуем вторую половину
шестиугольника.
| 
| 
|
| а | б | в |
| 
| |
| г | д | |
| Рисунок 2.4 - | Изометрическая проекция | диметрическая проекция |
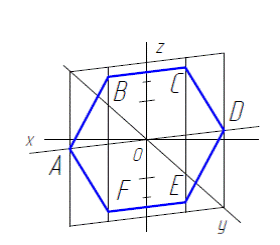
На рис. 2.4.в показано построение шестиугольника ABCDEF в прямоугольной диметрической проекции, аналогично построениям, описанным выше, только по оси y все размеры уменьшаются в два раза. На рис. 2.4.г шестиугольник расположен параллельно профильной плоскости проекций и изображен в прямоугольной изометрии, а на рис. 2.4.д дано построение шестиугольника в прямоугольной диметрической проекции, расположенного параллельно фронтальной плоскости проекций.
|
|
|
Построение окружностей
Рисунок окружности начинается с построения квадрата, в который она вписывается. Это позволяет быстрее получить более правильное изображение окружности.
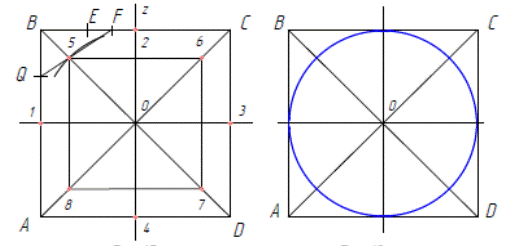
Квадрат ABCD (рис. 2.5.а) начинаем с построения взаимно перпендикулярных линий 1-3 и 2-4, которые являются диаметрами окружности, а потом проводим в нем диагонали АС и BD. Для определения промежуточных точек окружности разделим отрезок В—2 точкой Е пополам. Затем отрезок Е—2 разделим точкой F также пополам. Далее разделим отрезок В—1 на две равные части точкой Q и соединим прямой точку Q с точкой F. Прямая QF пересечет диагональ BD в точке 5. Точка 5 будет удалена от центра квадрата на расстояние радиуса окружности. Через точку 5 проведем горизонтальную и вертикальную прямые до пересечения их с диагональю АС. Получим точки 6 и 8. Точка 7 расположится в нижней половине квадрата симметрично точке 8. Итак, получив все восемь точек, проведем тонкие дуги, которые наметят форму окружности. Чтобы лучше видеть рисунок, нужно отодвинуть его от себя на расстояние вытянутой руки, затем внести изменения, убрать ненужные линии и обвести рисунок (рис. 2.5.б).
а б
Рисунок 2.5 – Построение окружностей
В изометрической проекции окружность изобразится в виде эллипса. Рисунок окружности построим в изометрии. Для этого наметим изометрические оси х и y (рис. 2.5.в ) и построим рисунок квадрата ABCD. В квадрате определим промежуточные точки 5, 6, 7, 8, так же, как на рисунке 2.5.а

(в)
Рисунок 2.5 – Построение окружностей

(г)
Рисунок 2.5 – Построение окружностей
Соединив точки 1,5,2,6,3,7,4, 8, 1, получим изометрию окружности - эллипс (рис. 2.5.г).
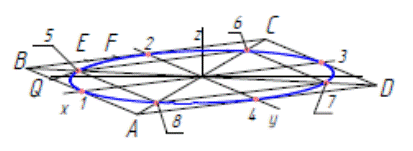
(д)
Рисунок 2.5 – Построение окружностей
Так же строится эллипс в прямоугольной диметрии (рис. 2.5.д). Последовательность построения та же, что и в изометрии, только длина по оси y уменьшится в два раза.
На рисунках 2.5.е и 2.5.ж показаны построения изометрической проекции окружности, расположенной параллельно фронтальной (рис. 2.5.е) и профильной (рис. 2.5.ж) плоскостям проекций.
В прямоугольной диметрии при изображении окружности получаются два вида рисунков эллипсов: широкий (рис. 2.5.з) и узкий (рис. 2.5.и). Принцип построения рисунков широкого и узкого эллипсов не отличается от только что рассмотренного построения рисунка эллипса в изометрии. Разница только в том, что у узкого эллипса горизонтальные стороны квадрата будут иметь угол наклона не 30º, а 7º и по линиям, параллельным оси y, размеры уменьшаются в два раза.
|
|
|

е ж
Рисунок 2.5 – Построение окружностей
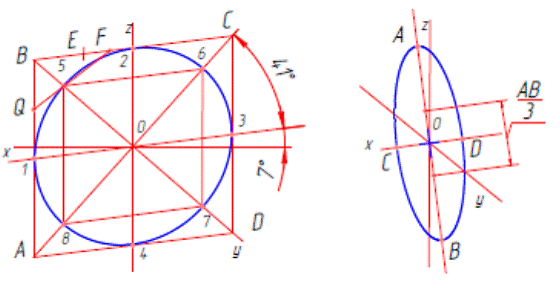
з и
Рисунок 2.5 – Построение окружностей
При выполнении рисунка узкого эллипса можно обойтись без дополнительных построений. Рисунок эллипса в таком случае выполняется по четырем точкам A,B,C,D. Как известно, в прямоугольной диметрии большая ось эллипса АВ = 1,06 D(диаметра), а малая ось CD = 0,35 D (диаметра), т. е. упрощенно, соотношение осей будет равно 1: 3. Проведем две перпендикулярные прямые (рис. 2.5.к ). От точки пересечения (т. О) этих прямых отложим на горизонтальной прямой влево и вправо половину большой оси АВ. Ось АВ возьмем равной диаметру окружности. Разделим, ось АВ на три равные части. Малая ось CD должна быть равна одной трети АВ.

(к)
Рисунок 2.5 – Построение окружностей
Построение рисунка эллипса начнем с рисования больших дуг, проходящих через точки С и D. Далее нарисуем две малые дуги, проходящие через точки А и В, а затем наметим общую огибающую кривую эллипса, так чтобы он был
симметричен относительно осей АВ и CD.

(л)
Рисунок 2.5 – Построение окружностей
Окружность в изометрии также можно построить и другим способом: по 4 точкам. Проведем две перпендикулярные прямые (рис. 2.5.л ). Отложим от точки О на горизонтальной линии два равных радиусу окружности отрезка и обозначим точками А и В. Затем отрезок АВ разделим на 5 равных частей. На вертикальной линии между точками C и D должно разместиться три таких же отрезка. Точки C и D расположены симметрично относительно оси АВ.
Построение пятиугольника
Рисунок пятиугольника начинается с построения квадрата, в который вписывается окружность (см. построение окружности рис. 2.5.а, рис. 2.5.б). После того как построена окружность, вписанная в квадрат: верхнюю часть оси y делим на три равные части, а нижнюю на пять равных частей. Через полученные точки 1/3 и 4/5 проведем вспомогательные горизонтальные прямые линии до пересечения их с окружностью, таким образом получим точки В, А, Е, D, а точка С совпадает с окружностью (рис. 2.6.а). Соединив их, получим пятиугольник.
На рисунках построен правильный пятиугольник в изометрической (рис. 2.6.б) и диметрической (рис. 2.6.в) проекциях. Строятся они в той же последовательности, что и на рисунке 2.6.а, с той лишь разницей, что в диметрии, по оси y следует откладывать половину действительного размера сторон квадрата, в
котором расположен пятиугольник.
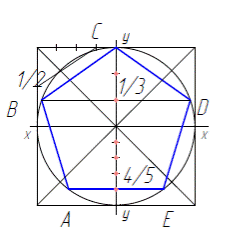
| 
|
| а | б Изометрическая проекция |
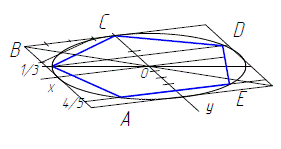
в
Диметрическая проекция
Рисунок 2.6 – Построение пятиугольника
Упражнения в рисовании плоских фигур являются хорошей подготовкой к рисованию геометрических тел, так как построение рисунков геометрических
тел основывается на умении выполнять рисунки плоских фигур.
|
|
|


