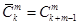Правила решения комбинаторных задач

В основе науки «Комбинаторики» лежит теория множеств. Множество – это основное понятие теории множеств, поэтому никак не определяется, а поясняется на примерах (множество натуральных чисел, множество треугольников, квадратов).

В математике изучают не только те или иные множества, но и отношения, взаимосвязи между ними. Например, известно, что все натуральные числа являются целыми, т. е. множество натуральных чисел является подмножеством множества целых чисел. Множество В называют подмножеством множества А, если каждый элемент множества В является также элементом множества А.

Используя 2 цифры, например, 3 и 5, можно записать 4 двузначных числа: 35, 53, 33 и 55. Несмотря на то, что числа 35 и 53 записаны с помощью одних и тех же цифр, эти числа различные. В том случае, когда важен порядок следования элементов, говорят об упорядоченных наборах элементов. Такие наборы называют кортежами и различают по длине. Длина кортежа – это число элементов, из которых он состоит. Например, (3; 6; 7) – это кортеж длины 3. 

Рассматривают в математике и декартово произведение множеств. Декартовым произведением множеств А₁, А₂, …, А _n называют множество всех кортежей длины n, первая компонента которого принадлежит множеству А, вторая – множеству А₂, …, n -я множеству А _n.

Если в множестве А содержится а элементов, а в множестве В – b элементов, то в декартовом произведении множества А и В содержится а· b элементов, т. е. n (A × B)= n (A)· n (B)= a · b [23, 6].

Задача: сколько двузначных чисел можно записать, используя цифры 5, 4 и 7?

Решение: запись любого двузначного числа состоит из двух цифр и представляет собой упорядоченную пару. В данном случае эти пары образуются из элементов множества А ={5, 4, 7}. В задаче требуется узнать число таких пар, т. е. число элементов в декартовом произведении А×А. Согласно правилу n (A ×А)= n (A)· n (А) =3·3=9. Значит, двузначных чисел, записанных с помощью цифр 5, 4 и 7, будет 9.

Таким образом, на основе некоторых понятий теории множеств строятся основные понятия комбинаторики.

Комбинаторные задачи в начальном курсе математики решаются, как правило, методом перебора. Для облегчения этого процесса нередко используются таблицы и графы. В связи с этим необходимы определенные умения и навыки решения комбинаторных задач. Прежде всего, решая несложные комбинаторные задачи, нужно грамотно осуществлять перебор возможных вариантов.

Задача: сколько двузначных чисел можно составить, используя    цифры 1, 4 и 7?

Решение: для того чтобы не пропустить и не повторить ни одно из чисел, будем выписывать их в порядке возрастания. Сначала запишем числа, начинающиеся с цифры 1, затем с цифры 4 и, наконец, с цифры 7: 11, 14, 17, 41, 44, 47, 71, 74, 77. Таким образом, из трех данных цифр можно составить всего 9 различных двузначных чисел.

Существует единый подход к решению самых разных комбинаторных задач с помощью составления специальных схем. Внешне такая схема напоминает дерево, отсюда название – дерево возможных вариантов. При правильном построении дерева ни один из возможных вариантов решения не будет потерян. Знак * изображает корень дерева, ветви дерева – различные варианты решения [15, 115].

Правило суммы

В комбинаторике, которая возникла раньше теории множеств, правило нахождения числа элементов объединения двух непересекающихся конечных множеств называют правилом суммы и формулируют в таком виде.

Если объект а можно выбрать m способами, а объект b – k способами (не такими, как а), то выбор «либо а, либо b» можно осуществить m + k способами.

п(А+В)=п(А)+п(В)

 

Задача: на тарелке лежат 5 яблок и 4 апельсина. Сколькими способами можно выбрать один плод?

Решение: по условию задачи яблоко можно выбрать пятью способами, апельсин – четырьмя. Так как в задаче речь идет о выборе «либо яблоко, либо апельсин», то его, согласно правилу суммы, можно осуществить 5+4=9 способами.

Правило произведения

Правило нахождения числа элементов декартова произведения двух множеств называют в комбинаторике правилом произведения и формулируют в таком виде.

Если объект а можно выбрать m способами, а объект b - k способами, то пару (a, b) можно выбрать m ∙ k способами.

п(А × В)=п(А) × п(В)

 

Правило суммы и произведения, сформулированные для двух объектов, можно обобщить и на случай t объектов.

Задача: сколько трехзначных чисел можно составить, используя цифры 7, 4 и 5?

Решение: в данной задаче рассматриваются трехзначные числа, так как цифры в записи этих чисел могут повторяться, то цифру сотен, цифру десятков и цифру единиц можно выбрать тремя способами каждую. Поскольку запись трехзначного числа представляет собой упорядоченный набор из трех элементов, то, согласно правилу произведения, его выбор можно осуществить 27 способами, так как 3∙3∙3=27.

Правила суммы и произведения – это общие правила решения комбинаторных задач. Кроме них в комбинаторике пользуются формулами для подсчета числа отдельных видов комбинаций, которые встречаются наиболее часто. Рассмотрим некоторые из них и, прежде всего те, знание которых необходимо [24, 72].

Размещения

С теоретико-множественной точки зрения запись любого двузначного числа – это кортеж длины двух. Записывая различные двузначные числа с помощью цифр 7, 4 и 5, мы по сути дела образовывали из данных трех цифр различные кортежи длины двух с повторяющимися элементами. В комбинаторике такие кортежи называют размещениями с повторениями из трех элементов по два элемента.

Размещение с повторениями из k элементов по m элементов – это кортеж длины m, составленный из m элементов k -элементного множества.

= k^m

Из определения следует, что два размещения из k элементов по m элементов отличаются друг от друга либо составом элементов, либо порядком их расположения.

Например, два двузначных числа из перечисленных выше (а это размещения из трех элементов по два) отличаются друг от друга либо составом элементов (74 и 75), либо порядком их расположения (74 и 47).

Задача: сколько всевозможных двузначных чисел можно записать, используя цифры 7, 4 и 5?

Решение: пользуясь формулой = k^m, легко подсчитать, сколько двузначных чисел можно записать, используя цифры 7, 4 и 5. так как речь идет о размещениях с повторениями их трех элементов по два, то = 3²=9.

Нередко встречаются задачи, в которых требуется подсчитать число кортежей длины m, образованных из k элементов некоторого множества, но при условии, что элементы в кортеже не повторяются. Такие кортежи называются размещениями без повторений из k элементов по m элементов.

Размещение без повторений из k элементов по m элементов – это кортеж длины m, составленный из неповторяющихся элементов множества, в котором k элементов.

 

,

              m множителей

 

Задача: сколько всевозможных трехзначных чисел можно записать, используя цифры 7, 4 и 5, так, чтобы цифры в записи числа не повторялись?

Решение: в задаче рассматриваются размещения без повторений из трех элементов по три, и их число можно подсчитать по формуле: 

=3(3-1)∙(3-2)=3∙2∙1=6.

Эти числа таковы: 745, 754, 475, 457, 547, 574.

Одним из видов размещений являются перестановки.

Перестановки

Два размещения без повторений из n элементов по m состоят из одних и тех же элементов, расположенных в различном порядке. Такие размещения называют перестановками без повторений из n элементов.

 

          где n! =1∙2∙3 ∙…∙ n

 

Читают «n факториал». Считают, что 1!=1, 0!=1. Например, 5!=1∙2∙3∙4∙5=120; 7!=1∙2∙3∙4∙5∙6∙7=5040.

Задача: сколькими способами можно расставить на шахматной доске 8 одинаковых ладей, так, чтобы никакие две из них не били друг друга?

Решение: ладьи не будут бить друг друга тогда и только тогда, когда на каждой горизонтали и каждой вертикали стоит ровно одна ладья. Поэтому будем выставлять их по горизонталям. Первую можно поставить на любые 8 полей первой горизонтали, вторую на 7 полей второй горизонтали (одна вертикаль уже занята первой ладьей) и т.д. Получаем Р₈=8!=40320 способов.

Пусть дан кортеж длинны п, составленный из элементов множества Х= { х₁, …, х _k }. Причем элемент х₁ входит в этот кортеж п₁ раз, элемент х _k – п _k раз. Тогда п=п₁+…+п _k. Если переставлять в этом кортеже буквы, то будут получаться новые кортежи, имеющие тот же состав. Эти кортежи называются перестановками с повторениями из элементов х₁,…, х _k, имеющими состав (п₁, …, п _k).

 

 

Задача: сколько различных кортежей получится, если переставлять буквы слова «математика»?

Решение: это слово имеет состав: м – 2, а – 3, т – 2, е – 1, и – 1, к – 1, то есть (2, 3, 2, 1, 1, 1), поэтому получим Р(2,3,2,1,1,1)=

В размещениях и перестановках важен порядок размещения элементов кортежа.

Сочетания

В отличие от размещений, в сочетаниях порядок элементов множества не важен.

Из элементов множества Х ={7, 4, 5} можно образовывать не только кортежи различной длины, но и различные подмножества, например двухэлементные. В комбинаторике их называют сочетаниями без повторений из трех элементов по два элемента.

Сочетание без повторения из k элементов по m элементов – это m -элементное подмножество множества, содержащего k элементов.

 

 

Два сочетания из k элементов по m элементов отличаются друг от друга хотя бы одним элементом.

Число всевозможных сочетаний без повторений из k  элементов по m элементов обозначают  [23, 154].

Задача: четыре человека сыграли друг с другом по одной партии в шахматы. Сколько было сыграно партий?

Решение: каждую партию можно рассматривать как комбинацию из двух элементов четырех элементного множества, в которой порядок расположения элементов не существен. Но такие комбинации являются сочетаниями без повторений из 4 элементов по 2 и их число равно:

Сочетанием с повторениями из n элементов по k элементов называется всякая последовательность из k элементов, членами которой являются элементы n [29].

 

=

 

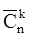Задача: сколько наборов из 7 пирожных можно составить, если в продаже имеется 4 сорта пирожных?

Решение:  = = =  = =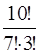120.

В комбинаторике решаются задачи, связанные с рассмотрением множеств и составлением различных комбинаций из элементов этих множеств. В зависимости от правил составления можно выделить три типа комбинаций: перестановки, размещения, сочетания [28].

Конечно, применение формул облегчает подсчет числа возможных вариантов решений той или иной комбинаторной задачи. Однако чтобы воспользоваться формулой, необходимо определить вид комбинаций, о которых идет речь в задаче, что бывает сделать не очень просто.

 

Виды комбинаций