 |
Методика обучения решению комбинаторных задач
|
|
|
|
В комбинаторных задачах заложены большие возможности для развития мышления учащихся. Кроме того, в процессе обучения решению комбинаторных задач можно расширить знания учащихся о самой задаче, познакомить их с новым способом решения задач; подготовить к решению жизненных практических проблем, научить принимать оптимальное в данной ситуации решение; организовать элементарную исследовательскую и творческую деятельность учащихся.
В процессе решения комбинаторных задач учащиеся приобретают опыт хаотичного перебора возможных вариантов. И на основе этого опыта в дальнейшем можно будет обучать детей организации систематического перебора.
Выделяют три этапа обучения комбинаторным задачам в 5 классе:
1. Подготовительный.
2. Решение задач с небольшим числом возможных вариантов.
3. Работа с графическими средствами.
На подготовительном этапе идет работа над совершенствованием мыслительных операций (анализа, синтеза, сравнения), которые входят в состав деятельности при решении комбинаторных задач. Особое внимание уделяется сравнению объектов, состоящих из отдельных элементов. В этом случае сравнение может быть проведено по таким основаниям, как: числу элементов; составу, входящих в объект элементов; порядку расположения элементов в объекте. Например, предлагаются следующие задания:
1. Рассмотри внимательно колечки из бусинок. Скажи, что изменяется от одного колечка к другому.
 |
Рис. 1
2. Вставить пропущенные числа:
1) 24, 21, 19, 18, 15, 13, _, _, 7,6 (12, 9);
2) 1, 4, 9, 16, _, _, 49, 64, 81, 100 (25, 36);
3) 16, 17, 15, 18, 14, 19, _, _ (13, 20);
4) 2 5 9 (2+4):2=3
4 7 5 (5+7):2=6
3 6? (9+5):2=7
5) 12 (56) 16 (12+16)∙2=56
|
|
|
17 (__) 21 (21+17) ∙2=76
3. Решить задачу:
Мальчик написал число 86, затем увеличил его на 12, не производя записи. Как он это сделал? (перевернул его)
На втором этапе школьники учатся находить все возможные варианты в комбинаторных задачах, организуя перебор в определенной системе. Но здесь решаются задачи с небольшим числом возможных вариантов. Основная цель этого этапа – обучение школьников решению комбинаторных задач с использованием систематического перебора всех возможных вариантов [2, 43].
Каким же образом можно подвести учеников к идее организации перебора в определенной системе, как мотивировать переход от хаотичного к систематическому перебору?
Разыгрывается следующая ситуация: Маша, Саша и Даша едут в электричке на дачу. Они сидят на одной скамейке (трое детей садятся у доски на стулья в любом порядке). Детям нужно было проехать 8 остановок. Чтобы не было скучно ехать, они решили на каждой остановке меняться местами. Ставится вопрос «Смогут ли дети каждый раз меняться местами так, чтобы их новое расположение оказывалось все время отличным от предыдущих?». Ученики предлагают варианты расположения детей, они проигрываются у доски и записываются. Пока перебор осуществляется случайным образом, хаотично. После того как найдены 6 расположений, ученики стараются еще составить другой, новый вариант. Все их попытки сделать это не приводят к успеху. Встает вопрос «Почему они не нашли седьмой вариант: не могут это сделать или его не существует и уже найдены все возможные расположения?». Чтобы ответить на него, учащимся предлагается рассмотреть составленные 6 вариантов, найти и записать пары вариантов, очень похожие друг на друга. Например, можно выделить такие тройки:
М. С. Д. С. Д. М. Д. М. С.
М. Д. С. С. М. Д. Д. С. М.
Полученная последовательность вариантов анализируется. Учащиеся замечают, что все девочки сидели у окна и, когда одна из них сидит у окна, то две другие могут разместиться только двумя различными способами. Таким образам, дети убеждаются в том, что можно составить только 6 различных вариантов, других быть не может. Затем учитель просит учеников по записанным вариантам еще раз рассказать, какой способ пересаживания был выбран во втором случае. И обращает внимание на то, что, используя его, можно быстро составить варианты, не повторяя дважды одни и те же, и быть уверенным, что найдены все возможные варианты. В дальнейшем решение задач хаотичным перебором не запрещается. Но те ученики, которые проводят перебор по определенной системе, поощряются. Предложенные ими способы разбираются и подчеркиваются преимущества осуществления такого перебора. Постепенно дети убеждаются в пользе систематического перебора и приучаются его использовать.
|
|
|
В одной и той же задаче можно выбрать разную систему перебора, и каждый ученик сам решает, как он будет действовать. Так, например, при решении приведенной выше задачи можно было ориентироваться на сидящего посередине (или у прохода):
С.М.Д. М.С.Д. М.Д.С. С.М.Д. М.Д.С. Д.С.М
Д.М.С. Д.С.М. С.Д.М. М.С.Д. Д.М.С. С.Д.М.
Можно предложить учащимся использовать прием, заключающийся во временном уменьшении числа элементов и составлении требуемых в задаче комбинаторных соединений на основе найденных вариантов для меньшего числа элементов. Например, задача: «Сколько разных фигур можно составить на листе бумаги из четырех одинаковых квадратов при условии, что квадраты соприкасаются точно по сторонам?» Чтобы ее решить, учитель предлагает детям сначала все возможные фигуры из трех квадратов. Затем взять первую фигуру, составленную из трех квадратов, и по-разному присоединять к ней четвертый квадрат, следя за тем, чтобы не получились одинаковые фигуры. Также предлагается действовать и со второй фигурой, составленной из трех квадратов (рис 2).
Рис. 2
Рис. 3
После того как школьники убедятся в преимуществе систематического перебора, им следует показать, что есть и такие задачи, в которых не стоит искать какую-либо систему перебора. Это задачи комбинаторной геометрии. Комбинаторная геометрия – это раздел математики, который занимается вопросами расположения и комбинаций фигур. Например, нужно из деталей, изображенных на рис. 3, выложить «лесенку», по заданному контуру (рис. 4). Различные решения (рис. 5, 6, 7,) находятся в процессе хаотичного перебора, так в этой задаче можно быстрее и легче выполнить требуемое.
|
|
|
Рис. 4 Рис. 5 Рис. 6 Рис. 7
При решении комбинаторных задач в некоторых случаях у школьников могут возникать затруднения в различении составляемых соединений, связанных с тем, что для определения их неразличимости нужно выполнить определенные геометрические преобразования.
Составление комбинаторных соединений происходит с опорой на запись. Следовательно, в задачах, в которых элементы являются реальными предметами, стоит проблема их обозначения. И если в начале обучения используются конкретные, наглядные заместители реальных предметов, то в дальнейшем учащиеся постепенно переходят к применению условных обозначений. Например, задача: «На каждом флажке должны быть три горизонтальные полоски: красного, синего и белого цвета. Сколько можно получить различных флажков, если менять порядок расположения цветов?» Решая ее, можно выбрать различные способы обозначения флажков.
|
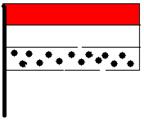Рис. 8
Непосредственный перебор всех возможных вариантов при решении комбинаторных задач в некоторых случаях может быть затруднен. Облегчить процесс нахождения этих вариантов можно, научив детей пользоваться такими средствами перебора, как таблицы и графы. Они позволяют расчленить ход рассуждений, четко провести перебор, не упустив каких-либо имеющихся возможностей. Решение задач с использованием таблиц и графов является основным содержанием третьего этапа, выделяемого в обучении школьников решению комбинаторных задач.
|
|
|
Сначала как с наиболее простым средством организации перебора учащиеся знакомятся с таблицами. Рассматривая таблицу (рис. 9) ученики открывают принцип её составления. Затем им предлагают заполнить другую таблицу. Проговариваются разные способы заполнения: по строчкам, по столбцам.
В дальнейшем в целях освоения принципа составления таблиц используются и такие задания:
1. Запиши в нужные клетки таблицы (рис. 10) следующие числа: 57, 75, 44, 47, 55, 77, 47. Какие числа нужно записать в оставшиеся клетки?
2. Проверь, правильно ли заполнена таблица (рис. 11).
Когда школьники научатся составлять таблицы, можно переходить к решению комбинаторных задач с их использованием. Как правило, дети неоправданно много времени тратят на вычерчивание самой таблицы: затрудняются определить нужные размеры, разметить все строчки и столбики.
Для того чтобы помочь детям разметить таблицу, методистами были разработаны специальные трафареты (рис. 12). Опишем, как действуют учащиеся, решая с помощью таблицы задачу: «В одной деревне по сложившейся традиции мужчин называют каким-либо из следующих имен: Иван, Петр, Василий и Михаил. Проживают в этой деревне 15 мужчин. Может ли оказаться так, что в деревне нет мужчин с одинаковым именем, отчеством?» Ученик накладывает на тетрадный лист трафарет. Вписывает через «окошечки» на трафарете в верхнюю строчку и в первый столбик данные задачи. Через прорези намечает места записи составляемых объектов. Убирает трафарет. Цветными линиями отчерчивает данные задачи (рис. 13).
Затем ученик заполняет таблицу (рис. 14), подсчитывает число всех возможных отличающихся имен-отчеств, сравнивает с числом мужчин в деревне и отвечает на вопрос задачи.
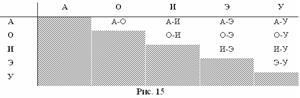При заполнении таблиц нужно каждый раз определять, следует записывать составляемое
Рис. 16
Составляются недостающие рукопожатия (эти линии лучше проводить другим цветом, так как потом легче будет подсчитывать общее число рукопожатий). И так действуют до тех пор, пока все не поздороваются друг с другом. По получившемуся графу (рис. 16) подсчитывается число рукопожатий (их всего 10).
Следующая задача: «Сколько двузначных чисел можно составить, используя цифры 1, 2, 3, 4?» приводит учащихся к изображению ориентированного графа (рис. 17). Идея проведения стрелок возникает, когда учащиеся задумываются
Рис. 17
как обозначить, например, число 12: показать, что оно начинается с цифры 1, а оканчивается цифрой 2. петля появляется при обозначении, например, числа 11: стрелка должна начинаться и заканчиваться на одной и той же цифре. Открыв для себя на первых задачах эти условные обозначения (точки, линии, стрелки, петли), учащиеся в дальнейшем применяют их при решении различных задач, составляя графы того или иного вида. Приведем некоторые примеры.
|
|
|
1. В финал турнира по шашкам вышли два российских игрока,
Рис. 18
два немецких и два американских. Сколько партий будет в финале, если каждый играет с каждым по одному разу и представители одной страны между собой не играют? (граф на рис. 18)
Рис. 19
2. В зале лежали конфеты четырех сортов. Каждый ребенок взял по 2 конфеты. И у всех оказались отличающиеся наборы конфет. Сколько могло быть детей? (граф на рис. 19)
3. Сколько разностей можно составить из чисел 30, 25, 17, 9, если для их составления брать по 2 числа? Будут ли среди них разности, значения которых равны? (граф на рис. 20)
Можно предлагать учащимся и обратные задания: составить задачу по имеющемуся графу. Например: «Рассмотри внимательно граф (на рис. 21) и пофантазируй, о какой ситуации он может тебе рассказать». Ученики, рассуждая, что точки могут обозначать людей, предметы, а линии говорят о том, что из них образуются пары, составляют разные варианты задач, например
Рис. 20 Рис. 21
1. Четыре подружки вечером по телефону созваниваются друг с другом. Сколько звонков было сделано, если каждая подружка поговорила с каждой по одному разу?
2. В магазине продаются елочные шары четырех видов. Сколько отличающихся наборов, состоящих из двух разных шаров, можно с, состоящих из двух разных шаров, можно составить?
Примеры задач, которые можно решать с помощью таблиц и графов:
1. На фабрике есть стержни для ручек четырех цветов: красного, синего, зеленого и черного. Сколько различных трехцветных ручек можно при этом собрать?
2. У девочки есть бумага зеленого и желтого цвета. Из нее она вырезает круги, квадраты и треугольники, делая их большими и маленькими. Сколько различных вариантов у нее получится?
3. Шерлоку Холмсу нужно открыть сейф, для этого он должен отгадать код. Он знает, что код – это трехзначное число, составленное из цифр 1, 2, 3, 4 и большее числа 400. Какие числа должен проверить Шерлок Холмс, чтобы найти код?
Правила решения комбинаторных задач и представленная методика обучения решению комбинаторных задач может помочь учителю в разработке уроков.
Таким образом, если это будут не разрозненные сведения из комбинаторики, а факультативный курс, то повысится эффективность обучения, так как задачи такого вида часто включаются в олимпиадные задания. Поэтому автором данной работы была разработана программа факультативного курса по теме «Элементы комбинаторики» для 8 класса.
|
|
|
