Применение закона Био-Савара-Лапласа для нахождения магнитного поля

 

1. Магнитное поле прямого тока — тока, текущего по тонкому прямому проводу бесконечной длины (рис. 11).

Рисунок 11

 

В произвольной точке А, удаленной от оси проводника на расстояние R, векторы d B от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа («к вам»). Поэтому сложение векторов d B можно заменить сложением их модулей. В качестве постоянной интегрирования выберем угол a (угол между векторами d l и r), выразив через него все остальные величины. Из рис. 11 следует, что

 

(радиус дуги CD вследствие малости d l равен r, и угол FDC по этой же причине можно считать прямым). Подставив эти выражения в (7), получим, что магнитная индук­ция, создаваемая одним элементом проводника, равна

(9)

 

Так как угол a для всех элементов прямого тока изменяется в пределах от 0 до p, то, согласно (8) и (9),

(10)

 

Следовательно, магнитная индукция поля прямого тока

(11)

 

 

38. 2. Магнитное поле в центре кругового проводника с током (рис. 12).

 

 

Рисунок 12

 

Как следует из рисунка, все элементы кругового проводника с током создают в центре магнитные поля одинакового направления — вдоль нормали от витка. Поэтому сложение век­торов d B можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (sin a =1) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то, согласно (7),

(12)

 

 

Тогда

(13)

 

Следовательно, магнитная индукция поля в центре кругового проводника с током

(14)

 

 

3. Магнитное поле витка с током в произвольной точке на оси витка.

На рис.13 показан круговой виток радиуса R, плоскость которого перпендикулярна плоскости чертежа, а ось ОО^/ лежит в этой плоскости.

Рисунок 13

 

В точке С на оси ОО^/ векторы для полей различных малых элементов витка с током I не совпадают по направлению. Векторы и для полей двух диаметрально противоположных элементов витка и , имеющих одинаковую длину (), равны по модулю:

Результирующий вектор направлен в точке С по оси ОО^/ витка, причем

Вектор индукции в точке С для магнитного поля всего витка направлен также вдоль оси ОО^/, а его модуль

(15)

Если воспользоваться понятием вектора магнитного момента витка с током I, то выражение (15) можно переписать в форме

(16)

(17)

 

39. а)Теорема о циркуляции : циркуляция вектора по произвольному замкнутому контуру равна произведению магнитной постоянной 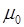на алгебраическую сумму токов, охватываемых этим контуром:

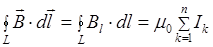, (37)

где 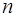- число проводников с токами, охватываемых контуром произвольной формы.

 

б) Если

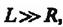
то соленоид можно приближенно считать бесконечно длинным. Для точки А, лежащей вдали от концов такого соленоида , а , так что по формуле (18),

(19)

В точке А, находящейся в центре одного из оснований бесконечно длинного соленоида (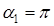, и ),

(20)

Магнитный момент соленоида равен геометрической сумме магнитных моментов всех его витков :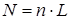

, (21)

где , а - единичный вектор, направленный по оси соленоида в ту же сторону, что и вектор . Модуль магнитного момента соленоида

(22)

где - объем соленоида.

 

 

40. 4. Магнитное поле соленоида.

Соленоидом называется цилиндрическая катушка с током, состоящая из большого числа витков проволоки, которые образуют винтовую линию. Если витки расположены вплотную или близко друг к другу, то соленоид можно рассматривать как систему последовательно соединенных круговых токов одинакового радиуса с общей осью. На рис.14 показано сечение соленоида радиуса R и длины L с током I. Кружки с точками изображают сечения витков, в которых электрический ток направлен из-за чертежа к нам, а кружки с косыми крестиками – сечения витков, в которых ток направлен за чертеж. Пусть n – число витков, приходящихся на единицу длины соленоида.

Рисунок 14

 

Магнитная индукция поля соленоида равна геометрической сумме магнитных индукций полей всех витков этого соленоида. В произвольной точке А, лежащей на оси соленоида О₁О₂, все векторы и результирующий вектор направлены по оси О₁О₂ в ту сторону, куда перемещается буравчик с правой резьбой при вращении его рукоятки в направлении электрического тока в витках соленоида. На малый участок соленоида длиной вдоль оси приходится витков. Если l – расстояние вдоль оси от этих витков до точки А, то, согласно (16), магнитная индукция поля этих витков

 

Так как

то

и

В пределах соленоида угол изменяется от до , поэтому

(18)

 

 

41. * Теорема о циркуляции вектора магнитной индукции. Получите с помощью этой теоремы выражение для нахождения индукции магнитного поля бесконечно длинного проводника с током.

Явление электромаг­нитной индукции - заключается в том, что в замкнутом проводящем контуре при изменении потока магнитной индукции, охватываемого этим контуром, возникает электрический ток, получивший название индукционного.

Вектор магнитной индукции – физическая величина, характеризующая магнитное поле точно так же, как и напряженность электрического поля характеризует электрическое поле.

Циркуляцией вектора напряженности В по заданному контуру называется интеграл (берется по замкнутому контуру):

B _{l =} B cos α

Найдем циркуляцию вектора B по контуру в виде окружности, охватывающей бесконечный прямой проводник с током.

Пусть плоскость этой окружности перпендикулярна проводнику с током, центр её находится на проводнике. Выбранный нами контур совпадает с линией магнитной индукции прямого проводника (силовой линией).

Значение вектора В вдоль силовой линии равно по формуле:

B =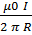

Где R – радиус окружности

Циркуляция вектора B вдоль силовой линии:

= = d l

Длина дуги окружности, как известно из определения радианной меры угла, равна:

d l= R dφ

Подставляя значение d l в выражение для циркуляции вектора B вдоль силовой линии и вынося постоянные величины, получаем:

= =μ₀I

Теорема:

Циркуляция вектора по произвольному, замкнутому контуру равна алгебраической сумме токов, охватываемых контуром, умноженной на μ₀, т.е.

= μ₀

42. Магнитное поле соленоида. Выражение для индукции магнитного поля внутри бесконечно длинного соленоида.

Соленоид – провод, навитый на цилиндрический каркас. На 1 метр длины – n витков.

N – число витков на длине l.

Магнитное поле бесконечного соленоида однородно, индукция его может быть найдена по формуле:

B=μ₀nI

где n – число витков на единицу длины соленоида, I – сила тока в соленоиде

Направлено магнитное поле вдоль оси соленоида, в соответствии с правилом правого

винта.

 

43. Действие магнитного поля на ток. Сила, действующая на элемент тока (закон Ампера) в векторной и скалярной формах.

Источник магнитного поля - электрический ток (движущийся электрический заряд). Магнитное поле действует на другой ток с силой, пропорциональной силе тока и магнитной индукции поля. На элемент тока в магнитном поле действует сила

d F =Id l

модуль вектора d F:

d F =I B d l sin α

направление определяется по правилам векторного произведения

Силу, действующую на проводник с током в магнитном поле называют силой Ампера. Для того, чтобы найти силу Ампера, действующую на проводник сложной формы или больших размеров, нужно разбить проводник на элементы тока и затем найти векторную сумму сил, действующих на элементы тока.

 

44. Сила, действующая на прямолинейный проводник с током.

Пусть имеются два бесконечных прямых параллельных проводника, по которым текут токи I₁ и I₂ . Ток I₁ создает в точке, где находится второй проводник, в соответствии с формулой

B =

Модуль силы Ампера, действующий на единицу длины проводника с током I2 в соответственно равен:

F₂₁=

Проводники с параллельными токами, текущими в одном направлении, взаимно притягиваются с силой, определяемой в расчете на единицу длины формулой выше. Проводники с противоположно направленными токами взаимно отталкиваются с силой, также определяемой.

45. Пусть b – расстояние между двумя параллельными, бесконечно длинными проводниками (рис. 2.2). Задачу следует решать так: один из проводников создаёт магнитное поле, второй находится в этом поле.

Магнитная индукция, создаваемая током на расстоянии b от него:

,

Рис. 2.2

Если и лежат в одной плоскости, то угол между и прямой, следовательно . Тогда сила, действующая на элемент тока ,

,

На каждую единицу длины проводника действует сила

,

(разумеется, со стороны первого проводника на второй действует точно такая же сила).

 

46. Рассмотрим плоский замкнутый контур очень малых размеров. Будем называть такой контур пробным контуром.Ориентацию его в пространстве характеризует направление нормали к контуру, восстанавливаемой по правилу правого буравчика: вращаем рукоятку правого буравчика по направлению тока в контуре, тогда направление его поступательного движения даст направление нормали (см. рис. 1).

Помещая пробный контур в магнитное поле, обнаружим, что поле стремится повернуть контур (нормаль) в определенном направлении.

Вращающий момент, действующий на контур, зависит как от свойств магнитного поля в данной точке, так и от свойств контура. Оказывается, что максимальная величина вращающего момента пропорциональна , т.е. ~ , где -ток контуре, - площадь контура с током, (рис. 1).

Векторную величину называют магнитным моментом контура, который в СИ измеряется в А м ².

 

 

47. На контур с током в неоднородном магнитном поле действует сила Ампера.

Результирующая сила Ампера, которая действует на контур с током в магнитном поле, определяется как:

Во внешнем магнитном поле элементарный контур с током ведет себя аналогично тому, как и электрический диполь во внешнем неоднородном электрическом поле: он будет поворачиваться к положению устойчивого равновесия и, кроме того, как можно показать, под действием результирующей силы Ампера втягиваться в область более сильного поля.

 

48. Если поместить в магнитное поле не проводник, а виток (или катушку) с током и расположить его вертикально, то, применяя правило левой руки к верхней и нижней сторонам витка, получим, что электромагнитные силы F, действующие на них, будут направлены в разные стороны. В результате действия этих двух сил возникает электромагнитный вращающий момент М, который вызовет поворот витка, в данном случае по часовой стрелке. Этот момент

M = FD

где D — расстояние между сторонами витка.
Виток будет поворачиваться в магнитном поле до тех пор, пока он не займет положение, перпендикулярное магнитным силовым линиям поля. При таком положении через виток будет проходить наибольший магнитный поток. Следовательно, виток или катушка с током, внесенные во внешнее магнитное поле, всегда стремятся занять такое положение, чтобы через виток проходил возможно больший магнитный поток. Свойство витка и катушки с током поворачиваться в магнитном поле широко используется в электротехнике; электрические двигатели и ряд электроизмерительных приборов работают по этому принципу.

Для увеличения вращающего момента в электрических двигателях применяют не один виток, а несколько. Эти витки, соединенные соответствующим образом, образуют обмотку якоря электродвигателя.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: