Описание лабораторной установки

Министерство образования и науки

Российской Федерации

Федеральное государственное

бюджетное образовательное учреждение

высшего профессионального образования

Национальный исследовательский ядерный университет

«МИФИ»

Волгодонский инженерно-технический институт –филиал

НИЯУ МИФИ

 

 

Е.С.Молошная, О.В.Фоменко, И.Н. Садавова

Электрические цепи однофазного

Синусоидального тока

Методические указания к лабораторным работам

по дисциплине «Электротехника и электроника»

 

 

Волгодонск 2012

 

УДК 621.3.025 (076.5)

М 75

Рецензенты: канд. техн. наук, доц. А.А. Баранник

 

электрические цепи однофазного синусоидального тока: метод.указания к лабораторным работам по электротехнике и основам электроники

/Е. С. Молошная, О.В. Фоменко, И.Н. Садавова; ВИТИ НИЯУ МИФИ. - Волгодонск, 2012.-20с.

Настоящие методические указания имеют цель оказать помощь студентам при самостоятельной подготовке и выполнении лабораторных исследований по курсу «Электротехника и электроника» раздел «Электрические цепи однофазного синусоидального тока».

Цель настоящие методических указаний – оказать помощь студентам при выполнении лабораторных работ по курсу «Электротехника и электроника», раздел «Электрические цепи постоянного тока».

Указания предназначены для студентов 3, 4 по направлениям 140400 «Электроэнергетика и электротехника», 140700 «Ядерная энергетика и теплофизика», 141403 «Атомные станции: проектирование, эксплуатация и инжиниринг», 140100 «Теплоэнергетика и теплотехника», 150700 «Машиностроение» профиль "Оборудование и технология сварочного производства", 271101 «Строительство уникальных зданий и сооружений», 141100 "Энергетическое машиностроение", 210100 «Электроника и наноэлектроника», 270800 «Строительство», 280700 «Техносферная безопасность» всех форм обучения.

Рекомендованы для использования в учебном процессе на заседании кафедры «Атомные электрические станции», протокола № 10, от 18.04.2012 г.

©ВИТИ НИЯУ МИФИ, 2012

ЛАБОРАТОРНАЯ РАБОТА № 1

 

Исследование линейной цепи синусоидального тока при последовательном соединении приемников

 

Цель работы. Экспериментально исследовать влияния параметров электрической цепи переменного тока на значения электротехнических величин: тока, напряжения, мощности, cosφ; определить параметры цепи по результатам измерений в различных режимах; проанализировать режим резонанса напряжения.

 

Программа работы

1.1 Ознакомиться со схемой установки (рис.1.1) и измерительными приборами. Записать данные приборов и их типы в таблицу.

1.2 В цепи (рис.1.1):

- подключить осциллограф для снятия осциллограмм входного напряжения и тока. На вход Х-Х осциллографа подать напряжение с шунта R _ш, а на вход y-y – входное напряжение;

- включить цепь с помощью тумблера F;

- настроить цепь в резонанс путем изменения индуктивности дросселя (первоначально сердечник полностью выведен), наблюдая на экране осциллографа совмещение осциллограмм входного напряжения и тока в цепи;

- измерить действующие значения входного напряжения U, тока в цепи I, напряжение на индуктивной катушке U _k и на конденсаторе U_с, активную мощность, потребляемую в цепи P. Данные опытов внести в таблицу 1.1;

- рассчитать коэффициент мощности цепи cosφ и фазовый угол φ. Полученные расчеты занести в таблице 1.1.

Рисунок 1.1 Принципиальная схема исследуемой цепи

1.3 Расстроить резонансный режим один раз уменьшив,а другой раз увеличив индуктивность дросселя. Снять осциллограммы и повторить все измерения и расчеты п. 1.2, для этих двух режимов. Данные занести в таблицу 1.1.

1.4 Построить векторные диаграммы токов и напряжений для трех режимов φ>0; φ=0; φ<0.

1.5 Исследовать последовательную цепь R, L, C с помощью программы Multisim 10.

Таблица 1.1-Данные опытов и расчетов

 

№ пп.

U,В

f,Гц

U 1, В

U 2, В

I, А

P, Вт

cosφ

φ, град

R, Ом

XL , Ом

XC , Ом

Q, BAр

S, BA

Данные опытов

Результаты расчетов

Пояснения к работе

Закон изменения любой синусоидально изменяющейся величины может быть записан в виде

(1.1)

где - мгновенное значение тока;

- максимальное значение (амплитуда);

- фаза;

- начальная фаза (при t= 0);

- угловая частота;

- частота, Гц.

Связь между током и напряжением для мгновенных значений на элементах R, L, C вычисляется по формулам:

; (1.2)

(1.3)

(1.4)

 

 

а) б)

 

Рисунок 1.2 - Временная диаграмма синусоидального тока (а) и его векторная диаграмма (б)

 

На схемах стрелками показывают условно положительное направление синусоидально изменяющихся величин. Стрелка означает, что именно так направлена синусоидальная величина, когда положительна в соответствии с запасом ее изменения.

Действующим называется такой не изменяющийся во времени ток, при котором в сопротивлении за время в один период выделяется то же количество теплоты, что и при постоянном токе:

(1.5)

На действующее значение градуируются шкалы электромеханических измерительных приборов.

Используя метод математического моделирования, можно синусоидально изменяющейся величине поставить в соответствие вращающийся вектор, позволяющий определить фазу и мгновенное значение в любой момент времени. Это позволяет перейти от дифференциальных уравнений, написанным для мгновенных значений токов и напряжений, к алгебраическим уравнениям и значительно упрощает расчет цепей переменного тока.

Для анализа и расчета широко используются векторные диаграммы – совокупность векторов, отображающих фазовые и количественные соотношения между электрическими величинами в данной цепи, вытекающие из законов Кирхгофа. При анализе и расчете электрических цепей переменного тока необходимо учитывать не только сопротивление различных их элементов, но также индуктивности и емкости, если, конечно, они имеют существенное значение. Объясняется это тем, что при переменном токе в устройствах, обладающих индуктивностью, возникает ЭДС самоиндукции, а в устройствах, обладающих емкостью, появляется изменяющееся напряжение ЭДС самоиндукции и напряжение на емкости оказывают влияние на ток, напряжение и мощность в электрической цепи.

Рассмотрим идеализированные элементы электрических цепей переменного тока, имеющие только активное сопротивление R, индуктивность L или емкость С.

Если ток в этих элементах будет изменяться по закону , то напряжения будут описываться выражениями:

(1.6)

(1.7)

(1.8)

где

где индуктивное сопротивление:

, Ом;

емкостное сопротивление:

Разделив левые и правые части соотношений между амплитудными значениями напряжений и токов на , получим соотношение между действующими значениями:

; ; (1.9)

Указанные выше соотношения, а также временные и векторные диаграммы имеют важнейшее значение для изучения синусоидального тока.

Мощность – это скорость изменения энергии. Можно говорить о мгновенной, активной, реактивной и полной мощности.

Мгновенная мощность равна произведению мгновенных значений тока и напряжения:

(1.10)

Мгновенная мощность изменяется с течением времени и по величине, и по знаку.

При активной нагрузке () в течение всего периода изменения тока р>0, в этом случае электрическая энергия потребляется из сети и обратно в сеть не возвращается. Она преобразуется в тепло, механическую энергию и т.п.

При индуктивной нагрузке (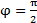), а также при емкостной нагрузке () в одну четверть периода, когда р>0, электрическая энергия забирается из сети и преобразуется в энергию магнитного или электрического поля; в другую четверть периода, когда р<0, такое же количество энергии преобразуется в электрическую энергию и возвращается в сеть.

В электрических цепях могут быть разные по величине и по характеру сопротивления (R, X_L, X_C). В соответствие с этим угол сдвига фаз между напряжением и током может лежать в пределах .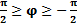

В случае смешанной активно-индуктивной () или активно-емкостной нагрузки (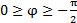) забираемая из сети электрическая энергия больше энергии, возвращаемой в сеть, так как возвращается только та часть энергии, которая была преобразована в энергию магнитного или электрического поля.

Под активной мощностью понимается мощность, равная среднему значению мгновенной мощности за период

, (1.11)

где cosφ - коэффициент мощности показывает, какую часть полной мощности, потребляемой приемником, составляет активная мощность.

Реактивная мощность, индуктивная или емкостная

. (1.12)

Реактивная мощность соответствует энергии, которая в одну часть периода забирается из сети и преобразуется в энергию магнитного или электрического поля, а в другую - вновь преобразуется в электрическую энергию и возвращается в сеть.

Полная мощность включает в себя активную и реактивную мощность:

. (1.13)

В последовательной цепи R,L,C согласно второму закону Кирхгофа в комплексной форме

(1.14)

Действующее значение входного напряжения

 

(1.15)

 

Коэффициент мощности

(1.16)

(1.17)

Мощности

; (1.18)

(1.19)

(1.20)

Резонансом напряжения называется режим работы последовательной цепи R,L,C, наступающий при равенстве индуктивного и емкостного сопротивлений:

(1.21)

Как видно, резонанс может быть получен путем изменения индуктивности, емкости или частоты. Режим резонанса напряжения характеризуется следующим образом

- полное сопротивление минимально и равно активному сопротивлению:

(1.22)

- ток в цепи максимален

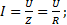(1.23)

- напряжение на индуктивности и емкости равны между собой,находятся в противофазе и могут быть по величине значительно больше входного напряжения

- ; ;

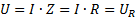- активная мощность имеет максимальное значение, ;

- реактивная мощность всей цепи равна нулю, хотя индуктивная и емкостная мощности могут иметь большие значения

Между индуктивностью и емкостью происходит обмен энергией, из сети реактивная энергия и соответствующая ей реактивная мощность не потребляются:

- полная мощность равна активной мощности: ;

- напряжение и ток совпадают по фазе: .

 

Описание лабораторной установки

В лабораторной работе производится исследование последовательной электрической цепи, включающей в себя регулируемый резистор R =0-22 Ом, конденсатор с постоянной емкостью С =10 мкФ и индуктивную катушку с регулируемым зазором (R_k =8 Ом, L_k =500-1200 мГн). Все элементы цепи смонтированы на лицевой панели стенда, там же укреплен резистор R _ш, используемый для снятия осциллограмм тока.

Для измерения тока и напряжений используются амперметр и вольтметры электромагнитной системы или мультиметр. Активная мощность измеряется ваттметром электродинамической системы.

Для исследования амплитудно-фазовых соотношений используется двухлучевой осциллограф С 1-33 (см. инструкцию по применению осциллографа).

Питание исследуемой цепи осуществляется от сети однофазного тока через понижающий трансформатор и пусковой автомат. Действующее значение питающего напряжения U =14 В.

 

Методические указания

При включении питающего напряжения сердечник катушки должен быть полностью выведен, что соответствует минимальной индуктивности. Сопротивление регулируемого реостата устанавливается преподавателем. Для осциллографирования тока на вход X-X осциллографа подается напряжение, снятое с малого сопротивления R _ш.

Масштаб тока и напряжения на осциллограммах следует определить так: по показаниям вольтметра амплитудное значение напряжения .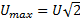

Масштаб напряжения В/мм определяется:

Масштаб тока А/мм определяется аналогично:

где I – показания амперметра, (А); l₁ –амплитуда тока на экране осциллографа (мм).

При настройке цепи в резонанс следует постепенно увеличивать индуктивность дросселя введением сердечника. При этом ток в цепи постепенно увеличивается за счет уменьшения реактивного сопротивления цепи :

где

В резонансном режиме, когда , ток максимален () и совпадает с напряжением по фазе: φ=0(см. рис. 1.3,б).

При уменьшении индуктивности уменьшается и индуктивное сопротивление катушки , в цепи будет преобладать емкостная нагрузка , ток будет опережать напряжение и действующее значение тока будет меньше, чем при резонансе

 

а) б) в)

 

Рисунок 1.3- Временные диаграммы тока и входного напряжения при различном характере нагрузки в цепи: а) φ<0 – ток опережает напряжение X_L<X_C; б) φ=0 – ток совпадает с напряжением по фазе X_L=X_C; в) φ>0 – напряжение опережает ток X_L>X_C

 

При увеличении индуктивности ток в цепи уменьшится, так как индуктивное сопротивление увеличивается и становится больше, чем емкостное. Полное реактивное сопротивление . теперь носит индуктивный характер, угол φ > 0, напряжение опережает ток по фазе (рис. 1.3,в), ток в цепи

По данным опытов рассчитываются:

- -коэффициент мощности (при резонансном режиме мощность Р максимальна и равна , );

- -

Примечание. Угол сдвига φ можно определить также из осциллограммы, измерив линейкой сдвиг фаз и период Т, тогда . Знак угла φ нужно определить по осциллограмме (рис. 1.4).

- - емкостное сопротивление конденсатора, где C указано на стенде;

- - полное сопротивление дросселя,

-

- - индуктивное сопротивление дросселя, для этого определяем активное сопротивление .

Построение векторных диаграмм удобнее начинать с вектора тока İ, так как ток через все элементы цепи течет один и тот же. Напряжение на конденсаторе отстает от тока İ на 90^о. Вектор напряжения на индуктивной катушке опережает ток İ на 90^о. Вектор входного напряжения можно построить, зная фазовый угол сдвига φ.

Примерные векторные диаграммы трех исследуемых режимов приведены на рисунке 1.4.

 

 

Рисунок 1.4 - Векторные диаграммы последовательной цепи R, L, C при постоянной частоте и емкости и переменной индуктивности а) X_C>X_L; б) X_C=X_L (резонанс напряжений); в) X_L>X_С

 

Как видно из результатов опытов и построенных векторных диаграмм, реактивные падения напряжения при резонансе будут равны друг другу по величине и противоположны по фазе. При достаточно малых величинах активного сопротивления цепи R напряжения на индуктивности и емкости в резонансном режиме могут быть во много раз выше напряжения на входе ().

123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: