 |
Указания к выполнению лабораторнойработыс помощью компьютерной программы Multisim10
|
|
|
|
]
1 Запустить программу Multisim10. Извлечь на рабочее поле из соответствующих библиотек пиктограммы элементов цепи: источник переменного напряжения V 1, установив его параметры 100 В, 50 Гц, фаза 0°; заземлитель; резистор R 1; катушку индуктивности L 1; конденсатор C 1, установив их рассчитанные или заданные параметры; источники ЭДС, управляемые током (датчики токов цепи) V 2;мультиметр XMM 1 (в режиме амперметра) для измерения тока, мультиметры XMM 2, XMM 3, XMM 4 (в режиме вольтметра) для измерения падения напряжения на элементах; вольтметр U 2 для измерения напряжения в цепи, осциллограф XSC 1.
2 Ознакомиться с измерительными приборами, и собрать электрическую цепь в Multisim по рис. 1.5, используя данные таблицы 1.3, согласно заданного варианта.
Показания мультиметра XMM 1 и датчика тока V 2 будут соответствовать общему току цепи; показания мультиметра XMM 2 будет соответствовать падению напряжения на активном сопротивлении; XMM 3 – на индуктивном, XMM 4 - емкостном сопротивлении.
Подключим вход А осциллографа к напряжению источника, а вход В попеременно подключать к выходным зажимам датчиков токов: общего тока цепи, тока резистора, катушки или конденсатора. Входные зажимы датчиков тока соединить и подключить к заземленному зажиму источника напряжения, куда необходимо подключить и заземляющий зажим осциллографа.
Оборудование:
Таблица 1.2 - Перечень необходимого оборудования
| Компонент | Изображение | Последовательность действий |
| Источник переменного напряжения | панель Виртуальных инструментов» Источники энергии (PowerSources)» Источник переменного напряжения (ACVoltageSource) | |
| Заземление | панель Виртуальных инструментов» Источники энергии (PowerSources)» Земля (Ground) | |
| Потенциометр | панель Виртуальных инструментов» Основные компоненты (BasicComponents)» Виртуальный линейный потенциометр (VirtualLinearPotentiometer) | |
| Виртуальная катушка | панель Виртуальных инструментов» Основные компоненты (BasicComponents)» Виртуальная переменная индуктивность(VirtualVariableInductor) | |
| Виртуальный конденсатор | панель Виртуальных инструментов» Основные компоненты (BasicComponents)» Виртуальный конденсатор (VirtualCapacitor) | |
| Мультиметр | Правая панель | |
| Вольтметр |

| панель Виртуальных инструментов» Измерительные приборы (MeasurementComponents)» Вольтметр (Voltmeter) |
| Ваттметр | Правая вертикальная панель |
|
|
|
| Осциллограф | Правая вертикальная панель | |
| Ключ на одно положение, управляемый клавишей | панель Компонент (Component)» Основные элементы (Basic)» список Переключатели (Switch) окна Семейство (Family)» список Компонент (Component)» Ключ (SPST) |
Таблица 1.3 – Значения параметров элементов схем
| Вариант | Значения параметров элементов ветвей | |
| R, Ом | C, мкФ | |
Рисунок 1.5 - Схема исследования цепи с последовательным соединенными резиcтором R, катушкой индуктивности L, конденсатором С
5.3.1 Эксперимент №1
При полной компенсации реактивной мощности падение напряжения на катушке индуктивности равно падению напряжения на конденсаторе, поскольку реактивные токи этих элементов не только противоположны по фазе, но и равны по величине, следовательно, равны их и реактивные мощности.
Между конденсатором и катушкой происходит непрерывный обмен реактивными мощностями. Поскольку такой обмен происходит без потерь, а по величине они равны, то цепь в целом получает от источника только активную мощность и не потребляет от него реактивную мощность вообще. Такой режим цепи называют резонансом напряжений.
|
|
|
Для получения режима полной компенсации рассчитать и установить значение величины индуктивности. Поскольку, падения напряжения на катушке индуктивности и напряжения на конденсаторе должны быть равны, то должны быть равны и их сопротивления: 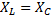 .
.
Определить емкостное и полное сопротивление:


Определить значение величины индуктивности L, учитывая что 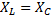 , а
, а  Рассчитанные значения
Рассчитанные значения  занести в таблицу 1.4, строка 1.
занести в таблицу 1.4, строка 1.
Таблица 1.4 - Данные опытов и расчетов
| № пп | U,В | f, Гц | U 1, В | U 2, В | I, А | P, Вт | cosφ | cosφ | φ, град | R, Ом | XL , Ом | XC , Ом | Q, BAр | S, BA |
| Данные опытов | Результаты расчетов | |||||||||||||
Установим рассчитанное значение величины индуктивности на схеме.
Включить схему в сеть. Результаты опыта приведены на рисунке 1.6.
Пронаблюдать на экране осциллографа совмещение осциллограмм входного напряжения и тока в цепи;
Измерить действующие значения входного напряжения U, тока в цепи I, напряжение на индуктивной катушке UL и на конденсаторе UC, активную мощность, потребляемую в цепи P, коэффициент мощности cosφ. Данные опытов занести в таблицу 1.4, строка 1.

Рисунок 1.6 - Распределение тока цепи, падений напряжений на элементах, активная мощность (слева) и осциллограммы напряжения источника и тока цепи в резонансном режиме
По данным опыта видно, что индуктивное и емкостное падения напряжения уравновешивают друг друга, а напряжение на резисторе в точности равно действующему значению напряжения источника.
Осциллограммы напряжения источника и тока цепи (рисунок 1.6) в резонансном режиме совпадают по фазе, угол сдвига  , следовательно, коэффициент мощности цепи в целом
, следовательно, коэффициент мощности цепи в целом  .
.
Уравнения мгновенных значений напряжений и токов, описывающие кривые на осциллограмме:
 ;
;

Поскольку полная мощность  , а индуктивная мощность равна емкостной мощности
, а индуктивная мощность равна емкостной мощности  то
то 
|
|
|
С другой стороны, активная мощность  , а
, а 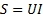 , т.е.
, т.е. 
Цепь в режиме резонанса напряжений не потребляет от источника реактивной мощности, а полная мощность, потребляемая всей цепью, равна активной.
Рассчитать коэффициент мощности цепи cosφ и фазовый угол φ. Полученные расчеты занести в таблицу 1.1.
Реактивные мощности катушки и конденсатора равны, то цепь потребляет от источника только активную мощность, а коэффициент мощности равен единице.
Построить векторную диаграмму по результатам опыта. На рисунке 1.4 б представлена векторная диаграмма цепи в режиме полной компенсации реактивной мощности.
Геометрическая сумма векторов падений напряжений на элементах электрической цепи переменного тока равен вектору приложенного напряжения:

Вектор падения напряжения на активном сопротивлении равен вектору напряжения источника и совпадает по фазе с ним и с вектором тока. Векторы падений напряжений на реактивных сопротивлениях уравновешивают друг друга.
5.3.2 Эксперимент 2
Расстроить резонансный режим уменьшив индуктивность дросселя клавишей SHIFT + С. Включить схему в сеть. Результаты опыта приведены на рисунке 1.6.
Снять осциллограммы напряжения источника и тока цепи и повторить все измерения.

Рисунок 1.7 - Распределение тока цепи, падений напряжений на элементах, активная мощность (слева) и осциллограммы напряжения сети и тока цепи при L =5 % от 50 мГн
Измерить действующие значения входного напряжения U, тока в цепи I, напряжение на индуктивной катушке UL и на конденсаторе UC, активную мощность, потребляемую в цепи P, коэффициент мощности cosφ. Данные опытов занести в таблицу 1.4, строка 2.
На осциллограмме видно, что кривая тока цепи сдвинута по отношению к кривой напряжения источника на угол 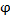 (рисунок 1.7).
(рисунок 1.7).
Уравнения мгновенных значений напряжений и токов, описывающие кривые на осциллограмме:
 .
.
Полная мощность, потребляемая цепью:
Коэффициент мощности:
 или
или 
Цепь потребляет от источника активную мощность:
 ;
;
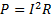 ;
;
или
 .
.
Реактивная мощность равна разности индуктивной и емкостной мощностей:
|
|
|

или 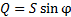 .
.
Коэффициент мощности:

Полная мощность:
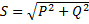 ,
,
а для цепи, содержащей конденсатор и катушку индуктивности:
 .
.
Тогда для коэффициента мощности такой цепи:

Реактивная мощность конденсатора больше реактивной мощности катушки, то цепь потребляет от источника активную мощность и отдает в сеть избыточную реактивную.
Построить векторную диаграмму по результатам опыта. На рисунке 1.4 в представлена векторная диаграмма цепи в режиме частичной компенсации реактивной мощности.
5.3.3 Эксперимент 3
Расстроить резонансный режим увеличив индуктивность дросселя. Включить схему в сеть. Результаты опыта приведены на рисунке 1.8.
Снять осциллограммы напряжения источника и тока цепи и повторить все измерения.
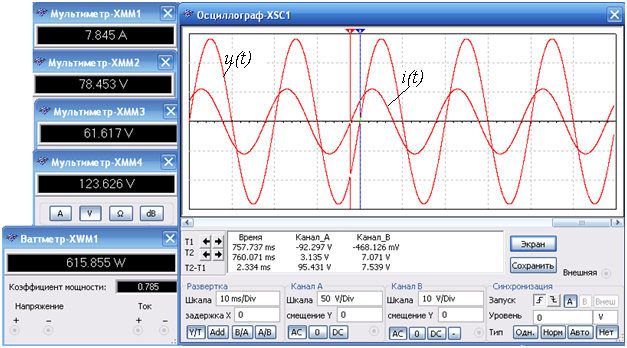
Рисунок 1.8- Распределение тока цепи, падений напряжений на элементах, активная мощность (слева) и осциллограммы напряжения сети и тока цепи при L =50 % от 50 мГн
Измерить действующие значения входного напряжения U, тока в цепи I, напряжение на индуктивной катушке UL и на конденсаторе UC, активную мощность, потребляемую в цепи P, коэффициент мощности cosφ. Данные опытов занести в таблицу 1.4, строка 3.
На осциллограмме видно, что кривая тока цепи сдвинута по отношению к кривой напряжения источника на угол 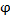 (рисунок 1.7).
(рисунок 1.7).
Уравнения мгновенных значений напряжений и токов, описывающие кривые на осциллограмме:


Построить векторную диаграмму по результатам опыта. На рисунке 1.4 а представлена векторная диаграмма цепи в режиме перекомпенсации реактивной мощности.
Реактивная мощность катушки больше реактивной мощности конденсатора, то цепь потребляет от источника и активную, и реактивную мощность.
Сделать выводы
Контрольные вопросы
1 Что такое емкостное и индуктивное сопротивления цепи? От чего они зависят?
2 Почему при последовательном соединении катушки индуктивности и конденсатора напряжения на них могут оказаться больше входного напряжения?
3 Что такое резонанс напряжений?
4 Изменением каких параметров цепи можно получить режим резонанса напряжений?
5 С помощью каких приборов можно определить резонансный режим?
ЛАБОРАТОРНАЯ РАБОТА № 2
Исследование линейной цепи синусоидального тока при параллельном соединении активно-индуктивного приемника и батарей конденсаторов
Цель работы: Экспериментально исследовать условия возникновения резонанса токов и возможности его применения для повышения коэффициента мощности электрических установок; определить параметры цепи по результатам измерений в различных режимах; проанализировать режим резонансов токов.
|
|
|
1 Программа работы
1.1 Ознакомиться со схемой установки (рис.2.1) и измерительными приборами. Записать данные приборов и их типы.
Рисунок 2.1- Принципиальная схема исследуемой цепи
1.2 В цепи (рис.2.1):
- отключить батарею конденсаторов;
- подключить осциллограф для снятия осциллограмм входного напряжения и тока. На вход Х осциллографа подать напряжение с шунта Rш, а на вход Y – входное напряжение;
- включить цепь тумблером F;
- снять осциллограмму тока i и напряжения u вх; измерить действующие значения напряжения U вх, тока в цепи I (показания амперметров А и А 1 будут одинаковы) и активную мощность P, потребляемую в цепи. Данные измерений занести в таблицу 2.1, строка 1.
Рассчитать cosφи фазовый угол сдвига между током и напряжением. Данные расчетов внести в таблицу 2.1.
1.3 Подключить батарею конденсаторов. Увеличивая емкость батареи (дискретно с интервалом 0,5мкФ) с помощью тумблеров F 2- F 7, настроить цепь в резонанс, наблюдая на экране осциллографа совмещение осциллограмм входного напряжения u вх и тока i. Снять осциллограмму тока и напряжения в резонансном режиме. Измерить действующее значение напряжения U и токов I, I 1, I 2, а также активную мощность потребляемую в цепи. Данные опытов внести в таблицу 2.1.
1.4 Расстроить резонансный режим двумя способами - один раз уменьшив ёмкость батареи конденсаторов, адругой раз увеличив её. Снять осциллограммы и повторить все измерения и расчеты п. 1.3, для этих режимов. Данные опытов занести в таблицу 2.1.
1.5 Рассчитать коэффициент мощностиcosφ и фазовый угол сдвига φна входе цепи для всех трех режимов (φ>0; φ=0; φ<0).Данные расчетов внести в таблицу 2.1. Построить векторные диаграммы токов и напряжений.
1.6 Выполнить исследование заданной цепи виртуально с помощью программы Multisim 10.
Таблица 2.1-Данные опытов и расчетов
| № пп. | U, В | f, Гц | C,мкФ | P,Вт | I,А | I 1,Ом | I 2,А | cosφ | φ, град | ||
| Данные опытов | Результаты расчетов | ||||||||||
2 Пояснения к работе
При подключении параллельно к активно-индуктивному приемнику батареи конденсаторов в цепи можно получить резонанс токов.
Резонанс токов – это такой режим цепи переменного тока с параллельно соединенными с индуктивностью и емкостью, при котором ток в неразветвленной части цепи I совпадает по фазе с напряжением U.
Реактивные составляющие токов в параллельных ветвях равны по величине и противоположны по фазам. Ток в неразветвленной части цепи  минимален, равен активной составляющей тока катушки и может быть значительно меньше по величине, чем ток в параллельных ветвях.
минимален, равен активной составляющей тока катушки и может быть значительно меньше по величине, чем ток в параллельных ветвях.
Реактивная мощность от источника не потребляется, хотя индуктивная и емкостная мощности существуют и могут иметь большие значения. Объясняется это тем, что при резонансе происходит непрерывный обмен реактивной энергии между потребителем и батареей конденсаторов.
При резонансе от источника потребляется лишь активная мощность, т.е.  .
.
Коэффициент мощности  .Ток и напряжение во входной цепи совпадают по фазе - именно этот факт имеет исключительно важное значение для практического применения.
.Ток и напряжение во входной цепи совпадают по фазе - именно этот факт имеет исключительно важное значение для практического применения.
3 Описание лабораторной установки
На панели стенда собрана цепь рисунок 2.1, состоящая из индуктивной катушки и батареи конденсаторов с регулируемой емкостью. Для измерения токов и напряжения используются амперметр и вольтметр электромагнитной системы или мультиметр. Активная мощность измеряется ваттметром электродинамической системы. Для исследования амплитудно–фазовых соотношений используется двух лучевой осциллограф С–1-49.
4 Методические указания
1 Для осциллографирования тока на вход Х осциллографа подается напряжение, снятое с малого сопротивления Rш, включенного в неразветвленную часть цепи.
Градуировку осциллограммы тока проще всего производить следующим образом: по показаниям амперметра вычислить амплитуду тока, А:
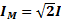 ,
,
где I – действующее значение тока (показания амперметра).
Масштаб тока А/мм на экране осциллографа 
Масштаб напряжения В/мм определяется аналогично: 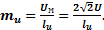 Здесь U вх – показания вольтметра, lu – двойная амплитуда синусоидального напряжения.
Здесь U вх – показания вольтметра, lu – двойная амплитуда синусоидального напряжения.
Режим резонанса удобно фиксировать по совпадению моментов переход через ноль синусоидального тока и напряжения на входе цепи, как показано на рисунке 2.2.
Рисунок 2.2- К определению масштаба тока на осциллограмме
Коэффициент мощности цепи
Отсюда


Знак угла φ для каждого режима определяется по осциллограмме. Величину угла φ также можно определить по осциллограмме. Для этого нужно определить соотношение  (рис. 2.3, б, в), при помощи линейки. Далее, зная, что
(рис. 2.3, б, в), при помощи линейки. Далее, зная, что  (электрических градусов) найти фазовый угол сдвига
(электрических градусов) найти фазовый угол сдвига
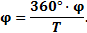
а) б) в)
Рисунок 2.3 Временные диаграммы тока в цепи и напряжения на входе цепи: а) φ=0, ток и напряжение совпадают по фазе; б) φ>0, ток отстает от напряжения; в) φ<0, ток опережает
· Основными потребителями электрической энергии являются асинхронные двигатели, представляющие собой активно-индуктивную нагрузку. Их подключение к сети соответствует векторной диаграмме (рис. 2.4,а). Построение диаграммы целесообразно начинать с вектора  , приняв начальную фазу его равной нулю. Ток I в подводящих проводах и в нагрузке будет один и тот же, он отстает по фазе от напряжения на уголφ.
, приняв начальную фазу его равной нулю. Ток I в подводящих проводах и в нагрузке будет один и тот же, он отстает по фазе от напряжения на уголφ.
При подключении батареи конденсаторов во второй ветви появляется ток, величина которого зависит от входного напряжения и емкостного сопротивления батареи конденсаторов:

По фазе ток на конденсаторе, как известно, опережает напряжение на 90о. Вектор тока İС при различных сопротивлениях показан на рисунке 2.4(б,в,г).
Рисунок2.4- Векторные диаграммы смешанной цепи R,L,C при постоянной частоте и индуктивности и переменной ёмкости
Наибольший интерес представляет такой режим работы цепи, когда емкостной ток İC равен по величине индуктивной составляющей тока İL. Ток в подводящих проводах  будет равен в этом случае активной составляющей тока IR. Режим работы приемника при подключении батареи конденсаторов не изменился (
будет равен в этом случае активной составляющей тока IR. Режим работы приемника при подключении батареи конденсаторов не изменился ( ), но условия работы сети улучшились – ток в подводящих проводах уменьшился, коэффициент мощности цепи увеличился (
), но условия работы сети улучшились – ток в подводящих проводах уменьшился, коэффициент мощности цепи увеличился (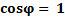 ), так как ток
), так как ток  и напряжение
и напряжение  совпадают по фазе. В параллельных ветвях происходит обмен электромагнитной энергией между конденсатором и катушкой индуктивности, энергия как бы пульсирует, переходя два раза за период из индуктивной катушки в конденсатор и обратно. На внешнюю цепь этот процесс обмена энергией влияния не оказывает, поэтому вся установка ведет себя как потребитель активной мощности.
совпадают по фазе. В параллельных ветвях происходит обмен электромагнитной энергией между конденсатором и катушкой индуктивности, энергия как бы пульсирует, переходя два раза за период из индуктивной катушки в конденсатор и обратно. На внешнюю цепь этот процесс обмена энергией влияния не оказывает, поэтому вся установка ведет себя как потребитель активной мощности.
На рисунке 2.4(в, г) показаны векторные диаграммы при недокомпенсации (в) и перекомпенсации (г) сдвига фаз между током и напряжением. В случае недокомпенсации емкостный ток İC меньше реактивной составляющей тока индуктивной катушки. В этом случае будет иметь место фазовый угол сдвига φ между током и напряжением, коэффициент мощности цепи cosφуже не будет равен единице, хотя несколько увеличится. В случае перекомпенсации, когда İC>İL, ток в подводящих проводах İ будет опережать напряжение по фазе (рисунке 2.4,г). В этих двух случаях в обмене электромагнитной энергией участвуют не только конденсатор и индуктивная катушка, но и источник энергии.
|
|
|


