Главная | Обратная связь | Поможем написать вашу работу!

Определение синуса, косинуса и тангенса острого угла прямоугольного треугольника

Введение

Математика является неотъемлемой и существенной частью общечеловеческой культуры. Изучение данной дисциплины оказывает значительное воздействие на развитие и формирование личности, совершенствует мышление, помогает выработке мировоззрения, качественно влияет на нравственное и духовное воспитание учащихся. Эффективность обучения во многом зависит от подбора задач, от их систематизации. В современной методике обучения математике все больше внимания уделяется использованию совокупностей, систем задач.

Тригонометрия традиционно является одной из важнейших составных частей школьного курса математики, представляет собой его целостный и самостоятельный раздел. Даже при первоначальном знакомстве с тригонометрией обращает на себя внимание тот факт, что этот предмет тесно связан с геометрией, а значит и с решением задач, что всегда вызывают особые трудности у учащихся. Решение же задач с применением тригонометрии еще более усиливает эти трудности.

Сейчас все большее распространение получает прогрессивный метод обучения через задачи как реализация системы проблемного обучения. Задачи становятся не только и не столь целью, сколько средством обучения. Умение решать задачи - показатель обученности и развития учащихся. Умение решать задачи с помощью тригонометрии показатель высокой культуры ученика.

Несмотря на то, что задачи в 8 классе курса геометрии решаются в большом количестве, затем тригонометрия используется и при решении задач в курсе алгебры, это остается проблемой для всех учащихся. Они часто заменяют простой тригонометрический метод решения задач более сложным геометрическим или алгебраическим.

Подобная тенденция, к сожалению, сохраняется и в последние годы. Необходимы поиски путей устранения данной проблемы, что свидетельствует об актуальноститемы нашего исследования.

Объект исследования: задачи по геометрии с применением тригонометрии в курсе математики 8 класса.

Предмет исследования: методика решения задач по геометрии с применением тригонометрии в 8 классе.

Цель исследования: изучить различные методические подходы к решению задач по геометрии с применением тригонометрии в курсе математики 8 класса.

Гипотеза исследования: оптимальный подход к решению задач по геометрии с применением тригонометрии будет способствовать развитию аналитического, логического, конструктивного мышления учащихся и формированию их математической зоркости.

Методы исследования: наблюдение, анализ, сравнение, репродуктивный и частично - поисковый.

Задачи исследования:

Глубоко изучить тригонометрический материал в курсе геометрии основной школы;

- Рассмотреть различные методы решения текстовых задач, предлагаемых альтернативных учебниках;

- Решить наиболее интересные задачи из курса геометрии 8 класса;

- Рассмотреть нестандартные задачи, предлагаемые в альтернативных учебниках геометрии;

- Проверить гипотезу.

Глава 1. Соотношение между сторонами и углами прямоугольного треугольника в курсе геометрии 8 класса

История развития вопроса

История тригонометрии, как науки о соотношениях между углами и сторонами треугольника и других геометрических фигур, охватывает более двух тысячелетий. Большинство таких соотношений нельзя выразить с помощью обычных алгебраических операций, и поэтому понадобились ввести особые тригонометрические функции, первоначально оформлявшиеся в виде числовых таблиц.

Историки полагают, что тригонометрию создали древние астрономы, немного позднее её стали использовать в геодезии и архитектуре. Со временем область применения тригонометрии постоянно расширялась, в наши дни она охватывает практически все естественные науки, технику и ряд других областей деятельности.

Фундаментальное изложение тригонометрии как самостоятельной науки (как плоской, так и сферической) дал персидский математик и астроном Насир ад-Дин ат-Туси в 1260 году. Его «Трактат о полном «четырёхстороннике» содержит практические способы решения типичных задач, в том числе труднейших, решенных самим ат-Туси - например, построение сторон сферического треугольника по заданным трём углам. Сочинение ат-Туси стало широко известно в Европе и существенно повлияло на развитие тригонометрии.

Таким образом, к концу XIII века были открыты базовые теоремы, составляющие содержание тригонометрии:

Выражение любой тригонометрической функции через любую другую;

Формулы для синусов и косинусов кратных и половинных углов, а также для суммы и разности углов;

Теоремы синусов и косинусов;

Решение плоских и сферических треугольников.

Современный вид тригонометрии придал Леонард Эйлер. В трактате «Введение в анализ бесконечных» (1748) Эйлер дал определение тригонометрических функций, эквивалентное современному, и соответственно определил обратные функции. Если его предшественники понимали синус и прочие понятия геометрически, то есть как линии в круге или треугольнике, то после работ Эйлера, стали рассматриваться как безразмерные аналитические функции действительного и комплексного переменного. Для комплексного случая он установил связь тригонометрических функций с показательной функцией (формула Эйлера). Подход Эйлера с этих пор стал общепризнанным и вошёл в учебники.

В России первые сведение о тригонометрии были опубликованы в сборнике «Таблицы логарифмов, синусов и тангенсов к изучению мудролюбивых тщателей», опубликованном при участии Л.Ф. Магницкого в 1703 году.

В 1714 году появилось содержательное руководство «Геометрия практика», первый русский учебник по тригонометрии, ориентированный на прикладные задачи артиллерии, навигации и геодезии. Завершением периода освоения тригонометрических знаний в России можно считать фундаментальный учебник академика М.Е. Головина (ученика Эйлера) «Плоская и сферическая тригонометрия с алгебраическими доказательствами» (1789).

Определение синуса, косинуса и тангенса острого угла прямоугольного треугольника

Рассмотрим прямоугольный треугольник АВС с прямым углом С (рис. 1).

Рис.1

Катет ВС этого треугольника является противолежащим углу А, а катет АС - прилежащим к этому углу.

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

Синус, косинус и тангенс угла α обозначаются символами sin α, cos α, tg α (читаются: «синус альфа», «косинус альфа» и «тангенс альфа». На рисунке 1

sin А = , (1)

cos А = (2)

tg А = . (3)

Из формул (1) и (2) получаем:

= * =

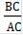
Сравнивая с формулой (3), находим:

tg А= (4),

то есть тангенс угла равен отношению синуса к косинусу этого угла.

Докажем, что если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны. В самом деле, пусть АВС и А₁В₁С - два прямоугольных треугольника с прямым углами С и С₁ и равными острыми углами А и А₁. Треугольники АВС и А₁В₁С₁ подобны по первому признаку подобия треугольников, поэтому = = . Из этих равенств следует, что = , то есть sin А = sin А₁. Аналогично = , то есть cos А = cos А₁, и = , то есть tg А = tg А₁.