 |
Основное тригонометрическое тождество в курсе геометрии 8 класса
|
|
|
|
Докажем теперь справедливость равенства
 +
+  = 1
= 1
Возьмем любой прямоугольный треугольник АВС с углом при вершине А, равным α (рис. 3).
В
 А
А
С
Рис. 3
По теореме Пифагора  +
+  =
=  . Разделим обе части равенства на
. Разделим обе части равенства на  . Получим:
. Получим:
 +
+  = 1, sin А =
= 1, sin А =  , cos А =
, cos А =  .
.
Таким образом,  α +
α +  α = 1 (1).
α = 1 (1).
Это равенство есть тождество. Оно верно для любого острого угла α.
 α +
α +  α = 1
α = 1
называется основным тригонометрическим тождеством.
Из основного тригонометрического тождества можно получить два тождества:
1 +  α =
α = 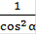 (2) и 1 +
(2) и 1 +  α =
α =  (3).
(3).
Чтобы получить второе тождество, разделим обе части полученного равенства на  α. Получим:
α. Получим:
 + 1 =
+ 1 = 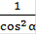 , или 1 +
, или 1 +  α =
α = 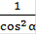 (4)
(4)
Если обе части тождества  α +
α +  α = 1 разделить на
α = 1 разделить на  α, то получим третье тождество:
α, то получим третье тождество:
1 +  α =
α =  (5).
(5).
Значение этих тождеств заключается в том, что они позволяют, зная одну из величин  α или
α или  α, найти две другие.
α, найти две другие.
Примером применения этих тождеств может служить такая задача:
Вычислите значения sin α и  α, если
α, если  α =
α =  , где α - острый угол.
, где α - острый угол.
Решение:
Так так  α +
α +  α = 1, то sin α =
α = 1, то sin α =  =
=  =
=  ,
,
 =
=  =
= 
Ответ: sin α =  ,
,  =
=  .
.
1.4 Значения синуса, косинуса и тангенса для углов 30˚, 45˚ и 60˚
Найдем сначала значение синуса, косинуса и тангенса для углов 30˚ и 60˚. Для этого рассмотрим прямоугольный треугольник АВС с прямым углом С (рис. 4), у которого ∟А=30˚, ∟В =60˚.
В
 А
А
С
Рис.4
Так как катет, лежащий против угла в 30˚, равен половине гипотенузы, то  =
=  . Но
. Но  = sin А = sin 30˚. С другой стороны,
= sin А = sin 30˚. С другой стороны,  =
=  В =
В =  60˚. Итак, -sin 30˚ =
60˚. Итак, -sin 30˚ =  ,
,  60˚ =
60˚ =  . Из основного тригонометрического тождества получаем:
. Из основного тригонометрического тождества получаем:
 30˚ =
30˚ =  =
=  =
=  ,
,
 =
=  =
=  =
=  .
.
|
|
|
По формуле (4) находим:
tg 30˚ =  =
=  =
=  , tg 60˚ =
, tg 60˚ =  =
= 
Найдем теперь sin 45˚,  45˚ и tg 45˚. Для этого рассмотрим равнобедренный прямоугольный треугольник АВС с прямым углом С (рис. 5).
45˚ и tg 45˚. Для этого рассмотрим равнобедренный прямоугольный треугольник АВС с прямым углом С (рис. 5).
А
 В
В
С
Рис. 5
В этом треугольнике АС = ВС, ∟А=∟В= 45˚. По теореме Пифагора
 =
=  +
+  = 2
= 2  = 2
= 2  , откуда АС = ВС =
, откуда АС = ВС =  .
.
Следовательно,
sin 45˚ =  =
=  =
=  =
=  ,
,  45˚=
45˚= 
 =
=  =
=  =
=  ,
,
tg 45˚= tg  =
=  = 1.
= 1.
Составим таблицу значений sin α,  α и
α и  для углов α, равных 30˚, 45˚ и 60˚:
для углов α, равных 30˚, 45˚ и 60˚:

| 30˚ | 45˚ | 60˚ |

| 
| 
| 
|

| 
| 
| 
|
| tg α | 
| 1 | 
|
Для любого острого угла α справедливы равенства:
 (90˚ - α) =
(90˚ - α) =  α
α
 (90˚ - α) =
(90˚ - α) =  α
α
Пусть АВС - прямоугольный треугольник с острым углом α при вершине А (рис. 6). Тогда острый угол при вершине В равен 90˚ - α. По определению
sin А =  , cos А =
, cos А =  ,
,
 (90˚ - α) =
(90˚ - α) =  ,
,  (90˚ - α) =
(90˚ - α) =  .
.
Из этого следует, что  (90˚ - α) =
(90˚ - α) =  α и
α и  (90˚ - α) =
(90˚ - α) =  α.
α.
В
 А
А
С
Рис.6
аналитический математический геометрия тригонометрия
Глава 2. Задачи по геометрии с применением тригонометрии в курсе геометрии 8 класса
Задачи на вычисление
Роль задач по тригонометрии в геометрии очень велика, так как решение задач с конкретным содержанием помогает осуществлять постепенный переход к дедуктивным доказательствам. Систематическое решение задач способствует сознательному и прочному усвоению теории, помогает увидеть ее практическую ценность, в то же время решение задач развивает логическое мышление ученика, творческую инициативу, сообразительность и дает ему ряд нужных практических умений и навыков. Самое главное, что знание тригонометрии способствует экономии рабочего времени ученика во многих ситуациях.
Рассмотрим задачи на вычисление.
Задача 1
Найти синус, косинус и тангенс угла А треугольника АВС с прямым углом С, если ВС = 8, АВ = 17.
A
 В
В
С
Дано: Δ ABC, ∟С = 90˚.
Найти: sin А, cos А, tg А.
|
|
|
Решение:
Так как Δ АВС прямоугольный, то теореме Пифагора АС = 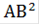 -
-  ,
,
АС =  = 15
= 15
sin А =  , sin А =
, sin А =  ,
,
cos А =  , cos А =
, cos А =  ,
,
tg А =  , tg А =
, tg А = 
Ответ: sin А =  , cos А =
, cos А =  , tg А =
, tg А =  .
.
Такие задачи способствуют осознанному восприятию определения синуса, косинуса и тангенса острого угла прямоугольного треугольника.
Задача 2
Найти площадь равнобедренной трапеции с основаниями 2 см и 6 см, если угол при большем основании равен α.
А D
 В
В
В1 С1 С
Дано: ABCD - трапеция, АВ = СD, ВС = 2 см, АD = 6 см, ∟А = α.
Найти: SАВСD.
Решение:
) Рассмотрим прямоугольные треугольники АВВ1 и DСС1.
Δ АВВ1 = Δ ДСС1 по катету и гипотенузе (АВ = СD по условию, ВВ1 = СС1 как расстояния между параллельными прямыми ВС и АD), из этого следует, что АВ1 = С1D как соответственные элементы равных треугольников. А В1 = С1 D = (6 - 2): 2 = 2 см.
) Рассмотрим Δ АВВ1:
ВВ1 = А В1 * tg ∟А, ВВ1 = 2 * tg α.
3) SАВСD =  (АД + ВD) * ВВ1
(АД + ВD) * ВВ1
SАВСD =  (6 + 2) * 2 tg α = 8 tg α
(6 + 2) * 2 tg α = 8 tg α  .
.
Ответ: SАВСD = 8 tg α  .
.
Задача 3
Найти диагонали ромба, если его диагонали равны 2  и 2.
и 2.
А В

D С
Дано: АВСD - ромб, АС = 2, ВD = 2  .
.
Найти: ∟А, ∟В.
Решение:
) Рассмотрим Δ АОВ, АО =  АС, ВО =
АС, ВО =  ВD по свойству диагоналей ромба,
ВD по свойству диагоналей ромба,
АО =  * 2 = 1, ВО =
* 2 = 1, ВО =  * 2
* 2  =
= 
2) Δ АОВ - прямоугольный, ∟О = 90˚.
tg∟ВАО =  , tg∟ВАО =
, tg∟ВАО =  =
=  , значит, ∟ВАО = 60˚,
, значит, ∟ВАО = 60˚,
∟АВО = 90˚ - 60˚= 30˚
) ∟А = 60˚ * 2 = 120˚, ∟В = 30˚ * 2 = 60˚ по свойству ромба,
∟С = 180˚ - 60˚ = 120˚, ∟D = 180˚ - 120˚ = 60˚,
так как сумма односторонних углов равна 180˚
Ответ: ∟А = ∟В =120˚, ∟В = ∟D = 60˚.
Решение таких задач способствует не только осознанному закреплению определений синуса, косинуса и тангенса острого угла прямоугольного треугольника, но и развитию математической зоркости учащихся.
Задача 4
В параллелограмме АВСD сторона равна 12 см, а угол ВАD равен 47˚50̛. Найти площадь параллелограмма, если его диагональ ВD перпендикулярна к стороне АВ.
D С

А В
Дано: АВСD - параллелограмм, АD = 12, ∟ВАD = 47˚50̛, ВD АВ.
Найти: SАВСD.
Решение:
) Рассмотрим Δ АВD, он прямоугольный, ∟= 90˚
2)  = cos∟ А, АВ = АD * cos∟ А
= cos∟ А, АВ = АD * cos∟ А
АВ = 12 * cos 47˚50̛ = 12 * 0, 6712 ≈ 8,06
 = sin ∟ А, ВD = АD * sin ∟ А
= sin ∟ А, ВD = АD * sin ∟ А
|
|
|
ВD = 12 * sin 47˚50̛ = 12 * 0, 7412 ≈ 8,89
) SАВСД = АВ * ВD, SАВСD = 8,06 * 8,89 ≈ 71,76 ≈ 72
Ответ: 72
Решение подобных задач способствует формированию у учащихся умений рассуждать, связывать воедино вопросы алгебры, геометрии, тригонометрии.
Задача 5
Стороны прямоугольника равны 3 см и  см. Найти углы, которые образует диагональ со стороной прямоугольника.
см. Найти углы, которые образует диагональ со стороной прямоугольника.
В С

А D
Дано: АВСD - прямоугольник, АВ =  , АD = 3.
, АD = 3.
Найти: ∟АВD, ∟АDВ.
Решение:
) Рассмотрим Δ АВD - прямоугольный, так как ∟А = 90˚,
tg ∟ АВD =  , tg ∟ АВD =
, tg ∟ АВD =  =
=  , ∟ АВD = 60˚,
, ∟ АВD = 60˚,
∟АDВ = 90˚ - 60˚ = 30˚
Ответ: ∟ АВD = 60˚, ∟АDВ = 30˚.
Решение такой задачи способствует развитию исследовательских навыков у учащихся. Например, при решении этой задачи ученик должен увидеть прямоугольный треугольник, выяснить какими углами являются ∟АВД и ∟АДВ, вспомнить определение синуса, косинуса, тангенса, выбрать необходимые определения. Еще более глубокие исследования проводит ученик, решая следующую задачу:
Задача 6
В равнобедренный треугольник РМК с основанием МК вписана окружность с радиусом 2  . Высота PH делится точкой пересечения с окружностью в отношении 1: 2, считая от вершины Р. Найти периметр треугольника РМК и установить его вид.
. Высота PH делится точкой пересечения с окружностью в отношении 1: 2, считая от вершины Р. Найти периметр треугольника РМК и установить его вид.
N
 Р
Р
М Н К
Дано: Δ РМК - равнобедренный, МК - основание, окр. (О; r) - вписана, РН - высота, РА: АН = 1: 2, r = 2  .
.
Найти: РРМК.
Решение:
) Так как РА: АН = 1: 2, тот НА = 2РА, то есть РН = 3ОА = 3 ОН = 3РА, так как ОА = 2  , то РН = 6
, то РН = 6  .
.
2) Рассмотрим Δ МРН: ∟РНМ = 90˚, так как РН - высота,
sin ∟М =  , отсюда РМ =
, отсюда РМ =  , РН = 6
, РН = 6  .
.
Δ ОРМ - прямоугольный, так как ОN РМ, где N - точка касания по свойству касательных к окружности.
Значит, sin ∟ NРО =  , sin ∟ NРО =
, sin ∟ NРО =  =
=  , ∟ NРО = 30˚, значит, ∟М = 60˚.
, ∟ NРО = 30˚, значит, ∟М = 60˚.
Следовательно,
РМ =  =
=  = 12
= 12
3) Так как Δ МРК - равнобедренный, ∟М = 60˚ (угол при основании), то Δ МРК - равносторонний.
Значит, МР = РК = МК = 12.
) РРМК = 36.
|
|
|
Ответ: 36, треугольник равносторонний.
Интересной задачей для учеников 8 класса является задача на вычисление высоты и площади правильного треугольника.
Задача 7
Найти высоту и площадь правильного треугольника со стороной а и высотой h.
Дано: Δ АВС - правильный, АВ = ВС = АС = а, BD = h - высота.
Найти: SАВС, h.
А
 В
В
D С
Решение:
) Рассмотрим прямоугольный треугольник АВD (так как BD - высота). Из прямоугольного треугольника АВD находим BD = АВ * sin 60˚.
BD = h = а *  =
= 
2) SАВС =  , SАВС =
, SАВС =  =
= 
Ответ: h =  , SАВС =
, SАВС =  .
.
Как видим, задача очень легко и быстро решается с помощью тригонометрии.
При этом развивается не только аналитическое, логическое мышление учащихся, их математическая зоркость, но и умение рационально мыслить, экономить свое рабочее время, находить оптимальные пути решения задач.
Для сравнения покажем, как задача решалась до изучения вопросов тригонометрии.
Дано: Δ АВС - правильный, АВ = ВС = АС = а, BD = h - высота.
Найти: SАВС, h.
Решение:
1) Проводим высоту BD.
2) Δ АВD: ∟ВАD = 60˚, тогда ∟АВD = 30˚, а против угла в 30˚ лежит
АD =  АВ, АD =
АВ, АD =  .
.
3) BD = h = 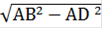 , BD = h =
, BD = h =  =
=  =
= 
4) SАВС =  , SАВС =
, SАВС =  =
= 
Ответ: h =  , SАВС =
, SАВС =  .
.
Затруднения, которые испытывают при решении подобных задач ученики, вызываются не геометрическим содержанием, а скорее непривычкой учащихся применять в геометрии свои знания по тригонометрии.
Задачи, для решения которых должны быть использованы многие геометрические предложения, требующие умения разобраться в чертежах, установить связь между данными и искомыми элементами, провести ряд умозаключений для обоснования своих догадок. Такие задачи расширяют геометрические представления учащихся, их пространственное воображение, развивают логическое мышление, способствуют межпредметной интеграции.
Задачи на построение
Задача на построение состоит в том, что требуется построить наперед указанными инструментами некоторую фигуру, если дана некоторая другая фигура и указаны некоторые соотношения между элементами искомой фигуры и элементами данной фигуры.
Каждая фигура, удовлетворяющая задаче, называется решением этой задачи. Найти решение задачи на построение - значит свести ее к конечному числу основных построений, то есть указать конечную последовательность основных построений.
Задача 1
Построить угол α в прямоугольном треугольнике АВС, если известно, что tg α =  .
.
Эта задача, как и любая другая на построение, требует глубокого анализа.
Учитель должен приучить учеников задавать себе вопросы следующего характера:
|
|
|
Что должно выполняться в этом треугольнике, если tg α =  ?
?
(Так как tg А =  , то на ВС приходится три единицы, а на АС - пять единиц).
, то на ВС приходится три единицы, а на АС - пять единиц).
Дано: tg α =  .
.
Построить: ∟α.
Решение:
Задача решается путем построения прямоугольного треугольника по двум катетам, тангенс α - это отношение противолежащего катета к прилежащему катету. Из условия следует, что противолежащий катет равен 3, а прилежащий равен 5. Строим прямоугольный треугольник с катетами три единицы и пять единиц:
А
 В
В
С
Задача 2
Построить в прямоугольном треугольнике угол, синус которого в два раза больше его косинуса.
Дано: sin α = 2 cos α.
Построить: угол α.
Решение: Пусть α - искомый угол. По условию sin α = 2 cos α, отсюда tg α = 2.Поэтому необходимо построить прямоугольный треугольник с прямым углом С, у которого  =
=  . Тогда ∟А будет искомым.
. Тогда ∟А будет искомым.
 ВС
ВС
Систематическое изучение геометрических построений необходимо в школьном курсе, так как в процессе изучения задач они концентрируют в себе знания из других областей математики, развивают навыки практической графики, формируют поисковые навыки решения практических проблем, приобщают к посильным самостоятельным исследованиям, способствуют выработке конкретных геометрических представлений, а также к более тщательной обработке умений и навыков.
Задачи на доказательство
В задачах на доказательство требуется обосновать некоторые утверждение относительно геометрической фигуры, которое высказано заранее. Решение задач на доказательство имеет большое значение в развитии логической мысли учащихся. Именно при выполнении доказательств оттачивается логическое мышление учеников, разрабатываются логические схемы решения задач, возникает потребность учащихся в обосновании математических фактов. Это можно увидеть при решении следующей задачи:
Задача 1
В прямоугольном треугольнике синус угла А равен  . Доказать, что косинус угла В равен
. Доказать, что косинус угла В равен  , ∟ С = 90˚.
, ∟ С = 90˚.
Решение: Рассмотрим прямоугольный треугольник АВС (∟С = 90˚):
А
 ВС
ВС
На основе определения sin А =  , а cos А =
, а cos А =  .
.
sin A = cos B, так как ∟А + ∟В = 90˚, то ∟В = 90˚ - ∟А,
cos B = cos(90˚ - ∟А) = sin A, sin A =  30˚, B = cos(90˚ - 30˚) = cos 60˚ =
30˚, B = cos(90˚ - 30˚) = cos 60˚ =  , что и требовалось доказать.
, что и требовалось доказать.
Задача 2
В прямоугольном треугольнике тангенс угла А равен  . Доказать, что синус угла А равен
. Доказать, что синус угла А равен  .
.
Решение:
Рассмотрим прямоугольный треугольник АВС (∟С = 90˚):
В
 А
А
С
tg ∟A =  , tg A = 60˚, значит, ∟A = 60˚, sin A = 60˚ =
, tg A = 60˚, значит, ∟A = 60˚, sin A = 60˚ =  , что и требовалось доказать.
, что и требовалось доказать.
Такие задачи способствуют осознанному восприятию определения синуса, косинуса и тангенса острого угла прямоугольного треугольника, а также закреплению формул приведения.
Задача 3
Доказать, что в прямоугольном треугольнике  55˚ +
55˚ +  55˚ = 1.
55˚ = 1.
Решение:
 α +
α +  α = 1 - основное тригонометрическое тождество, которое выполняется при любых значениях α, таким образом оно будет выполняться и при α = 55˚, то есть
α = 1 - основное тригонометрическое тождество, которое выполняется при любых значениях α, таким образом оно будет выполняться и при α = 55˚, то есть  55˚ +
55˚ +  55˚ = 1.
55˚ = 1.
Задача 4
Доказать, что в прямоугольном треугольнике sin 35˚ = cos 65˚.
Решение:
Рассмотрим прямоугольный треугольник АВС (∟С = 90˚):
Сначала докажем, что sin A = sin (90˚ - ∟В),
sin A = cos B, так как ∟А + ∟В = 90˚, то ∟А = 90˚ - ∟В,
sin A = sin (90˚ - ∟В) = cos B, 35˚ = cos 65˚, что и требовалось доказать
Такие задачи способствуют закреплению формул приведения и основного тригонометрического тождества, развитию логического и аналитического мышления.
Заключение
В ходе работы над проблемой - решение задач по геометрии с применением тригонометрии в курсе математики 8 класса, были изучены объект и, предмет исследования, которые показали необходимость осознанности работы над такими задачами.
В ходе исследования выяснено, что рациональное решение геометрических задач по тригонометрии является одной из самых актуальных в современной методике. Так как тригонометрия традиционно является одной из важнейших составных частей школьного курса математики, представляет собой его целостный и самостоятельный раздел.
Установлено, что решение задач по геометрии с применением тригонометрии способствует более рациональной работе с задачами.
Решение задач на вычисление способствует развитию аналитического и логического мышления, что необходимо в современной жизни.
Решение задач на построение способствует развитию конструктивного мышления и эстетического вкуса учащихся.
Решение задач на доказательство способствует формированию аналитического, логического и пространственного мышления учащихся.
Установлено, что систематическая работа по формированию навыков решения задач по геометрии с применением тригонометрии способствует развитию общего интеллектуального развития учащихся, их творческих способностей, потенциала школьника, умению разбираться в создавшейся ситуации, делать нужные умозаключения. Основным средством развития творческих способностей ученика является решение задачи, при этом главная цель - не получение результата решения задачи, а само решение задачи, как совокупность логических шагов, приводящих к получению ответа. Очень важно научить ученика использовать оптимальные методы решения задач, среди которых тригонометрический метод является наиболее простейшим.
Цель курсовой работы достигнута: изучены различные методические подходы к решению задач по геометрии с применением тригонометрии в курсе математики 8 класса.
Таким образом, подтвердилась выдвинутая гипотеза, оптимальный подход к решению задач по геометрии с применением тригонометрии будет способствовать развитию аналитического, логического, конструктивного мышления учащихся и формированию их математической зоркости.
|
|
|


