 |
Как складываются и умножаются понятия?
|
|
|
|
Помимо ограничения, обобщения, определения и деления понятий существуют еще две логические операции – сложение и умножение понятий.
Сложение понятий – это логическая операция объединения двух и большего количества понятий, в результате которой образуется новое понятие с объемом, охватывающим собой все элементы объемов исходных понятий. Например, при сложении понятий школьник и спортсмен образуется новое понятие, в объем которого входят как все школьники, так и все спортсмены. Результат сложения понятий, часто называемый логической суммой, на схеме Эйлера изображается штриховкой:

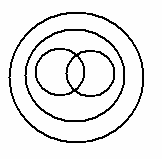
Умножение понятий – это логическая операция объединения двух и большего количества понятий, в результате которой образуется новое понятие с объемом, охватывающим собой только совпадающие элементы объемов исходных понятий. Например, при умножении понятий школьник и спортсмен образуется новое понятие, в объем которого входят только школьники, являющиеся спортсменами и спортсмены, являющиеся школьниками. Результат умножения понятий, часто называемый логическим произведением, на схеме Эйлера изображается штриховкой (так же, как и результат сложения):
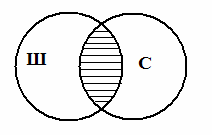

 Мы привели примеры сложения и умножения понятий, которые находятся между собой в отношении пересечения (школьник и спортсмен). В других случаях отношений между понятиями результаты сложения и умножения (логическая сумма и логическое произведение), разумеется, будут иными. Читатель без труда сможет определить их для всех случаев отношений между понятиями с помощью круговых схем. Так, если два понятия находятся в отношении подчинения, например, карась и рыба, то результатом их сложения является родовое понятие рыба (т. е. логической суммой понятий карась и рыба будет множество всех рыб):
Мы привели примеры сложения и умножения понятий, которые находятся между собой в отношении пересечения (школьник и спортсмен). В других случаях отношений между понятиями результаты сложения и умножения (логическая сумма и логическое произведение), разумеется, будут иными. Читатель без труда сможет определить их для всех случаев отношений между понятиями с помощью круговых схем. Так, если два понятия находятся в отношении подчинения, например, карась и рыба, то результатом их сложения является родовое понятие рыба (т. е. логической суммой понятий карась и рыба будет множество всех рыб):
|
|
|

 Р
Р
 | |
 |

 К
К
 |
Результатом умножения понятий карась и рыба, находящихся в отношении родовидового подчинения, будет видовое понятие карась (т.е. логическим произведением понятий карась и рыба является множество всех карасей):
 |
Р
 |

 К
К
 | |||
 |
Так же, если два понятия находятся в отношении соподчинения, например, береза и сосна, то результат их сложения - это два объема данных понятий (т. е. логической суммой понятий береза и сосна будет как множество всех берез, так и множество всех сосен):
 | 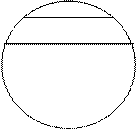 | ||

 Б С
Б С
 | |||||||
 | |||||||
 | |||||||
 | |||||||
Результатом умножения соподчиненных понятий береза и сосна является нулевое понятие (т. е. логическое произведение понятий береза и сосна представляет собой пустое множество - не существует ни одной березы, которая могла бы быть сосной и наоборот):
 | |||
 | |||
Б С
Точно так же устанавливаются результаты сложения и умножения объемов двух понятий, которые находятся в отношениях равнозначности, противоположности и противоречия (см. 1.5.). Так, например, нетрудно догадаться, что если два понятия находятся в отношении равнозначности, то результат их сложения будет полностью совпадать с результатом их умножения (логическая сумма равнозначных понятий равна их логическому произведению). Так же понятно, что результатом умножения противоположных и противоречащих понятий является нулевое понятие и т. п.
Как правило, в естественном языке (т.е. том, на котором мы общаемся) результат сложения понятий выражается союзом или, а умножения – союзом и. В результате сложения понятий школьник и спортсмен образуется новое понятие, в объем которого входит любой человек, если он является или школьником, или спортсменом, а в результате умножения этих понятий в объем нового понятия входит любой человек, если он является и школьником, и спортсменом одновременно.
|
|
|
Относительно употребления союзов или и и в естественном языке в качестве выражения результатов логических операций сложения и умножения понятий удачный пример приводит в своем учебнике по логике известный отечественный автор В. И. Свинцов (Логика. Элементарный курс для гуманитарных специальностей. М.: Скорина, 1998. С. 60 – 61), отрывок из которого приводится ниже. «Что касается союзов «или» и «и», то нужно отметить их многозначность, способную в известных ситуациях создавать достаточно неопределенное представление о характере связи между некоторыми исходными понятиями. Удачна ли, например, следующая формулировка одного из правил пользования городским транспортом: «Безбилетный проезд и бесплатный провоз багажа наказывается штрафом»? Представим себе два подмножества, которые могут быть выделены во множестве пассажиров-нарушителей. В одно из них войдут пассажиры, не взявшие билета, в другое – не оплатившие провоз багажа. Если союз «и» рассматривать как показатель логического умножения, то придется признать, что штраф должен быть наложен только на тех пассажиров, которые совершили сразу два проступка (но не какой-то один из них). Разумеется, житейский смысл ситуации, предусмотренной данным правилом, настолько ясен, что всякие разночтения этой формулировки, вероятно, были бы признаны казуистикой, но все же использование союза «или» здесь следует признать предпочтительным».
Здесь следует отметить неоднозначность разделительного союза или, который может употребляться в нестрогом (неисключающем) значении и в строгом (исключающем). Например, в высказывании: Можно изучать английский язык или немецкий союз или употребляется в нестрогом значении, т.к. можно изучать и тот, и другой язык одновременно, одно другое не исключает. В данном случае разделительный союз или очень близок к соединительному союзу и. С другой стороны, в высказывании: Он родился в 1987 году или в 1989 году союз или употребляется в строгом значении, т.к. если он родился в 1987 году, то – никак не в 1989 году и наоборот, два варианта здесь друг друга исключают. (О различных значениях союза или мы еще будем говорить далее). Если в рассмотренное выше правило пользования городским транспортом поставить союз или вместо союза и, как предлагает В.И. Свинцов, то получится следующее: «Безбилетный проезд или бесплатный провоз багажа наказываются штрафом». В данном случае союз или, являющийся показателем логического сложения, надо воспринимать в его нестрогом, неисключающем значении. Но ведь в указанной фразе этот союз можно истолковать и в строгом, исключающем значении. Тогда получится, что штраф накладывается или только на тех пассажиров, которые не оплатили проезд, или же только на тех, которые бесплатно провозят багаж. Правда, в этом случае не совсем понятно, кто же наказывается штрафом – те или другие. Поразмыслив, можно прийти к выводу, что штрафу подвергаются то те, то другие – на усмотрение контролера и в зависимости от ситуации.
|
|
|
В силу всего сказанного надо отметить, что употребление союза или всякий раз нуждается в комментарии относительно того, в строгом или нестрогом значении он используется. Понятно, что без этого комментария вполне возможны разночтения, которые нередко приводят к различным и существенным недоразумениям.
Вопросы и задания к главе 1
1. Что такое логика? Чем она отличается от многих наук, которые занимаются мышлением? Что такое содержание и форма мышления? Почему логика часто называется формальной логикой? Какие существуют формы мышления? Приведите несколько примеров понятий, суждений и умозаключений. Что такое законы логики? Какую роль они играют в нашем мышлении? Что такое софизмы?
2. Когда и где появилась логика? Кто считается ее создателем? Что такое традиционная логика? Когда появилась символическая, или математическая логика? Какие идеи лежат в ее основе? Чем отличается традиционная логика от символической, и в чем заключается их сходство? Являются ли традиционная логика и символическая логика различными науками? Что называется “исчислениями” в символической логике?
|
|
|
3. Как вы думаете, зачем нужна человеку логика? Какую роль она играет в его жизни? Можно ли, на ваш взгляд, без нее обойтись? Что такое интуитивная логика? Попытайтесь привести примеры, иллюстрирующие тот факт, что даже никогда не изучавшие логику люди все равно интуитивно ей пользуются.
4. Что такое понятие? Как соотносятся понятие и слово? Можно ли утверждать, что понятие и слово – это одно и то же? Что такое содержание и объем понятия? Как они соотносятся? Что представляет собой принцип обратного отношения между содержанием и объемом понятия? Приведите примеры понятий, иллюстрирующие этот принцип.
5. Какими бывают понятия по объему и содержанию? Приведите по 10 примеров для понятий единичных, общих, нулевых, собирательных, несобирательных, конкретных, абстрактных, положительных, отрицательных. Что такое логическая характеристика понятия? Как она составляется? Какие ошибки часто допускаются при составлении логической характеристики понятий?
6. Дайте логическую характеристику следующим понятиям:
1. Луна, 2. растение, 3. столица государства, 4. музыкальный коллектив, 5. знаменитый художник, 6. кентавр, 7. датский физик Нильс Бор, 8. древний философ, 9. Антарктида, 10. Атлантида, 11. сборная России, 12. лист бумаги, 13. молекула воды, 14. преступное сообщество, 15. уровень преступности, 16. невежество, 17. глупость, 18. умный человек, 19. драгоценный камень, 20. пьяная компания, 21. неправда, 22. водород, 23. геометрия, 24. рота солдат, 25. несправедливость, 26. эксплуатация, 27. воздух, 28. философы милетской школы, 29. знаменитое произведение искусства, 30. тишина.
7. Придумайте понятия, соответствующие следующим логическим характеристикам:
общее, несобирательное, конкретное, положительное.
единичное, несобирательное, конкретное, положительное.
единичное, собирательное, конкретное, положительное.
общее, собирательное, конкретное, положительное.
общее, несобирательное, абстрактное, отрицательное.
нулевое, несобирательное, абстрактное, положительное.
нулевое, собирательное, конкретное, положительное.
общее, собирательное, конкретное, отрицательное.
единичное, несобирательное, абстрактное, положительное.
нулевое, несобирательное, конкретное, отрицательное.
8. Что такое определенное понятие? В каком случае можно говорить, что понятие имеет ясное содержание и резкий объем? Что представляют собой неопределенные понятия? Объясните, что такое неясное содержание и нерезкий объем понятия? Каковы основные причины появления и существования неопределенных понятий? Можно ли без них обойтись, вообще исключив их из мышления и языка? Если невозможно, то почему?
|
|
|
9. Представляют ли неопределенные понятия сами по себе, вне зависимости от ситуации, в которой они употребляются, коммуникативные помехи? Почему, на ваш взгляд, употребление неопределенных понятий в повседневном общении не приводит нас к коммуникативным затруднениям? В каких случаях неопределенные понятия могут стать причиной различных затруднений и сыграть негативную роль? Каким образом возможно бороться с ними в этих ситуациях?
10. Почему процедура превращения неопределенного понятия в определенное всегда условна и относительна, в силу чего неопределенное понятие, в конечном итоге, остается неопределенным?
Приведите по десять примеров для определенных и неопределенных понятий.
11. Какие из следующих понятий являются определенными, а какие неопределенными: карась, млекопитающее животное, большая собака, дикая кошка, престижное учебное заведение, московское учебное заведение, планета Нептун, яркая звезда, талантливый человек, богач, бездарный преподаватель, кандидат физико-математических наук, хулиган, известный писатель, высокие горы, учебник по химии, хорошая музыка, скучная лекция, добротная одежда, скромная пища, сборная России по футболу, крупный город, столица государства?
12. Путем прибавления к содержанию следующих понятий каких-либо признаков превратите их из неопределенных в условно определенные: высокий человек, старик, богач, лысый, толстая книга, современная музыка, плохая погода, высокая зарплата, хорошие соседи, двоечник, известный писатель, крупное военное сражение, большой стадион, плохой учитель, несвежие продукты, редкая удача, безрассудный поступок.
13. Что такое сравнимые и несравнимые понятия? Приведите по пять примеров для сравнимых и несравнимых понятий. Какие понятия называются в логике совместимыми, а какие – несовместимыми? Приведите по пять примеров для совместимых и несовместимых понятий.
14. В каких отношениях могут быть совместимые понятия? Что представляют собой отношения равнозначности, пересечения и подчинения между понятиями? Что такое видовые и родовые понятия? В каких отношениях могут быть несовместимые понятия? Что представляют собой отношения соподчинения, противоположности и противоречия между понятиями? Чем отличается противоположность от соподчинения и противоречие от противоположности?
15. Каким образом изображаются отношения между понятиями? В каком отношении находятся понятия, обозначающие часть и целое? Почему между этими понятиями не может быть отношения подчинения?
Почему возможно утверждать, что несравнимые понятия находятся в отношении соподчинения? Приведите пять примеров несравнимых понятий для иллюстрации своего ответа, прокомментировав каждый из них.
16. Почему невозможно точно установить отношения между неопределенными понятиями? Приведите примеры, иллюстрирующие ваш ответ. Приведите по три примера для каждого случая отношений между понятиями: равнозначности, пересечения, подчинения, соподчинения, противоположности и противоречия.
17. В каких отношениях находятся следующие понятия: двоечник и студент, композитор и человек, город и деревня, Антарктида и ледовый материк, небесное тело и звезда, треугольник и сторона треугольника, школа № 5 и учебное заведение, майор и россиянин, знаменитый человек и немецкий писатель, дом и крыша дома, собака и кошка, умный человек и неумный человек, монарх и самодержец, физика и химия, геометрия и тригонометрия, столица и населенный пункт, книга и интересная книга, телевизор и планета солнечной системы, растение и крапива, окружность и круг, Николай II и последний русский царь, олимпийские игры и спортивные состязания?
18. С помощью круговых схем Эйлера изобразите отношения между следующими группами понятий:
а) равносторонний прямоугольник б) Александр Македонский
треугольник монарх
квадрат персонаж древней истории
геометрическая фигура самодержец
в) двигатель г) учащийся
автомобиль двоечник
колесо спортсмен
карданный вал отличник
изделие человека студент
д) естественный спутник е) футболист
спутник планеты спортсмен
Луна всемирно известный футболист
естественный спутник Земли всемирно известный спортсмен
планета Сатурн человек
ж) час з) сестра
секунда тетя (в родственном смысле)
минута мать
сутки бабушка
24 часа дочь
единица времени внучка
19. Подберите понятия, соответствующие следующим схемам:
а) б) 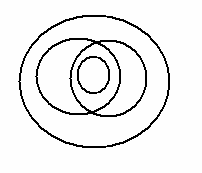
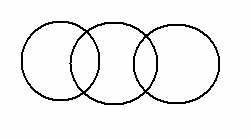
в) г)
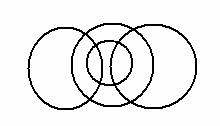
д) е)




20. Что такое ограничение понятия? Почему для уменьшения объема понятия надо прибавлять какие-либо признаки к его содержанию? Что представляет собой логическая операция обобщения понятия? Каким образом ограничения и обобщения понятий складываются в логические цепочки? Каковы пределы цепочек ограничений и обобщений?
21. Какие ошибки часто допускают при ограничении и обобщении понятий? Продемонстрируйте на самостоятельно подобранных примерах, что целое и часть нельзя путать с видом и родом. Всякое ли понятие можно подвергнуть ограничению и обобщению? Какие понятия не поддаются этим логическим операциям?
22. Подберите десять любых понятий и сделайте с каждым из них ограничение и обобщение, т.е. подберите для каждого из них как видовое, так и родовое понятие, иллюстрируя эти операции круговыми схемами Эйлера. Возьмите какое-либо понятие и постройте логическую цепочку его ограничения до предела. Возьмите какое-либо понятие и постройте цепочку его обобщения до предела.
23. Совершите ограничение и обобщение со следующими понятиями: школа, знаменитый писатель, математическое действие, картина, предмет мебели, университет, планета, американский президент, актер, химический элемент, древнегреческий ученый, балет, уровень преступности, музей, историческое событие, яблоня, всемирно известный спортсмен, материк, книга, хищник, высотное здание, молодой человек, музыкальный коллектив, сборная России, ураган, электричество, стихотворение.
24. Какие из приведенных ниже понятий невозможно подвергнуть ограничению или обобщению: тетрадь, МГУ, галактика, русский писатель XIX века, первый космонавт земли, Вселенная, химический элемент, Россия, древнее государство, Солнце, современный автомобиль, млекопитающее животное, небоскреб, атомная электростанция, столица Франции, нечто существующее, планета Юпитер, Третьяковская галерея, московский кинотеатр, толстая книга, бытие?
25. Что представляет собой логическая операция определения понятия? Чем отличаются явные определения от неявных? Придумайте по три примера явных и неявных определений. Что такое реальные и номинальные определения? Как вы думаете, почему возможно утверждать, что любое реальное определение можно свести к номинальному и наоборот?
26. Что представляет собой классический способ определения понятия? Дайте определения каким-нибудь трем понятиям, пользуясь классическим способом определения. Каковы основные правила определения понятия? Какие ошибки возникают при их нарушении? Приведите, подобрав самостоятельно, по три примера для каждой ошибки в определении понятия.
27. Допущены ли ошибки в определениях, приведенных ниже? Если допущены, то какие?
а) Фильтрование – это процесс разделения какого-либо вещества с помощью специального приспособления – фильтра.
б) Кость – это орган, обладающий сложным строением.
в) Бескорыстие – это отсутствие личной заинтересованности при оказании какой-либо помощи.
г) Гравитация – это явление, которое выражается во взаимодействии двух физических тел.
д) Барометр – это метеорологический измерительный прибор.
е) Математика – это гимнастика ума.
ж) Сверхпроводник – это вещество, обнаруживающее явление сверхпроводимости.
з) Логика – это наука о формах и законах правильного мышления.
и) Извлечение квадратного корня – это математическое действие, которое не является ни умножением, ни делением, ни возведением в степень.
28. Что представляет собой логическая операция деления понятия? Чем она отличается от операции определения? Какова структура деления? Что такое основание деления? Какое деление называется дихотомическим? Попробуйте отметить достоинства и недостатки дихотомического деления. Какую роль в научном и повседневном мышлении играет логическая операция деления понятия?
29. Каковы основные логические правила деления понятия? Какие ошибки возникают при их нарушении? Придумайте по три примера для каждой ошибки в делении понятия. Почему дихотомическое деление понятия всегда является безошибочным? Каким образом оно исключает все возможные в делении ошибки?
30. Допущены ли ошибки в приведенных ниже примерах деления? Если допущены, то какие?
а) Воды земного шара бывают пресными и солеными.
б) Учащиеся бывают успевающими, отстающими и отличниками.
в) Речь бывает устной, письменной, путанной и заумной.
г) Спортивные состязания бывают мировыми, международными, олимпийскими и другими.
д) Треугольники бывают тупоугольными и прямоугольными.
е) Жиры бывают растительными, животными и твердыми.
ж) Люди бывают высокими и невысокими.
з) Оружие бывает холодным, огнестрельным и старинным.
и) Высшие учебные заведения делятся на университеты, институты, академии и высшие училища.
31. Что представляют собой логические операции сложения и умножения понятий? Что такое логическая сумма и логическое произведение? Возьмите три пары каких-нибудь понятий и сделайте с ними логические операции сложения и умножения, иллюстрируя их результаты с помощью круговых схем Эйлера.
32. Каковы результаты сложения и умножения понятий во всех случаях отношений между ними? Могут ли эти результаты полностью совпадать? Может ли логическая сумма или логическое произведение быть нулевым понятием?
33. Какие союзы естественного языка являются, как правило, выражением результатов сложения и умножения понятий? Проиллюстрируйте свой ответ самостоятельно подобранными примерами. В чем заключается неоднозначность употребления союза или как показателя логического сложения понятий?
34. Произведите сложение и умножение следующих понятий, изобразив результаты этих операций с помощью круговых схем Эйлера: майор и военнослужащий, атом и молекула, квадрат и ромб с прямым углом, известный актер и россиянин, млекопитающее животное и лошадь.
Глава 2. Суждение
2.1. Что такое суждение?
Суждение - это вторая после понятия форма мышления. Суждением называется форма мышления, в которой что-либо утверждается или отрицается. Примеры суждений: Все сосны являются деревьями; Некоторые люди – это спортсмены; Ни один кит – не рыба; Некоторые животные не являются хищниками и т.п. Суждение также называется высказыванием.
Рассмотрим несколько важных свойств суждения, которые также являются его отличиями от понятия.
1. Любое суждение состоит из понятий, связанных между собой. Например, если связать между собой понятия карась и рыба, то может получиться суждение: Все караси являются рыбами или Некоторые рыбы являются карасями.
2. Любое суждение выражается в форме предложения (вспомним, понятие выражается в слове или словосочетании). Однако не всякое предложение может выражать суждение. Как известно, предложения бывают повествовательными, вопросительными и восклицательными. Суждение – это форма мышления, в которой что-либо утверждается или отрицается. В вопросительных и восклицательных предложениях ничего не утверждается и не отрицается, поэтому они не могут выражать собой суждение. Повествовательное предложение, наоборот, всегда представляет какое-то утверждение или отрицание, в силу чего суждение выражается в форме повествовательного предложения. Тем не менее, есть такие вопросительные и восклицательные предложения, которые только по форме являются вопросами и восклицаниями, а по смыслу что-то утверждают или отрицают. Они называются риторическими. Например, известное высказывание: И какой же русский не любит быстрой езды? представляет собой риторическое вопросительное предложение (или риторический вопрос), т.к. в нем в форме вопроса утверждается, что всякий русский любит быструю езду. Такой вопрос, конечно же, выражает собой суждение. То же самое можно сказать о риторических восклицаниях. Например, в высказывании: Попробуй найти черную кошку в темной комнате, если ее там нет! в форме восклицательного предложения утверждается мысль о невозможности предложенного действия, в силу чего данное восклицание выражает собой суждение. Понятно, что не риторический, а настоящий вопрос, например: Как тебя зовут? не выражает собой суждение, точно так же, как не выражает его настоящее, а не риторическое восклицание, например: Прощай, свободная стихия! Приведем еще несколько примеров.
а) Неужели ты не знал, что Земля вращается вокруг Солнца? (риторический вопрос - является суждением).
б) Прощай, немытая Россия! (восклицание - суждением не является).
в) Кто написал философский трактат «Критика чистого разума»? (вопрос - суждением не является).
г) Логика появилась примерно в V в. до н.э. в Древней Греции (повествование - является суждением).
д) первый президент Америки (понятие - суждением не является).
е) Разворачивайтесь в марше! (восклицание - суждением не является).
3. Любое суждение является истинным или ложным. Если суждение соответствует действительности или реальности, оно истинное, а если не соответствует, - ложное. Например, суждение: Все розы – это цветы является истинным, а суждение: Все мухи – это птицы – ложным. Надо отметить, что понятия, в отличие от суждений, не могут быть истинными или ложными. Невозможно, например, утверждать, что понятие школа – истинное, а понятие институт – ложное, понятие звезда – истинное, а понятие планета – ложное и т.п. Но разве понятия Змей Горыныч или Кощей Бессмертный, или вечный двигатель не ложные? Нет, не ложные, эти понятия являются нулевыми или пустыми, но не истинными и не ложными. Вспомним, понятие – это форма мышления, которая обозначает собой какой-либо объект, – и именно поэтому не может быть истинным или ложным. Истинность или ложность – это всегда характеристика какого-то высказывания, утверждения или отрицания, в силу чего она применима только к суждениям, но не к понятиям. Поскольку любое суждение принимает одно из двух значений – истины или лжи, – то аристотелевская формальная логика также часто называется двузначной логикой.
4. Суждения бывают простыми и сложными. Сложные суждения состоят из простых, соединенных каким-либо союзом. О простых и сложных суждениях речь пойдет далее.
Структура суждения
Суждение – это более сложная форма мышления по сравнению с понятием. Неудивительно поэтому, что суждение имеет определенную структуру, в которой можно выделить четыре части.
1. Субъект (обычно обозначается латинской буквой S) – это то, о чем идет речь в суждении. Например, в суждении: Все учебники являются книгами речь идет об учебниках, поэтому субъектом данного суждения выступает понятие учебники.
2. Предикат (обычно обозначается латинской буквой Р) – это то, что говорится о субъекте. Например, в том же суждении: Все учебники являются книгами о субъекте (т.е. об учебниках) говорится, что они – книги, поэтому предикатом данного суждения выступает понятие книги.
3. Связка – это то, что соединяет субъект и предикат. В роли связки могут быть слова есть, является, это и т.п.
4. Квантор – это указатель на объем субъекта. В роли квантора могут быть слова все, некоторые, ни один и т.п. Рассмотрим суждение: Некоторые люди являются спортсменами. В нем субъектом выступает понятие люди, предикатом – понятие спортсмены, роль связки играет слово являются, а слово некоторые представляет собой квантор. Если даже в каком-то суждении (выраженном в форме предложения) отсутствует связка или квантор, то они все равно подразумеваются. Например, в суждении: Тигры – это хищники квантор отсутствует, но он подразумевается – это слово все. С помощью условных обозначений субъекта и предиката у любого суждения можно отбросить его содержание и оставить только его логическую форму. Например, если у суждения: Все прямоугольники – это геометрические фигуры отбросить содержание и оставить форму, то получится: Все S есть Р. Точно так же логическая форма суждения: Некоторые животные не являются млекопитающими – Некоторые S не есть Р.
Субъект и предикат любого суждения всегда представляют собой какие-либо понятия, которые, как мы уже знаем, могут находиться в различных отношениях между собой. Между субъектом и предикатом суждения могут быть следующие отношения.
1. Равнозначность. В суждении: Все квадраты – это равносторонние прямоугольники субъект (квадраты) и предикат (равносторонние прямоугольники) находятся в отношении равнозначности, потому что представляют собой равнозначные понятия (квадрат – это обязательно равносторонний прямоугольник, а равносторонний прямоугольник – это обязательно квадрат).
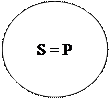 |
2. Пересечение. В суждении: Некоторые писатели – это американцы субъект (писатели) и предикат (американцы) находятся в отношении пересечения, т.к. являются пересекающимися понятиями (писатель может быть американцем и может им не быть, и американец может быть писателем, но также может им не быть).
 |

 S P
S P
 | |||
 |
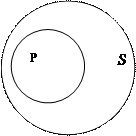
3. Подчинение. В суждении: Все тигры – это хищники субъект (тигры) и предикат (хищники) находятся в отношении подчинения, потому что представляют собой видовое и родовое понятия (тигр – это обязательно хищник, но хищник – не обязательно тигр). Также в суждении: Некоторые хищники являются тиграми субъект (хищники) и предикат (тигры) находятся в отношении подчинения, будучи родовым и видовым понятиями. Понятно, почему в случае подчинения между субъектом и предикатом суждения возможны два варианта отношений: объем субъекта полностью включается в объем предиката или наоборот.
 |  |
4. Несовместимость. В суждении: Все планеты не являются звездами субъект (планеты) и предикат (звезды) находятся в отношении несовместимости, т.к. являются несовместимыми (соподчиненными) понятиями (ни одна планета не может быть звездой, и ни одна звезда не может быть планетой).
 |  |
Чтобы установить, в каком отношении находятся субъект и предикат того или иного суждения, надо сначала установить какое понятие данного суждения является субъектом, а какое – предикатом, после чего определить вид отношения между ними. Например, надо определить отношение между субъектом и предикатом в суждении: Некоторые военнослужащие являются россиянами. Сначала находим субъект суждения, – это понятие военнослужащие; затем устанавливаем его предикат, – это понятие россияне. Понятия военнослужащие и россияне находятся в отношении пересечения (военнослужащий может быть россиянином и может им не быть, и россиянин может как быть, так и не быть военнослужащим), следовательно, в указанном суждении субъект и предикат пересекаются. Точно так же в суждении: Все планеты – это небесные тела субъект и предикат находятся в отношении подчинения, а в суждении: Ни один кит не является рыбой субъект и предикат несовместимы. Приведем еще несколько примеров, иллюстрирующих различные отношения между субъектом и предикатом в суждениях.
а) Все бактерии являются живыми организмами (подчинение).
б) Некоторые русские писатели – это всемирно известные люди (пересечение).
в) Учебники не могут быть развлекательными книгами (несовместимость).
г) Антарктида представляет собой ледовый материк (равнозначность).
Виды суждений
Обычно суждения подразделяют на три вида.
1. Атрибутивные суждения – это суждения, в которых предикат представляет собой какой-либо существенный, неотъемлемый признак или атрибут (лат. аttributum) субъекта. Например, суждение: Все воробьи – это птицы – атрибутивное, потому что его предикат является неотъемлемым признаком субъекта: быть птицей – это главный, неотъемлемый признак воробья, его атрибут, без которого он не будет самим собой, т.е. воробьем (если некий объект не птица, то он обязательно и не воробей). Надо отметить, что в атрибутивном суждении не обязательно предикат является атрибутом субъекта, может быть и наоборот – субъект представляет собой атрибут предиката. Например, в суждении: Некоторые птицы – это воробьи (как видим, по сравнению с вышеприведенным примером, субъект и предикат поменялись местами) субъект является неотъемлемым признаком или атрибутом предиката. Однако эти суждения всегда можно формально изменить таким образом (как мы только что увидели), что предикат станет атрибутом субъекта. Поэтому обычно атрибутивными называются те суждения, в которых предикат является атрибутом субъекта.
2. Экзистенциальные суждения – это суждения, в которых предикат указывает на существование (лат. еxistentia – существование) или несуществование субъекта. Например, суждение: Вечных двигателей не бывает является экзистенциальным, т.к. его предикат (выраженный здесь не совсем обычно – глаголом с частицей «не») свидетельствует о несуществовании субъекта (вернее – о несуществовании предмета, который обозначе
|
|
|


