 |
Поток в транспортной сети.
|
|
|
|
Содержание
Введение………………………………………………………………3стр
Теоретическая часть………………………………………..…………3стр
Теорема Форда-Фалкерсона………………………………………….4стр
Алгоритм решения……………………………………………...…….5стр
Поток в транспортной сети…………………………………………..7стр
Орграф приращений………………………………………………..…7стр
Алгоритм построения максимального потока
В транспортной сети…………………………………….……………7стр
Практическая часть………………………………………………………………....…9стр
Этап 1…………………………………………………………………10стр
Этап 2………………………………………………………………... 11стр
Этап 3………………………………………………………………....12стр
Этап 4……………………………………………………………...….13стр
Этап 5…………………………………………………………………14стр
Этап 6…………………………………………………………………15стр
Заключение…………………………………………………………..16стр
Список используемой литературы……………………………..…..17стр
Введение.
В задаче, которую я рассматриваю, да и вообще в задачах на данную тему фундаментальную роль играет изучение поперечных сечений сети (то есть множеств дуг, которые соединяют вершины двух не пересекающихся множеств вершин) и нахождение ограниченного поперечного сечения, которое является самым узким местом. Эти узкие места определяют пропускную способность системы в целом.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ:
Транспортной сетью называется конечный Связный орграф G(V, E) без петель, каждой дуге которого поставлено в соответствие некоторое неотрицательное число c(
), называемое пропускной способностью дуги, и существует:
1) ровно одна вершина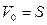 
, в которую не заходит ни одна дуга, называемая источником или началом сети;
|
|
|
2) ровно одна вершина 
, из которой не выходит ни одной дуги; эта вершина называется стоком или концом сети.
Потоком сети называется неотрицательная функция f(1) такая, что f(e) меньше или равно c(e). (Поток не может превышать пропускную способность дуги.)
Дуга 
называется насыщенной потоком f, если 
(Поток называется полным, если содержит насыщенную дугу f(e)=c(e).)
Разрезом L сети G(V,E) называется множество насыщенных дуг, отделяющих источник s от стока t.
Теорема Форда-Фалкерсона.
Пусть D – транспортная сеть, 
- допустимый поток в этой сети, 
- множество вершин 
таких, что длина минимального пути из 
в 
в орграфе приращений 
равна нулю. Тогда, если 
, то - максимальный поток, величина которого равна 
.
Пусть . Тогда выполняется равенство
(1)
Если 
, так как в противном случае, используя 
имеем 
, а следовательно, в силу 
существует путь нулевой длины из 
в , что противоречит условию 
. Но тогда из (1) получаем
Следствие 1. Используя теорему Форда-Фалкерсона получаем, что величина максимального потока в транспортной сети равна пропускной способности минимального разреза.
Следствие 2. Пусть - допустимый поток в транспортной сети D. Тогда, если длина минимального пути из v1 в vn в орграфе приращений равна бесконечности, то - максимальный поток.
Алгоритм решения.
Сначала будем строить полный поток, затем проверим, можно ли его увеличить. Если нет, то этот поток является максимальным. Если же его можно увеличить, то будем строить другой полный поток и т.д. Решать задачу будем с помощью метода расстановки пометок.
Две основные процедуры (операции алгоритма):
· операция расстановки пометок;
· операция изменения потока.
Рассмотрим первую процедуру. Для каждой вершины данной сети нужно приписать пометку, которая имеет следующий вид: 
или 
где , а – натуральное число или бесконечность. Вообще возможны три состояния вершины:
|
|
|
1) не помечена;
2) помечена, но не просмотрена;
3) помечена и просмотрена.
Расставлять пометки начнем с источника S. Он получит пометку 
Источник помечен, но не просмотрен. Остальные вершины не помечены. Чтобы источник S был помечен и просмотрен, надо поместить все вершины, смежные с S.
Вершина 
получит пометку 
, где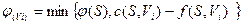 
.
Теперь все вершины смежные с S, помечены, но не просмотрены. А вершина S помечена и просмотрена. Начнём просматривать ту из вершин , которая имеет наименьший индекс. Для этого нужно расставить пометки вершинам, смежным с . Если для вершины 
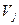выполняется следующее условие 
, то она получит метку 
, где 
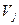. Если же для вершины выполняется условие 
, то 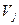получает метку 
, где 
. Далее просматриваем следующую вершину, и так до тех пор, пока не пометим сток t или же пока нельзя будет больше пометить ни одной вершины, сток при этом останется не помеченным. Если сток окажется не помеченным, то процесс нахождения максимального потока в сети можно считать законченным, а если сток помечен, то нужно переходить к
процедуре 2.
Рассмотрим процедуру изменения потока. Если вершина 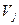имеет пометку , то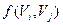 
заменяем на 
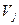, если же вершина имеет пометку , то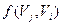 
заменяем на 
Переходим к следующей вершине и так до тех пор, пока не достигнем источника S. Здесь изменение потока прекращается. Далее переходим к процедуре 1 и так до тех пор, пока величину потока уже нельзя изменить.
Рассмотрим конкретную задачу о нахождении максимального потока в сети.
Дана сеть G(V,E) (рис. 11) с источником S и стоком t. Пропускные способности дуг указаны. Найти максимальный поток из S в t.
Поток в транспортной сети.
Функция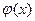 
, определенная на множестве X дуг транспортной сети D и принимающая целочисленные значения, называется допустимым потоком (или просто потоком) в транспортной сети D, если:
•для любой дуги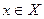 
величина 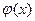, называемая потоком по дуге 
, удовлетворяет условию 
;
•для любой промежуточной вершины v выполняется равенство
т.е. сумма потоков по дугам, заходящим в v, равна сумме потоков по дугам, исходящим из v.
Орграф приращений.
Введем для заданной транспортной сети D и допустимого потока в этой сети орграф приращений , имеющий те же вершины, что и сеть D. Каждой дуге 
транспортной сети D в орграфе приращений соответствует две дуги: и 
- дуга, противоположная по направлению дуге . Припишем дугам 
орграфа приращений длину 
:
|
|
|
т.е. орграф является нагруженным. При этом очевидно, что длина любого пути из 
в 
в орграфе равна либо 0, либо бесконечности.
|
|
|
