 |
Алгоритм построения максимального потока в транспортной сети.
|
|
|
|
Важным следствием теоремы Форда-Фалкерсона является Алгоритм построения максимального потока в транспортной сети.
Алгоритм:
Шаг 1. Полагаем i=0. Пусть 
- любой допустимый поток в транспортной сети D (например, полный, можно начинать с нулевого потока: 
).
Шаг 2. По сети D и потоку 
строим орграф приращений 
.
Шаг 3. Находим простую цепь 
, являющуюся минимальным путем из 
в 
в нагруженном орграфе . Если длина этой цепи равна бесконечности, то поток максимален, и работа алгоритма закончена. В противном случае увеличиваем поток ввдоль цепи на максимально допустимую величину 
, такую, что при этом сохраняется условие 1 допустимого потока (для любой дуги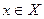 
величина 
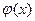, называемая потоком по дуге х, удовлетворяет условию 
). В силу 
, используя 
и 
, получаем, что указанная величина 
существует. В результате меняется поток в транспортной сети D, т.е. от потока мы перешли к потоку 
, и при этом 
. Присваеваем 
и переходим к шагу 2.
ПРАКТИЧЕСКАЯ ЧАСТЬ:
Задача о максимальном потоке.
Для заданной транспортной сети определить величину максимального потока грузов, которые можно доставить в течение заданного времени из города S в город t. Пропускные способности всех участков дорог считаются известными.
Этап 1.
Начнём с процедуры расстановки пометок. Пометка источника S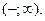 
Далее рассмотрим те вершины, которые соединены с источником дугой. Это V1, V2,. Пропустим по всей сети первоначальный нулевой поток 
Припишем около каждой дуги после значения пропускной способности значение первоначального потока.
Просмотрим вершину S, для этого пометим вершиныV1, V3
Просмотрим вершину V1,пометим вершины v2
Просмотрим вершину V2,пометим вершины V4 и V7
|
|
|
Просмотрим вершину V4,пометим вершины V5 и V6
Просмотрим вершину V6,пометим вершину T
Ставим изменение потока:
f1=4
S=>V1=>V2=>V4=>V6=>T
Дуга V4V6 становится насыщенной
Этап 2.
Просмотрим вершину S, для этого пометим вершиныV1, V3
Просмотрим вершину V1,пометим вершины v2
Просмотрим вершину V2,пометим вершины V4 и V7
Просмотрим вершину V4,пометим вершины V5
Просмотрим вершину V5 пометим вершину V6
Просмотрим вершину V6,пометим вершину T
Ставим изменение потока:
F2=6
S=>V1=>V2=>V4=>V5=>V6=>T
Дуга V1V2 становится насыщенной
|
|
Этап 3.
Просмотрим вершину S, для этого пометим вершиныV1, V3
Просмотрим вершину V3 пометим вершину V4
Просмотрим вершину V4,пометим вершины V5,V2
Просмотрим вершину V5 пометим вершину V6
Просмотрим вершину V6,пометим вершину T
Ставим изменение потока:
F3=1
S=>V3=> V4=>V5=>V6=>T
Дуга V5V6 становится насыщенной
Этап 4.
Просмотрим вершину S, для этого пометим вершиныV1, V3
Просмотрим вершину V3 пометим вершину V4
Просмотрим вершину V4,пометим вершины V2
Просмотрим вершину V2 пометим вершину V7
Просмотрим вершину V7,пометим вершину T
Ставим изменение потока:
F4=10
S=>V3=> V4=>V2=>V7=>T
Этап 5.
Просмотрим вершину S, для этого пометим вершиныV1, V3
Просмотрим вершину V3 пометим вершину V4
Просмотрим вершину V4,пометим вершины V5
Просмотрим вершину V5 пометим вершину V7
Просмотрим вершину V7,пометим вершину T
Ставим изменение потока:
F5=8
S=>V3=> V4=>V5=>V7=>T
Дуга V5V7 становится насыщенной
Этап 6
Просмотрим вершину S, для этого пометим вершиныV1, V3
Просмотрим вершину V3 пометим вершину V4
Просмотрим вершину V4,пометим вершины V5
F=0+6+1+10+8+4=29
L:8+7+4+10=29
(V1V2),(V4V6),(V5V6),(V5V7)
Заключение.
Бурное развитие дискретной математики обусловлено прогрессом компьютерной техники, необходимостью создания средств обработки и передачи информации, а также представления различных моделей на компьютерах, являющихся по своей природе конечными структурами.
|
|
|
Транспортной сетью называется конечный Связный орграф G(V, E) без петель, каждой дуге которого поставлено в соответствие некоторое неотрицательное число c(
), называемое пропускной способностью дуги, и существует:
1) ровно одна вершина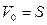 
, в которую не заходит ни одна дуга, называемая источником или началом сети;
2) ровно одна вершина 
, из которой не выходит ни одной дуги; эта вершина называется стоком или концом сети.
Список используемой литературы
1. А.М. Аллавердиев, И.В. Платонова «Прикладная математика. Элементы теории графов» М.2000
2. Лекции по прикладной математике И.В. Платоновой
3. В.Н. Нефедов, В.А. Осипова «Курс дискретной математики» М. 1992
4. С.В. Судоплатов, Е.В. Овчинникова «Элементы дискретной математики» М. 2002
|
|
|
