Перевод чисел из десятичной системы счисления в систему счисления с другим основанием

II ДВОИЧНАЯ АРИФМЕТИКА

Арифметические операции с числами в двоичной системе счисления

 

Пример. Найти сумму двоичных дробных чисел и .

Решение.

[1]

[1]

[1]

[1]

[1]

[1]

[1]

[1]

[1]

[1]

[1]

[1]

[1]

[1]

+

1,

02

1,

12

1,

12

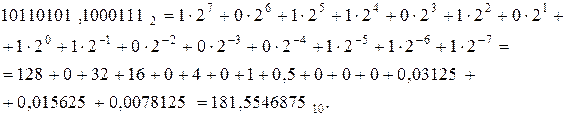
181,5546875₁₀+93,96484375₁₀=275,51953125₁₀.

Пример. Найти разность двоичных дробных чисел и .

Решение.

						[1]	[1]				[1]	[1]					заёмы из старших разрядов
-								0,							12		уменьшаемое
							1,								12	вычитаемое
								1,								12	разность

 

 

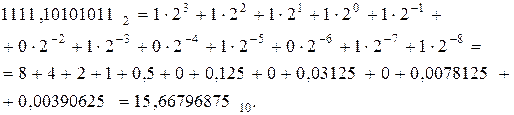
88,7734375₁₀-15,6679687₁₀=73,10546875₁₀.

При умножении двух двоичных дробных чисел необходимо придерживаться следующих трёх правил:

- числа перемножаются без учета запятых;

-

- в полученном произведении запятая ставится так, чтобы отделить справа столько же знаков, сколько отделено в обоих множителях вместе взятых.

Пример.

Найти произведение двоичных дробных чисел и .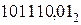

Решение. Операция нахождения произведения указанных дробных двоичных чисел требует выполнения сложений неполных произведений, что в свою очередь требует проведения большого количества переносов в старшие разряды. Для повышения наглядности пронумеруем разряды и приведем результаты поразрядных сложений.

 

0,

12

множимое

0,

12

множитель

[1]

[1]

[1]

[1]

[1]

[1]

[1]

[1]

переносы в старшие разряды

+

неполные произведения

+

+

+

1,

12

результат операции произведения

 

Поразрядное сложение неполных произведений (строки 4 по 8) подробно описано ниже:

0 разряд = 1;
1 разряд = 0;
2 разряд = 1;
3 разряд = 0+1=1;
4 разряд = 1+0+1=10 (0 пишем в 4 разряде, 1 переносим в 5 разряд [1]);
5 разряд=[+1]+0+1+0+1=11 (1 пишем в 5 разряде, 1 переносим в 6 разряд [1]);
6 разряд = [+1]+0+0+1+0=10;
7 разряд = [+1]+1+1+0+1+1=101 (1 пишем в 7 разряде, 0 переносим в 8 разряд, 1 переносим в 9 разряд [1]);
8 разряд =0+1+0+0=1;
9 разряд = [1]+0+0+1+1=11;
10 разряд = [1]+1+0+0+0=10;
11 разряд = [1]+1+0+1=11;
12 разряд = [1]+1+0=10;
13 разряд = [1]+0=1;
14 разряд = 1.

 

 

 

 

Пример.

Найти частное двоичных дробных чисел и с точностью до пяти знаков после запятой.

		[1]	[1]
-										0,		12						12
															1,					02
							[1]
			-
							[1]
				-
					-
								[1]	[1]	[1]	[1]	[1]
						-

 

 

 

 

 

Общая формула представления числа в развернутой форме записи в позиционной системе счисления с основанием , имеет вид:

(1)

где 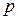- основание системы счисления числа , состоящего из разрядов ( разрядов целой части и разрядов дробной части); - цифра целой части числа , отстоящая на позиций от запятой влево, ; - цифра дробной части числа , отстоящая на позиций от запятой вправо, ; − вес цифры числа .

Как видно из (1), развернутая форма записи числа равна сумме произведений каждой цифры числа на соответствующий ее вес цифры.

Из одной системы счисления в другую могут быть переведены, как целые, так и дробные числа. На первый взгляд, такой перевод кажется ординарным, однако для компьютерной техники это далеко непростая задача, так как связана с архитектурой компьютера. Трудность составляет размещение периодических и непериодических дробей, так как ресурсы компьютера не бесконечны. Решением проблемы является округление дробей и задание класса точности чисел, участвующих в вычислениях и появляющихся в их результате.

 

III ПЕРЕВОД ЧИСЕЛ ИЗ ОДНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ДРУГУЮ

Перевод чисел в десятичную систему счисления из других систем счисления

Пример.

Перевести в десятичную систему счисления c точностью до пяти знаков после запятой следующие числа: ; ; ,

Решение.

 

 

Перевод чисел из десятичной системы счисления в систему счисления с другим основанием

Перевод числа 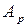из десятичной системы счисления в систему счисления с любым другим основанием производится по следующему алгоритму:

Шаг 1. Целую часть исходного числа 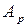делят нацело на основание системы, в которую осуществляется перевод, запоминая остаток. Если неполное частное, полученное от очередного деления, не равно нулю, то его делят нацело. Если равно нулю, то остатки от делений записываются в обратном порядке.

Шаг 2. Дробную часть исходного числа 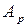умножают на основание системы счисления, в которую осуществляется перевод, запоминая при этом целые части полученных произведений, причем целые части произведений отбрасываются, то есть они в дальнейшем умножении участия не принимают. Умножение производится до тех пор, пока либо не будет получен ноль в дробной части произведения, либо не будет достигнута необходимая точность вычисления. После окончания умножений полученные целые части произведений записываются в прямом порядке.

Шаг 3. Результирующие числа, полученные на Шаге 1 и Шаге 2, складываются.

Пример.

Перевести числа и в следующие системы счисления с точностью до пяти знаков после запятой:

a) двоичную;

б) восьмеричную;

в) шестнадцатеричную.

Решение.

a) Перевод чисел в двоичную систему счисления.

Переведем целую часть числа в двоичную систему счисления:

.

Переведем дробную часть числа в двоичную систему счисления:

Так как в дробной части произведения получен ноль, то перевод дробной части завершен, а для получения заданной количества знаков после запятой оставшиеся две позиции дробной части необходимо заполнить незначащими нулями.

Получив целую и дробную части числа в двоичном виде , получим результирующее число:

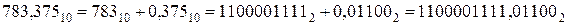, значит .

Переведем целую часть числа в двоичную систему счисления:

.

Переведем дробную часть числа в двоичную систему счисления:

Необходимое число знаков после запятой получено, поэтому вычисления останавливаются.

.

б) Перевод в восьмеричную систему счисления.

Переведем целую часть числа 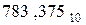в восьмеричную систему счисления:

.

Переведем дробную часть числа 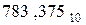в восьмеричную систему счисления:

.

Переведем целую часть числа в восьмеричную систему счисления:

.

Переведем дробную часть числа в восьмеричную систему счисления:

.

в) Перевод в шестнадцатеричную систему счисления.

Переведем целую часть числа в шестнадцатеричную систему счисления:

.

Переведем дробную часть числа в шестнадцатеричную систему счисления:

.

Переведем целую часть числа в шестнадцатеричную систему счисления:

.

Переведем дробную часть числа в шестнадцатеричную систему счисления:

.

 

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: