 |
Перевод чисел в двоичную, восьмеричную и шестнадцатеричную системы счисления
|
|
|
|
Для перевода восьмеричного числа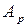 
в двоичную систему счисления 
необходимо каждую цифру исходного восьмеричного числа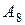 
заменить эквивалентной ей двоичной триадой.
Пример. Перевести восьмеричное число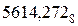 
в двоичную систему счисления.
Решение.
|
Для перевода шестнадцатеричного числа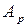 
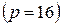в двоичную систему счисления необходимо каждую цифру исходного шестнадцатеричного числа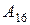 
заменить эквивалентной ей двоичной тетрадой.
Пример. Перевести шестнадцатеричное число 
в двоичную систему счисления.
Решение.
|
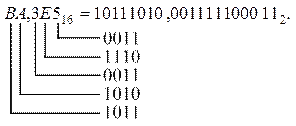
Для перевода двоичного числа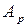 
в восьмеричную систему счисления 
исходное двоичное число 
необходимо разбить на триады, а затем каждую триаду заменить соответствующей восьмеричной цифрой.
При выделении триад для целой части числа триады берутся, начиная с младшего разряда, а для дробной, начиная со старшего разряда. В случае необходимости старшая триада целой части дополняются незначащими нулями слева, а младшая триада дробной части − справа.
Пример. Перевести двоичное число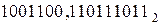 
в восьмеричную систему счисления.
Решение.
|
Для перевода двоичного числа 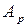в шестнадцатеричную систему счисления 
исходное двоичное число необходимо разбить на тетрады, а затем каждую тетраду заменить соответствующей шестнадцатеричной цифрой.
При выделении тетрад для целой части числа тетрады берутся аналогично тому, как формируются триады при переводе чисел из восьмеричной системы счисления в двоичную.
Пример.Перевести двоичное число 
в шестнадцатеричную систему счисления.
Решение.
|
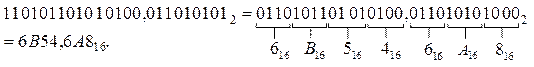
Для перевода восьмеричного числа 
в шестнадцатеричную систему счисления и обратно, необходим промежуточный перевод числа в двоичную систему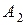 
.
|
|
|
Пример. Перевести восьмеричное число 
в шестнадцатеричную систему счисления.
Решение.
|
Пример. Перевести шестнадцатеричное число 
в восьмеричную систему счисления.
Решение.
Вещественное число 
может быть представлено в двух следующих форматах:
- с фиксированной точкой;
- c плавающей точкой.
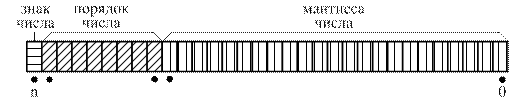
Формат представления действительного числа с плавающей точкой проиллюстрирован на рисунке 1.
|
| Рисунок 1 – Представление числа в формате с плавающей запятой |
В компьютерной арифметике используются следующие коды для представления двоичных чисел с фиксированной точкой:
- прямой код;
- обратный код;
- дополнительный код.
Прямой код двоичного числа совпадает с записью самого числа. Чаще всего прямой код используется для записи беззнаковых (неотрицательных) чисел. Если же прямой код применяется для представления знаковых чисел (то есть как положительных, так и отрицательных чисел), то в дополнение к цифровым разрядам числа вводится еще и старший знаковый разряд (старший бит) (рис. *). Если значение знакового разряда равно 0 - то число положительное, если 1 - отрицательное. В цифровых разрядах записывается двоичное представление модуля числа.
| Рисунок 2 - Представление в компьютерной арифметике знакового числа |
Пример.
| десятичное[КОА1] число | код представления двоичного числа | ||
| прямой | |||
| -9 | |||
| |||
|
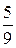
естественной форме (“с фиксированной точкой”) и нормализованной форме (“с плавающей точкой”).
В естественной форме число состоит из целой и дробной частей, между которыми помещается разделитель (запятая или точка). Например, 710,78. Такая запись неудобна для слишком больших или слишком малых чисел. Кроме того, использование такой формы в компьютере вызвало бы снижение точности вычислений и привело бы к снижению точности вычислений из-за необходимости приведения в соответствие разрядов обрабатываемых чисел и связанных с этим округлений или могло бы породить ситуацию, называемую переполнением, когда старший разряд числа не умещается в отведенной разрядной сетке.
|
|
|
Вещественные числа в компьютере представляются в нормализованной форме. Главным достоинством такого представления является автоматическое масштабирование числа при каждом этапе обработке, что, с одной стороны, обеспечивает максимально возможную точность вычислений, а с другой – в большинстве случаев избавляет от необходимости принимать меры по предотвращению переполнения. Формат числа с плавающей точкой имеет вид:
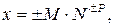
| (1) |
где 
- мантисса нормализованного числа - число, представляющее значение вещественного числа без учета порядка, значение мантиссы лежит в интервале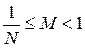 
(то есть первая значащая цифра мантиссы всегда ненулевая);
- основание системы счисления;
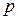- порядок (экспонента числа) - целое число, выражающее степень основания числа, на которое умножается мантисса; 
- характеристика числа.
Представление числа в нормализованной форме позволяет произвести его разделение на отдельные составляющие: знак числа 
, мантиссу 
, знак порядка , порядок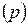 
, что позволяет удобно хранить и обрабатывать числа в компьютере.
Формат записи (1) называется также формой записи числа с порядком основания системы счисления или нормализованной экспоненциальной записью.
В компьютерных программах при записи чисел в десятичной системе счисления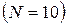 
экспоненциальная запись имеет вид:
 
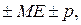
| (2) |
где - мантисса, 
- буква “Е”, заменяющая выражение “умножить на десять в степени …”).
В программировании при записи неотрицательного порядка числа применяется символ “+”, также используются ведущие нули, а в качестве десятичного разделителя не запятая, а точка. Корме того для улучшения читаемость программного кода иногда прописную букву заменяют строчной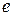 
.
Пример.
Рассмотрим алгебраическую запись одних и тех же десятичных чисел в естественной, алгебраической и нормализованной записи.
| Запись числа в естественной форме (“с фиксированной запятой”) | Запись числа в нормализованной форме (“с плавающей запятой”) | “Компьютерная” запись числа |
| 
| 
|
| 
| 
|
| 
| 
|
|
|
|
|
|
|
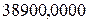
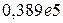
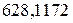
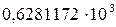
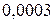
