 |
Измерения для интервальных переменных
|
|
|
|
Интервальные данные, безусловно, предоставляют нам наиболее полную информацию, включая категоризацию, ранжирование и установление интервалов. Интервальные значения могут быть подвержены любым арифметическим манипуляциям. Следовательно, приступая к исчислению средней тенденции и дисперсии для интервальных данных, мы можем и должны принять эту информацию о дополнительных возможностях во внимание.
Главной единицей для интервальных данных является среднее геометрическое, определяющее место средней точки в распределении с позиций как количества признаков от каждого конца распределения до этой точки, так и расстояние между ней и каждым признаком. Среднее геометрическое распределения – это то, что многие люди обычно связывают с термином “среднее арифметическое”. [c.401]
Давайте проиллюстрируем нахождение среднего геометрического на примере рис. 14.2. Если все признаки распределения имеют равные веса, и если они расположены на оси на равных интервалах так, что признаки с предельными значениями наиболее удалены от средней точки в том или ином направлении, а случаи с равными значениями расположены на равноудаленных точках оси, то точка среднего геометрического будет расположена в центре оси, где сумма значений и интервалов одной стороны уравновешивается суммой значений и интервалов другой. Как ясно из рисунка, и веса (количество признаков) и интервалы (крайние значения) важны для определения среднего геометрического.
Среднее геометрическое распределения, обозначаемое 
, вычисляется по следующей формуле:
,
где Xi – значение каждого отдельного случая;
N – количество случаев;
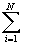– знак суммы всех отдельных случаев от 1 до N.
|
|
|
Обратите внимание, что в подсчете используются сложение и деление, два арифметических действия, произведенные с самими значениями (что принципиально отлично от просто количества случаев с данным значением) с подсчетом как всех значений, так и интервалов. Это и есть те манипуляционные возможности, которые отличают интервальные данные от данных более низких уровней измерения.
Заметьте, однако, еще, что, как видно из рис. 14.2г, именно потому, что среднее геометрическое чувствительно к величине интервалов, оно зависит от кренов в распределении, которые вызываются наличием одного или нескольких предельных признаков. Иными словами, небольшое количество случаев с предельными значениями может сделать значение среднего геометрического меньше или больше, чем реально репрезентативное. Давайте посмотрим, как это может получиться. [c.402]
Возьмем группу из 11 человек, 10 из которых зарабатывают 10.000 долларов в год, а один – 1 млн. Значение среднего геометрического дохода для этой группы – 100.000 долларов.
Но 10 из 11 членов группы зарабатывают, по сути дела, десятую часть этого количества. Таким образом, среднее геометрическое, хотя и точно подсчитанное, тем не менее не так репрезентативно, как, скажем, медиана, которая в другом случае равна 10.000 долларов. Вообще говоря, статистические процедуры с меньшими возможностями (предназначенные для более низких уровней измерения) всегда можно использовать в анализе данных, и, хотя они теряют некоторую информацию (например, расстояние до предельного значения, как здесь), иногда с их помощью можно получить более значимые результаты. Поспешим отметить, однако, что обратное неверно; статистические процедуры с высоким уровнем возможностей не имеют ни малейшей ценности для шкал низких уровней.
Наиболее часто употребляемый способ измерения дисперсии для интервальных данных, стандартное отклонение, из всех видов статистических процедур, которые мы используем, вероятно, один из интереснейших. На первый взгляд может показаться, что если мы хотим определить, насколько по отношению к распределению в целом типично среднее геометрическое, то все, что нужно сделать, – это измерить расстояние от его точки до каждого случая, сложить их и разделить на количество случаев N. Иными словами, мы подсчитаем среднее геометрическое расстояний вокруг среднего геометрического распределения по формуле:
|
|
|
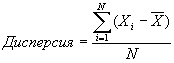
Чем больше дисперсия для данного распределения, тем менее типично среднее геометрическое, и, чем меньше дисперсия, тем более типично среднее геометрическое. [c.403]
Но если мы попробуем сделать все это на примере, скажем, рис. 14.2в, возникнут некоторые проблемы. Применив формулу к этому случаю, мы получим:
Даже в случае распределения с таким сильным отклонением, как в примере с доходами, мы получим:
И в любом случае среднего геометрического для любого распределения результат будет тот же. Причина проста. Мы, по сути дела, определили среднее геометрическое как такую точку, где все веса и интервалы уравновешены, точку или значение, относительно которых все остальное сбалансировано. Следовательно, при подсчете среднего геометрического вряд ли стоит удивляться, что мы получим [c.404] как раз то, что предполагалось. Тем не менее искушение измерить дисперсию путем измерения близости признаков к или удаления их от среднего геометрического сохраняет свою притягательность. Введем понятие стандартного отклонения.
Стандартное отклонение (s) является тем математическим инструментом, который может помочь выполнить вашу задачу. По сути дела, это процедура, которая сводит на нет свойства разнонаправленных интервалов уравновешивать друг друга путем простого возведения в квадрат утих интервалов (и избавляясь таким образом от отрицательных значений), измерения разброса квадратов интервалов вокруг среднего геометрического и затем извлечения из результата квадратного корня, с тем чтобы вернуться к начальным единицам интервалов. Формула, по которой все это вычисляется, напоминает прежнюю, акромe возведения в квадрат и извлечения квадратного корня. Формула эта такова:
|
|
|
где Xi – значение каждого отдельного случая;
– среднее геометрическое;
N – количество случаев;
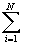– знак суммы всех отдельных случаев от 1 до N.
Таким образом, для примера на рис. 14.2в
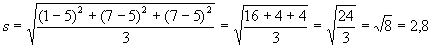
Она выражена в тех же единицах, что и исходные данные. Если переменные измеряются в одних и тех же или единицах, то стандартное отклонение может основой для выяснения репрезентативности средних геометрических; чем больше стандартное отклонение, ее репрезентативно среднее геометрическое. Но если единицы принципиально отличны или если анализируется одна переменная, интерпретация стандартного отклонения уже не столь проста.
Существует одно исключение из этого: переменные, чье [c.405] распределение близко к нормальному, т.е. такие, у которых существует единственная мода в самом центре распределения, а частоты симметрично убывают по направлениям к предельным значениям (графическое изображение нормального распределения, с которым вы, наверно, хорошо знакомы, – это просто колоколообразная кривая). Известно (из рассуждений, которые не входят в рамки нашего разговора), что в таких случаях 68,3% всех случаев лежат в пределах одного стандартного отклонения, от среднего геометрического ( ± s), 95,5% – в пределах двух стандартных отклонений от среднего геометрического ( ± 2 s) и 99,7% – в пределах трех стандартных отклонений от среднего геометрического ( ± 3 s). Фактически в случае таких распределений мы для любой точки можем определить, на сколько стандартных отклонений ниже или выше среднего геометрического она находится, и затем использовать эту информацию для выяснения относительного положения двух признаков в одной переменной или, наоборот, относительного значения двух переменных для одного и того же признака. Позволяет это сделать нам стандартная оценка, (z), которая вычисляется по следующей формуле:
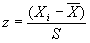
Представьте, что мы располагаем данными, например, по затратам на образование на душу населения в каждом штате, количеству работающих преподавателей на 1000 студентов в каждом штате и количеству награжденных выпускников средней школы на 100.000 населения в каждом штате в определенном году и что значения этих переменных по штатам распределяются по кривой, близкой к нормальной. Представьте затем, что мы хотим использовать эти данные для изучения политики в области образования в Аризоне и Виргинии. Мы сначала подсчитаем среднее геометрическое () и стандартное отклонение (s) для каждой переменной по всем 50 штатам, затем определим соответствующие стандартные оценки (z) для каждой переменной по двум нужным нам штатам. Результатом будут два набора значений в стандартных единицах (уже не в долларах, количестве учителей и документов, а в количестве стандартных отклонений от среднего [c.406] геометрического), которые могут быть использованы для определения индексов политики в области образования, для выяснения относительной позиции Аризоны и Виргинии среди других штатов или для стандартизации при необходимости cравнения принципиально отличных измерений. Таким образом, при использовании стандартного подсчета стандартное отклонение может оказаться очень полезным. [c.407]
|
|
|
ЗАКЛЮЧЕНИЕ
В этой главе мы остановились на статистических процедурах, которые описывают распределения в рамках одной переменной. Поскольку эта статистика характеризует отдельные переменные, ее часто называют одномерной. Мы видели, что различные одномерные статистические процедуры подходят для переменных различного уровня измерений – номинального, порядкового и интервального. В следующей главе мы рассмотрим двумерную статистику, т.е. такую, которая включает взаимосвязи двух переменных. [c.407]
Дополнительная литература
Если вы захотите глубже изучить статистику, см. литературу к гл. 16. Сейчас же будет полезнее начать с книг, которые облегчат применение диагностики и помогут овладеть некоторыми основными ее принципами. Мы предлагаем классическую и, вместе с тем, веселую кн.: Darrel H. How to Lie with Statistics. – N.Y.: Norton, 1954. Даррел определяет статистику как “статистикуляцию”. Гораздо более полное и легко читающееся издание по статистике: Schutte J.G. Everything You Always Wanted to Know About Elementary Statistics (but were afraid to Englewood Cliffs (NJ.): Prentice-Hall, 1977. [c.407]
|
|
|
