 |
Постановка линейной целочисленной задачи
|
|
|
|
Содержание
Введение
1. Постановка линейной целочисленной задачи
2. Теоретические основы методов отсечения
3. Первый алгоритм Гомори
4. Второй алгоритм Гомори
5. Алгоритм Дальтона и Ллевелина
6. Алгоритм Данцига
7. Некоторые выводы
Заключение
Список литературы
Приложение
Введение
Среди практически важных задач отыскания условного экстремума линейной функции важное место занимают задачи с требованием целочисленности всех (части) переменных. Они получили название задач целочисленного (частично целочисленного) программирования.
Исторически первой задачей целочисленного типа является опубликованная венгерским математиком Е. Эгервари в 1932 г. задача о назначении персонала.
Существуют различные методы решения таких задач, и заметное место среди них занимают методы отсечения. Рассмотрим в этой работе некоторые из методов отсечения, предварительно более подробно разобравшись с постановкой линейных целочисленных задач.
Постановка линейной целочисленной задачи
Среди совокупности п неделимых предметов, каждый i-и (i=1,2,…, п) из которых обладает по i-й характеристике показателем  и полезностью
и полезностью  найти такой набор, который позволяет максимизировать эффективность использования ресурсов величины
найти такой набор, который позволяет максимизировать эффективность использования ресурсов величины 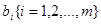 .
.
Математическая модель этой задачи может быть представлена следующим образом:
в области, определенной условиями
 (1)
(1)
 (2)
(2)
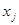 - целые,
- целые,  . (3)
. (3)
найти решение  при котором максимизируется (минимизируется) значение целевой функции
при котором максимизируется (минимизируется) значение целевой функции
 (4)
(4)
|
|
|
Если  ,то (1–4) является моделью задачи целочисленного программирования, если
,то (1–4) является моделью задачи целочисленного программирования, если 
 - моделью задачи частично целочисленного программирования.
- моделью задачи частично целочисленного программирования.
Частным случаем задачи целочисленного программирования является задача с булевыми переменными. Ее математическая модель в общем виде записывается следующим образом:
в области, определенной условиями
 (5)
(5)
 (6)
(6)
найти решение  , при котором максимизируется (минимизируется) значение функции
, при котором максимизируется (минимизируется) значение функции
 (7)
(7)
К классу задач целочисленного программирования примыкают задачи, в которых условие целочисленности всех или части переменных заменено требованием дискретности. А именно, для каждой j-и переменной  заранее определен набор значений (не обязательно целых), которые она может принимать:
заранее определен набор значений (не обязательно целых), которые она может принимать:  где
где  .
.
Предполагается, что  ранжированы, т.е.
ранжированы, т.е.  . Математическая модель общей задачи дискретного программирования может быть представлена следующим образом:
. Математическая модель общей задачи дискретного программирования может быть представлена следующим образом:
в области, определенной условиями
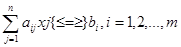 (8)
(8)
 (9)
(9)
найти решение  , при котором максимизируется (минимизируется) линейная функция
, при котором максимизируется (минимизируется) линейная функция
 (10)
(10)
Условие (9) определило название этого класса; задач. Если  ,то (8–10) называется задачей дискретного программирования; если
,то (8–10) называется задачей дискретного программирования; если  , то (8–10) называется задачей частично дискретного программирования.
, то (8–10) называется задачей частично дискретного программирования.
Нетрудно видеть, что условие (2–3) задачи (1–4) и условие (6) задачи (5–7) являются частным случаем условия (9) задачи (8–10). Действительно, (2–3) соответствует тому случаю, когда  для
для  . Условие (9) соответствует случаю, когда
. Условие (9) соответствует случаю, когда  .
.
Для задач целочисленного типа определено понятие допустимого и оптимального решения.
Вектор  , удовлетворяющий условиям (1–3) (соответственно (8–9)), называется допустимым решением задачи (1–4) (соответственно (8–10)). Допустимое решение, при котором функция (4) (соответственно (10)) достигает наибольшего (наименьшего) значения, называется оптимальным решением.
, удовлетворяющий условиям (1–3) (соответственно (8–9)), называется допустимым решением задачи (1–4) (соответственно (8–10)). Допустимое решение, при котором функция (4) (соответственно (10)) достигает наибольшего (наименьшего) значения, называется оптимальным решением.
|
|
|
Определив понятие допустимого и оптимального решения, естественно поставить вопрос об их нахождении. Казалось бы, что естественный путь решения целочисленной задачи состоит в решении соответствующей линейной задачи с последующим округлением компонент ее оптимального плана до ближайших целых чисел. На самом деле такой путь в большинстве случаев не только уводит, от оптимума, но даже приводит иногда к недопустимому решению задачи.
ПРИМЕР. В области, определенной условиями

 – целые
– целые
найти максимум функции  .
.
Решим задачу геометрически (рис. 1). Область поиска экстремума – многоугольник ODABC, но так как линия уровня целевой функции параллельна стороне АВ многоугольника, экстремум достигается в вершинах  и
и  , а также в любой точке отрезка АВ, и равен 7.
, а также в любой точке отрезка АВ, и равен 7.

(рис. 1)
Однако нас интересуют лишь точки с целочисленными координатами, следовательно, ни А, ни Вне являются допустимым решением задачи. Округляя значение координат А, получим  Но точка А' не принадлежит области поиска. Можно показать, что целочисленный оптимум достигается в точках N (3; 2) и M (2; 3) и равен 5. Обе точки внутри области поиска.
Но точка А' не принадлежит области поиска. Можно показать, что целочисленный оптимум достигается в точках N (3; 2) и M (2; 3) и равен 5. Обе точки внутри области поиска.
Построенный нами пример показал, что для решения задач с требованием целочисленности необходимо рассмотреть особые методы оптимизации; и, кроме того, мы видим, что оптимальное решение задач целочисленного программирования не обязательно принадлежит границе многогранника (многоугольника) условий, что было характерно для задач линейного программирования.
|
|
|


