 |
Алгоритм Дальтона и Ллевелина
|
|
|
|
Второй алгоритм Гомори имеет дело с частично целочисленными задачами линейного программирования. Дальтон и Ллевелин рассматривают 0 олее широкий класс задач – частично дискретные задачи линейного программирования и применительно к ним модифицируют второй алгоритм Гомори.
Напомним, что решением задачи дискретного программирования будем называть вектор, координаты которого принадлежат £ц области вида:
 (27)
(27)
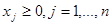 (28)
(28)
 (29)
(29)
и максимизирует значение функции


 (30)
(30)
Будем предполагать, что 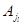 проранжированы, т.е.
проранжированы, т.е.  и являются наперед заданными числами.
и являются наперед заданными числами.
Теорема. Пусть x(£k, C) – оптимальное решение задачи (27–28, 30),  – элементы симплексной таблицы, соответствующей ему.
– элементы симплексной таблицы, соответствующей ему.
Если x(£k, C) является недопустимым решением задачи (27–30) и  , тогда, используя i-ю строку симплексной таблицы, можно построить отсечение, обладающее свойством правильности по формулам:
, тогда, используя i-ю строку симплексной таблицы, можно построить отсечение, обладающее свойством правильности по формулам:
 (31)
(31)
 (32)
(32)
где

 (33)
(33)
Доказательство. Проверим вначале условие отсечения. Пусть в оптимальном решении x(£k, C) координата  не удовлетворяет условию (29). Покажем, что в этом случае вектор х(£k, C) не удовлетворяет условиям (31, 32). Поскольку Nk – множество индексов небазисных переменных xi , которые в оптимальном решении равны нулю, то равенство (31) принимает вид
не удовлетворяет условию (29). Покажем, что в этом случае вектор х(£k, C) не удовлетворяет условиям (31, 32). Поскольку Nk – множество индексов небазисных переменных xi , которые в оптимальном решении равны нулю, то равенство (31) принимает вид  и будет отрицательным согласно условию теоремы. Следовательно,
и будет отрицательным согласно условию теоремы. Следовательно, 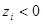 , т.е. условие отсечения не выполняется.
, т.е. условие отсечения не выполняется.
Проверим условие правильности. Для этого покажем, что любое допустимое решение задачи (27–30) удовлетворяет условиям (31, 32).
|
|
|
Запишем разложение для координаты допустимого решения задачи (27–30) по небазисным переменным
 (34)
(34)
и рассмотрим два случая: a)  ; б)
; б)  . Введем обозначения:
. Введем обозначения:

и представим (34) в виде

где

Очевидно,  так как
так как  .
.
Рассмотрим случай а): 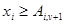 , или что все равно,
, или что все равно,  .
.
Отсюда  Но
Но 
 поэтому
поэтому
 (35)
(35)
Домножим обе части (35) на неотрицательную величину  и сложим с неотрицательной величиной
и сложим с неотрицательной величиной  :
:
 (36)
(36)
Рассмотрим случай б):  или, что все равно,
или, что все равно,  Так как по определению
Так как по определению  , то
, то  Умножим обе части неравенства
Умножим обе части неравенства  на неотрицательную величину
на неотрицательную величину  и на -1, получим
и на -1, получим  . Прибавляя к полученному выражению неравенство
. Прибавляя к полученному выражению неравенство  , получим
, получим
 (37)
(37)
Таким образом, в а) и в б) случаях пришли к одному и тому же неравенству (36) и (37). Пользуясь ранее введенными обозначениями, их можно записать
 (38)
(38)
Формула (38) определяет правильные отсечения. Сравнивая ее с выражением (31–32), приходим к выводу, что коэффициенты  определяются следующим образом:
определяются следующим образом:

Теорема доказана.
Алгоритм Дальтона – Ллевелина может быть описан следующим образом.
1. Решается (£k, C) – задача (27–30) (вначале k = 0). Пусть x(£k, C), k = 0, 1, 2,… оптимальное решение (£k, C) – задачи,  – симплексная таблица.
– симплексная таблица.
2. Проверяется условие допустимости по всем координатам оптимального вектора решения х(£k, C) (£k, C) – задачи. Если условие допустимости выполняется, то полученное решение является оптимальным решением исходной задачи (27–30). Если условие допустимости не выполняется хотя бы по одной координате, осуществляется переход к 3.
3. Пусть  не удовлетворяет условию допустимости. Тогда выбирается
не удовлетворяет условию допустимости. Тогда выбирается
i 0 = min { i | 1< i < n 1, х j 0 k – не удовлетворяет (29)}.
4. Для выбранного номера i = i 0 строится правильное отсечение, т.е. вводится дополнительная переменная
|
|
|

где  определяется формулой (33),
определяется формулой (33),
5. Добавляем линейное ограничение, определяющее правильное отсечение, к условиям (£k, C) – задачи и получаем новую (£k+1, C) – задачу. Полагая k = k + 1, переходим к п. 1.
Приведем без доказательства теорему о конечности алгоритма.
Теорема. Если: коэффициенты целевой функции дискретны; F (x) ограничена снизу на многогранном множестве £; задача (£, C) имеет по крайней мере одно решение; выбор строки для построения правильного отсечения производится по правилу минимального номера и (£k, C) – задачи решаются методом последовательного уточнения оценок, то алгоритм Дальтона и Ллевелина сходится.
Алгоритм Данцига
Способ построения правильных отсекающих плоскостей, предложенный Данцигом значительно проще, чем все изложенные выше способы. Но, как показали Гомори и Гофман, конечность алгоритма Данцига гарантируется лишь для очень узкого класса задач. На примере алгоритма Данцига видно, насколько тонким является вопрос о построении правильных отсечений и сколь осторожно следует подходить к различным упрощенным алгоритмам.
Рассматривается полностью целочисленная задача линейного программирования:
Максимизировать
 (39)
(39)
при условиях
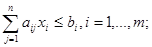 (40)
(40)
 (41)
(41)
 – целые,
– целые, 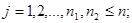 (42)
(42)
Ранг матрицы  считаем равным m.
считаем равным m.
Теорема. Пусть x(£r, C)=xr является оптимальным опорным планом задачи (£r, C) и xr не удовлетворяет условию целочисленности, Nr – множество индексов, нумерующих небазисные переменные, соответствующие xr.
Тогда неравенство
 (43)
(43)
является правильным отсечением.
Правильное отсечение, отсекающее нецелочисленный оптимум x(£r, C) задачи (£r, C ), можно записать следующим образом:

 – целое.
– целое.
Заметим, что каждая из вновь вводимых переменных  однозначно определяется заданием переменных
однозначно определяется заданием переменных  , так что
, так что  .
.
Обозначим через  упорядоченные в порядке возрастания компоненты
упорядоченные в порядке возрастания компоненты  плана x задачи (39) – (41), так что
плана x задачи (39) – (41), так что

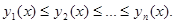 (44)
(44)
Положим
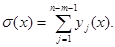 (45)
(45)
Лемма. Если для некоторого плана x задачи (39) – (41)
 , (46)
, (46)
|
|
|
то
 (47)
(47)
Доказательство проведем по индукции. Сначала докажем, что
 (47¢)
(47¢)
По определению
 (48)
(48)
Так как ранг матрицы  равен m, то
равен m, то
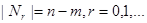
где 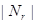 – число элементов множества
– число элементов множества  . Из определения чисел
. Из определения чисел  получаем
получаем
 (49)
(49)
 (50)
(50)
Из (48), (49), (50) и (46) имеем

Лемма доказана при р=1.
Теперь допустим, что лемма верна при  , и докажем ее при
, и докажем ее при  :
:

Лемма доказана.
Пользуясь леммой, докажем две теоремы.
Теорема 1. Если каждый оптимальный план задачи (39) – (42) содержит не менее (m +2) положительных компонент, то алгоритм Данцига не будет конечным.
Доказательство. Допустим, что на s-й итерации алгоритма Данцига получится искомый оптимальный план 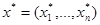 . Рассмотрим числа
. Рассмотрим числа
 (51)
(51)
Все они целые и среди них должно быть (n - m) нулей – это небазисные переменные 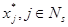 . Кроме того, по условию среди чисел
. Кроме того, по условию среди чисел  , должно быть по крайней мере (m +2) положительных числа, т.е. не больше чем (n - m - 2) нулей.
, должно быть по крайней мере (m +2) положительных числа, т.е. не больше чем (n - m - 2) нулей.
По определению чисел  отсюда следует, что
отсюда следует, что
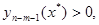
а так как  должно быть целым, то
должно быть целым, то
 (52)
(52)
Но по определению чисел 
 (53)
(53)
Из (52) получаем
 (54)
(54)
и по лемме
 (55)
(55)
Из (52), (53) и (55) следует, что среди чисел (51) по крайней мере [1+(m +1)+ s ] = [ m +2+ s ] положительных, а следовательно, не больше чем [ n + s – (m +2+ s)] = (n - m - 2) нулей. Но выше было отмечено, что среди чисел (51) должно быть (n - m) нулей. Получилось противоречие. Теорема 1 доказана.
Следствие (из теоремы 1). Для того чтобы алгоритм Данцига был конечным, необходимо, чтобы искомый оптимальный план лежал на ребре многогранного множества (40) – (41) (предполагается, что задача (39) – (41) невырожденная).
Хотя это условие и является весьма жестким, ему удовлетворяют, например, все (невырожденные) задачи следующего вида.
Максимизировать
 (56)
(56)
при условиях
 (57)
(57)
 (58)
(58)
 (59)
(59)
|
|
|
 – целое,
– целое, 

 (60)
(60)
А это важный класс задач.
Однако приведенное в следствии необходимое условие конечности алгоритма Данцига не является достаточным. Действительно, имеет место следующая
Теорема 2. Если для некоторого оптимального плана x' задачи (39) – (42) и некоторого плана x» задачи (39) – (41) имеют место неравенства
 (61)
(61)
и
 (62)
(62)
то алгоритм Данцига не будет конечным.
Доказательство. Допустим, что алгоритм Данцига конечен. Тогда из (61) следует, что точка x» была отсечена на некоторой (скажем, р -й) итерации, так что
 (63)
(63)
Но из (62) и леммы получим
 (64)
(64)
Сравнивая (63) и (64), получаем противоречие. Теорема 2 доказана.
Итак, упрощенный алгоритм Данцига будет конечным лишь в весьма редких случаях.
Некоторые выводы
Попробуем охарактеризовать поведение алгоритмов метода отсечения при решении задач целочисленного линейного программирования. В качестве меры продолжительности вычислений могут рассматриваться количество симплексных итераций I и количество правильных отсечений (дополнительных линейных ограничений) D.
Для первого алгоритма Гомори и различных его обобщений I и D также тесно связаны между собой (как показывает эксперимент, в большинстве случаев решение отдельной задачи (£, С) требует сравнительно небольшого количества симплексных итераций).
Переходим к изложению отдельных свойств алгоритмов метода отсечения.
Числа I и D имеют (в среднем) тенденцию к возрастанию с увеличением числа переменных и ограничений, ростом порядка коэффициентов задачи и увеличением заполненности матрицы  .
.
Это явление кажется естественным, но опыт показывает, что в дискретном программировании «естественное» и «правдоподобное» не всегда оказывается правильным. Точнее говоря, опыт, накопленный на задачах ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ, нельзя механически переносить на задачи ЦЕЛОЧИСЛЕННОГО ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ.
Прежде всего, обращает на себя внимание «нерегулярность», «непредсказуемость» поведения алгоритмов метода отсечения. Для ряда задач оптимальное решение не удавалось получить после многих тысяч итераций, в то время как другие задачи решались за несколько десятков итераций.
Не удается установить непосредственную связь между размерами задач (т.е. числом ограничений m и переменных n) и числом итераций: неудачи были зафиксированы даже для небольших задач (m≤10, n≤10), а успехи – для задач достаточно большого размера (m = 215, n = 2600). Возможно, впрочем, что попытка установления подобной связи – это неправомерное перенесение результатов ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ в область ЦЕЛОЧИСЛЕННОГО ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ.
|
|
|
Быть может, более естественной характеристикой задачи (£, С) является не число m линейных ограничений, задающих многогранное множество £, а число m ц - линейных ограничений, задающих многогранное множество V(£)*). Между тем легко привести примеры, когда при небольших m и n число mц будет достаточно велико.
«Нерегулярность» сказывается и в следующем факте, подмеченном рядом исследователей: иногда удается существенно сократить число итераций за счет перенумерации переменных.
Наконец, имеет место немонотонность приближения псевдоплана Хr к оптимальному плану X* – с ростом r расстояние ρ(Хr, X*) не обязательно уменьшается и лишь на последней итерации обязательно становится равным нулю.
Большое влияние на число итераций оказывает правило выбора порождающей строки. Здесь также имеет место «нерегулярность» – в то время как одно правило приводит к успеху за десятки итераций, другое не дает решения после тысяч итераций.
При решении задач целочисленного линейного программирования по методу отсечения имеются как успехи, так и неудачи.
К наиболее успешным работам следует отнести:
1) Задачи покрытия, в том числе задачи, связанные с минимизацией булевых функций.
2) Применение к задачам оптимального кодирования.
3) Применение к задаче оптимального извлечения информации из параллельных систем памяти.
Наиболее характерными задачами, для которых имела место неудача, являются:
1) Задачи коммивояжера.
2) Задача теории расписаний.
3) Некоторые из обобщенных задач покрытия.
В настоящий момент отсутствует исчерпывающее объяснение удач или неудач различных вычислительных экспериментов. Все же для задачи коммивояжера и задачи теории расписаний является правдоподобным следующее соображение.
Формулировка этих задач на языке ЦЕЛОЧИСЛЕННОГО ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ является «неестественной». Для задачи сравнительно небольшой в «естественной» формулировке, в модели ЦЕЛОЧИСЛЕННОГО ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ фигурирует большое количество ограничений и переменных. Возможно, что для этих задач более перспективными являются комбинаторные методы (например, метод ветвей и границ для задачи коммивояжера). Впрочем, последнее утверждение является спорным, так как комбинаторные методы очень чувствительны к специфике задач, введению дополнительных условий и т.п.
По-видимому, успех в решении задач покрытия связан с тем, что удалось напасть на класс задач, практически важных и в то же время успешно решаемых. Было бы весьма интересно точно охарактеризовать класс задач покрытия, хорошо решаемых по методу отсечения. Это тем более интересно, что построены примеры обобщенных задач покрытия, для которых возникают значительные вычислительные трудности.
И вообще, выделение отдельных классов эффективно решаемых задач – важная и интересная проблема.
Заключение
Подведем некоторые итоги. Метод отсечения находится в стадии развития и совершенствования. При реализации этого метода возникают трудности, носящие, по-видимому, не только технический, но и принципиальный характер. В настоящий момент можно говорить о решении с помощью метода отсечения задач не более чем среднего размера (сотни переменных и десятки ограничений).
Наиболее перспективными для дальнейших исследований по методу отсечения представляются следующие направления:
1) Исследование строения множеств £ц и V(£ц).
2) Исследование свойств правильных отсечений.
3) Указание новых способов построения правильных отсечений.
4) Развитие новых классов алгоритмов метода отсечения (например, прямых алгоритмов).
5) Выделение отдельных классов эффективно решаемых задач.
Список литературы
1. Корбут А.А., Финкельштейн Ю.Ю. Дискретное программирование, М.: Наука, – 1969.
2. Лященко И.Н. Линейное и нелинейное программирование, М.: Наука, – 1985.
3. Санович К.М. Исследование операций, М.: Наука, – 1989.
Приложение
1. ПРОГРАММА, РЕАЛИЗУЮЩАЯ ПЕРВЫЙ АЛГОРИТМ ГОМОРИ
#include<ctype.h>
#include<string.h>
#include<conio.h>
#include<stdio.h>
#include<math.h>
#include<stdlib.h>
class simplex {int n; // число переменных +1
int m; // число ограничений
int *basis;
int *mi;
float *mc;
int flag;
public:simplex (int m1, FILE *fp, int f);
~simplex()
{if(mi) free(mi);
if(mc) free(mc);
if(basis) free(basis);
}
void printsimtable (int g);
void iterac();
void resultat();
};
simplex:simplex (int m1, FILE *fp, int f)
{FILE *fp1;
int fl, i;
if((fp1=fopen («hell1», «w+»))==NULL) {printf («Ошибка выделения памяти!»);
exit(1);
};
m=m1;
n=0;
basis=NULL;
flag=f;
fl=1;
do {fread(&c, sizeof (struct koef), 1, fp);
if (! feof(fp))
{do {fread(&i, sizeof(int), 1, fp1);
if (! feof(fp1) && i==c.ind)
{fl=0;
break;
}
} while (! feof(fp1));
if(fl) {fwrite (&c.ind, sizeof(int), 1, fp1);
n++;
fflush(fp1);
}
else fl=1;
rewind(fp1);
}
} while (! feof(fp));
rewind(fp);
if (m>n-1) {printf («Число ограничений больше или равно числу переменных»);
getch();
exit(1);
}
mi=(int *) malloc (sizeof(int)*n);
mc=(float *) malloc (sizeof(float)*n*(m+1));
if (! mc ||! mi) {printf («Ошибка выделения памяти!»);
getch();
exit(1);
}
fread (mi, sizeof(int), n, fp1);
qsort (mi, n, sizeof(int), sort);
fclose(fp1);
remove («hell1»);
for (fl=0; fl<m+1; fl++)
for (i=0; i<n; i++)
*(mc+fl*n+i)=0;
fl=m;
do {fread(&c, sizeof (struct koef), 1, fp);
if (! feof(fp))
{if (c.ind)
{for (i=1; i<n; i++)
if (c.ind==*(mi+i))
{*(mc+fl*n+i)=*(mc+fl*n+i)+c.coef;
break;
}
}
else{*(mc+fl*n)=c.coef;
if (fl==m) fl=0;
else fl++;
}
}
} while (! feof(fp));
}
void simplex:iterac()
{int i, j, fl, fl1, k, l;
float s, min;
for (i=1; i<n; i++)
{if(*(mc+m*n+i)!=0)
{fl=1;
for (j=0; j<m; j++)
if(*(mc+j*n+i)!=0) {fl=0;
break;
}
if(fl) {printf («Не все перменные целевой функции входят в ограничения»);
getch();
exit(1);
}
}
}
basis=(int *) malloc (sizeof(int)*m);
if(! basis) {printf («Ошибка выделения памяти»);
getch();
exit(1);
}
for (i=0; i<m; i++)
*(basis+i)=0;
i=0;
do
{fl=1;
fl1=0;
for (j=1; j<n; j++)
if(*(mc+i*n+j)>0) {fl=0;
break;
}
if(fl) {printf («Переменные должны быть положительны»);
getch();
exit(1);
}
s=*(mc+i*n+j);
for (l=0; l<n; l++)
*(mc+i*n+l)=*(mc+i*n+l)/s;
for (l=0; l<=m; l++)
if (l!=i) {s=*(mc+l*n+j);
for (k=0; k<n; k++)
*(mc+n*l+k)=*(mc+l*n+k) – s*(*(mc+i*n+k));
}
for (l=0; l<m; l++)
{s=0;
for (k=1; k<n; k++)
s=s+fabs(*(mc+l*n+k));
if (s==0) {if(*(mc+l*n)==0) printf («Уравнения линейно зависимы»);
else printf («Система ограничений несовместна»);
getch();
exit(1);
}
}
*(basis+i)=j;
for (l=0; l<m; l++)
if(*(mc+l*n)<0)
for (k=0; k<n; k++)
*(mc+l*n+k)= – (*(mc+l*n+k));
for (l=0; l<m; l++)
if((*(basis+l)==0)||(*(mc+l*n+(*(basis+l)))<0)) {i=l; fl1=1; break;}
} while(fl1);
printsimtable(0);
do {min=100000;
fl=0;
for (l=1; l<n; l++)
{if(*(mc+m*n+l)>0) {fl=1;
fl1=1;
for (k=0; k<m; k++)
if(*(mc+k*n+l)>0)
{fl1=0;
s=*(mc+k*n)/(*(mc+k*n+l));
if (s<min) {min=s;
i=k;
j=l;
}
}
if(fl1) {printf («Решения нет»);
getch();
exit(1);
}
break;
}
}
if(fl) {s=*(mc+i*n+j);
for (l=0; l<n; l++)
*(mc+i*n+l)=*(mc+i*n+l)/s;
for (l=0; l<=m; l++)
if (l!=i) {s=*(mc+l*n+j);
for (k=0; k<n; k++)
*(mc+l*n+k)=*(mc+l*n+k) – s*(*(mc+i*n+k));
}
printsimtable(0);
*(basis+i)=j;
}
} while(fl);
}
void simplex:resultat()
{int i, j, fl;
if (flag==-1) printf («Минимальное значение функции цели равно % 8.2f\n»,*(mc+m*n));
else printf («Максимальное значение функции цели равно % 8.2f\n», – (*(mc+m*n)));
printf («Оптимальный план:»);
for (i=1; i<n; i++)
{fl=0;
for (j=0; j<m; j++)
if(*(mi+i)==*(basis+j)) {fl=1;
break;
}
if(fl) printf («x % 02d=%-5.2f\n»,*(mi+i),*(mc+j*n));
else printf («x % 02d=0 \n»,*(mi+i));
printf(«»);
}
}
void simplex:printsimtable (int g)
{int i, j, k, v=g, raz;
clrscr();
raz=n-1–6*(v+1);
if((raz<=0)&&(abs(raz)<6)) raz=6+raz;
else if (raz>0) raz=6;
else return;
for (j=0; j<3; j++)
{if (j!=1) {printf(«* * *»);
for (i=0; i<raz; i++)
printf(» *»);
if (raz<6) printf («\n»);
}
else {if(*(mc+m*n)>=0) printf («* *%8.2f *»,*(mc+m*n));
else printf («* * -%-7.2f *», – (*(mc+m*n)));
for (i=1; i<=raz; i++)
if(*(mc+n*k+6*v+i)>=0) printf («%8.2f *»,*(mc+n*k+6*v+i));
else printf («-%-7.2f *», – (*(mc+n*k+6*v+i)));
if (raz<6) printf («\n»);
}
}
for (i=0; i<20+raz*10; i++)
printf(«*»);
getch();
rewind(fp);
simplex ob (no, fp, f);
gomori();
ob.iterac();
ob.resultat();
}
|
|
|


